- Неполное частное
- Содержание
- Определение
- Обозначения
- Связанные определения
- Свойства
- Число делителей
- Обобщения
- См. также
- Полезное
- Смотреть что такое «Неполное частное» в других словарях:
- Что такое частное в математике?
- Деление
- Наглядные примеры
- Проверка
- Полное и неполное частное
- Значение частного двух чисел в математике
- Что такое частное чисел
- Деление как операция
- Основные свойства деления
- Неполное частное
- Изменение частного в зависимости от изменения делимого и делителя
- Задачи, примеры вычисления частного
- Задача 1
- Задача 2
- Деление чисел с остатком
- Деление с остатком целых положительных чисел
- Деление с остатком положительного числа на целое отрицательное
- Деление с остатком целого отрицательного числа на целое положительное
- Деление с остатком целых отрицательных чисел
- Деление с остатком с помощью числового луча
- Проверка деления с остатком
- Теорема о делимости целых чисел с остатком
Неполное частное
Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.
Содержание
Определение
Если для некоторого целого числа a и целого числа 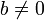
При этом число b называется делителем числа a , делимое a будет кратным числа b , а число q называется частным от деления a на b.
Обозначения
означает, что aделится наb
- b | a означает, что bделитa .
Связанные определения
- Натуральное число, имеющее ровно два натуральных делителя (единицу и само себя), называется простым. Все остальные числа (кроме единицы) называются составными.
- Собственным делителем числа называется всякий его делитель, отличный от самого числа. У простых чисел существует ровно один собственный делитель — единица.
- Вне зависимости от делимости целого числа a на целое число
, число a всегда можно разделить на b с остатком, то есть представить в виде: a = bq + r , где
.
В этом соотношении число r называется остатком (от деления a на b), а число q — неполным частным (от деления a на b). Число a делится нацело на b тогда и только тогда, когда остаток от деления a на b равен нулю.
Свойства
- Любое натуральное число является делителем нуля;
- Единица является делителем любого целого числа;
- Любое натуральное число является делителем самого себя.
Число делителей
Число положительных делителей натурального числа n обычно обозначается τ(n) , является мультипликативной функцией, для неё верна асимптотическая формула Дирихле:
Обобщения
Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.
См. также
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Неполное частное» в других словарях:
Дробь — Если делится какое нибудь целое число а на другое целое число b, т. е. ищется число x, удовлетворяющее условию bx=а, то могут представиться два случая: или в ряду целых чисел найдется число х, которое этому условию удовлетворит, или же окажется,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Деление с остатком — Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.… … Википедия
Остаток от деления — в арифметике один из результатов операции деления с остатком. Образуется, если результат деления не может быть выражен целым числом, при этом остаток от деления должен быть по абсолютной величине меньше делителя. В случае, если числа… … Википедия
Фундаментальные алгоритмы — Два основных фундаментальных алгоритма это алгоритм деления и алгоритм Евклида Алгоритм деления предназначен для вычисления неполного частного и остатка от деления двух целых чисел. Алгоритм деления a делимое b делитель q неполное частное r –… … Википедия
ГОРНЕРА СХЕМА — прием для нахождения неполного частного и остатка при делении многочлена на двучлен , где все коэффициенты лежат в нек ром поле, напр., в поле комплексных чисел. Всякий многочлен единственным способом представим в виде где есть неполное частное,… … Математическая энциклопедия
Целая часть — График функции «пол» (целая часть числа) … Википедия
Преобразование Гаусса — В математике, преобразование Гаусса (измеримая) динамическая система на отрезке [0,1], заданная отображением где обозначает дробную часть числа. Это преобразование «стирает» первое неполное частное в разложении числа в цепную дробь: Кроме… … Википедия
Единая сетевая разметка — (ЕСР) система цифрового обозначения железнодорожных станций на территории стран СНГ и Балтии. С помощью кодов ЕСР кодируются станции, открытые для выполнения грузовых операций, производящие перевалку грузов с железнодорожного на речной или… … Википедия
ЗНАНИЕ В АРАБО-МУСУЛЬМАНСКОЙ ФИЛОСОФИИ — ЗНАНИЕ В АРАБО МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. Благодаря слитости процессуального и субстанциального аспектов в категории масдара (отглагольного существительного) арабское языковое мышление имеет тенденцию рассматривать процесс и результат как нечто … Философская энциклопедия
ЗНАНИЕ В АРАБО-МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. — ЗНАНИЕ В АРАБО МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. Благодаря слитости процессуального и субстанциального аспектов в категории масдара (отглагольного существительного) арабское языковое мышление имеет тенденцию рассматривать процесс и результат как нечто… … Философская энциклопедия
Источник
Что такое частное в математике?
Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.
Деление
В математике есть четыре простейших операции:
Если мы говорим о частном, то нас будет интересовать такая операция, как деление.
Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:
- Двоеточие (:)
- Косая черта (/)
- Обелюс (тире между двумя точками ÷)
В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.
Частное рассказывает, во сколько раз одно число больше другого.
Наглядные примеры
Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.
Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:
a:b=c
Запишем простой пример из математики:
80:2=40
80 – делимое (оно делится)
2 – это делитель (на него разделяют)
Восемьдесят больше, чем сорок, в два раза.
Другой пример выглядит так:
120:2=60
Сто двадцать больше, чем шестьдесят, в два раза.
Проверка
Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:
Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.
Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.
Полное и неполное частное
В результате проведения математических подсчетов частное может быть двух видов:
- Полное. В результате деления мы получаем целое число:
100:2=50
50 – полное частное
- Неполное. Если в результате мы получаем остаток:
51:2=25 (остаток 1)
25 – неполное частное
1 – остаток от деления
Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:
30:6=x
Чтобы найти частное, следует делимое разделить на делитель:
Ответ 5 – это частное в данном примере.
Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.
Источник
Значение частного двух чисел в математике
Что такое частное чисел
Частное чисел – это результат деления одного числа на другое. Оно показывает, сколько раз число a содержится в числе b.
Деление как операция
Деление – арифметическая операция, обратная умножению, суть которой заключается в нахождении одного из сомножителей по произведению и другому множителю. В данном случае произведение переходит в делимое, имеющийся сомножитель – в делитель, искомый сомножитель – в частное.
Подобно тому, как неоднократно прибавить число – это значит умножить, так и неоднократно вычесть – это значит разделить.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На письме данную операцию можно обозначать разными символами:
- : двоеточием;
- ÷ обелюсом;
- / косой чертой (слеш);
- — горизонтальной чертой (знак дроби).
Процесс деления имеет следующий вид:
В цифрах данное выражение можно записать так:
Основные свойства деления
Деление не коммутативно, то есть не перестановочно – от перемены мест элементов операции частное изменяется:
Деление не ассоциативно – то есть при последовательном выполнении деления трех или более чисел последовательность операций имеет значение, при смене порядка выполнения изменится результат:
Деление дистрибутивно справа – на одном и том же множестве две бинарные операции имеют свойство согласованности:
\((a + b): x = (a : x)+(b : x);\)
Имеется единственный нейтральный элемент – число 1, при делении на единицу результатом является исходное число (делимое):
Имеется единственный обратный элемент – число 1, при делении единицы на число результатом является число, обратное исходному (делителю):
Существует единственный нулевой элемент – число 0, при делении нуля на любое число результатом будет нуль:
Деление на нулевой элемент не определено:
Деление на противоположный элемент дает минус единицу:
Неполное частное
Неполное частное – результат, который получился после деления с остатком.
Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.
Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.
Например, 17 не делится без остатка на 5.
Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.
Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.
Изменение частного в зависимости от изменения делимого и делителя
- увеличение делимого в несколько раз приведет к тому, что частное увеличится во столько же раз:
- уменьшение делимого в несколько раз приведет к тому, что частное уменьшится во столько же раз:
- увеличение делителя в несколько раз приведет к тому, что частное уменьшится во столько же раз:
- уменьшение делителя в несколько раз приведет к тому, что частное увеличится во столько же раз:
Частное не изменится, если делимое и делить одновременно увеличить или уменьшить в одинаковое количество раз:
Задачи, примеры вычисления частного
Для того, чтобы проиллюстрировать данную арифметическую операцию, решим простые задачи.
Задача 1
В книге 891 страница. Она поделена на 9 равных глав. Узнайте, сколько страниц в одной главе.
Для этого количество страниц разделим на количество глав:
891 : 9 = 99 (страниц)
Ответ: 99 страниц.
Задача 2
У Антона есть 22 апельсина. Он хочет приготовить из них компот. Для одного литра компота ему понадобится 3 апельсина. Нужно вычислить, сколько литров напитка сможет приготовить Антон и сколько апельсинов у него останется.
Источник
Деление чисел с остатком
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка d = a − b * c.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы d = a − b * c.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Докажем возможность существования a = b * q + r .
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Если посчитать, что b — целое положительное число, тогда, следует выбрать целое q так, чтобы произведение b * q не было больше значения числа а , а произведение b * (q + 1) было больше, чем a.
Тогда необходимо взять q такое, чтобы данное неравенством b * q
Источник
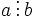 означает, что aделится наb
означает, что aделится наb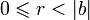 .
.