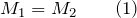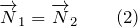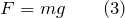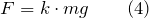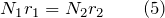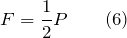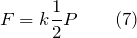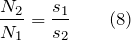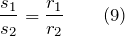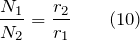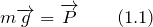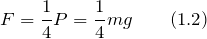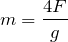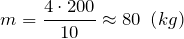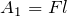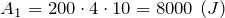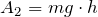Подвижный и неподвижный блок
Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.
Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
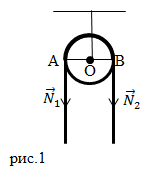
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
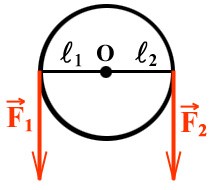
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:
так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.
Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
Комбинация неподвижных блоков
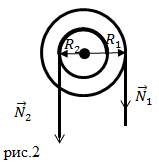
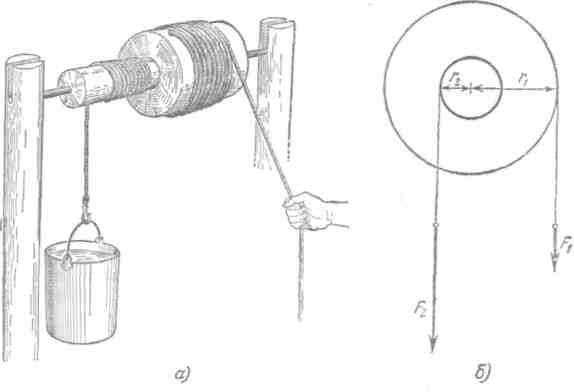
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.
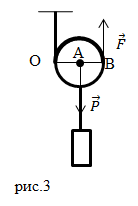
Условие равновесия для рычага на рис.2 станет формула:
Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы 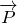
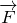
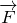
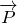
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где 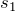
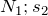
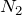
Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( 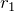
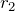
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы 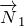
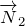
Примеры решения задач
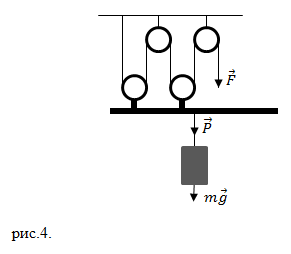
| Задание | Используя систему из двух подвижных и двух неподвижных блоков, рабочие поднимают строительные балки, при этом прикладывают силу равную 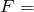 200 Н. Чему равна масса (m) балок? Трение в блоках не учитывайте. 200 Н. Чему равна масса (m) балок? Трение в блоках не учитывайте. |
| Решение | Сделаем рисунок. |
Вес груза, приложенный к системе грузов, будет равен силе тяжести, которая приложена к поднимаемому телу (балке):
Неподвижные блоки выигрыша в силе не дают. Каждый подвижный блок дает выигрыш в силе в два раза, следовательно, при наших условиях мы получим выигрыш в силе в четыре раза. Это значит, что можно записать:
Получаем, что масса балки равна:
Вычислим массу балки, примем 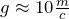
| Задание | Пусть высота, на которую поднимают балки рабочие, в первом примере равна 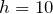 м. Чему равна работа, которую совершают рабочие? Какова работа груза по перемещению на заданную высоту? м. Чему равна работа, которую совершают рабочие? Какова работа груза по перемещению на заданную высоту? |
| Решение | В соответствии с «золотым правилом» механики, если мы, используя имеющуюся систему блоков, получили выигрыш в силе в четыре раза, то проигрыш в перемещении составит тоже четыре. В нашем примере это означает, что длина веревки (l) которую рабочим следует выбрать составит длину в четыре раза большую, чем расстояние, которое пройдет груз, то есть: |
Работа, которую совершат строители, равна:
Вычислим 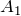
Работа груза (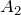
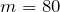
Вычислим 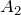
Источник
Простые механизмы. Блок.
Одним из простых механизмов является блок. Блок — это колесо с желобом, по которому пропущена веревка или трос. Используется блок, как и все простые механизмы, для преобразования силы — т.е. изменения направления и модуля приложенной силы.
Блоки бывают подвижные и неподвижные. Рассмотрим каждый случай подробно.
Неподвижный блок.
Неподвижный блок — это блок, ось которого (точка О на рисунке) закреплена, и блок при подъеме грузов не опускается и не поднимается.
Такой блок можно рассматривать как рычаг первого рода, у которого оба плеча равны между собой, и равны радиусу колеса блока:
Так как плечи рычага равны, то мы не получим выигрыша в силе. Проверим это, используя формулу равновесия рычага:
В нашем случае неподвижного блока:
Действительно, для того чтобы уравновесить силу на одном конце веревки, перекинутой через блок, нам необходимо приложить такую же силу на другом конце. Поэтому неподвижные блоки используют в том случае, если удобнее изменить направление силы, для совершения работы. Например, удобнее поднимать груз, удерживая веревку при помощи своего веса, поэтому на рисунке экспериментатор использует неподвижный блок.
Используя комбинации из неподвижных блоков можно менять направление силы как угодно:
И в этом случае, используя уже два неподвижных блока — мы не получаем выигрыша в силе, зато изменили направление приложения силы, теперь для поднятия груза силу мы должны приложить в горизонтальном направлении.
Подвижный блок
Подвижный блок — это блок, ось которого не закреплена, а поднимается вместе с грузом. Изобразим подвижный блок находящийся в равновесии, отметим на рисунке силы, действующие на систему, а также плечи приложения этих сил:
Подвижный блок можно сравнить с рычагом второго рода. Действительно: точка опоры О лежит по одну сторону от точки приложения сил, отрезок ОА — плечо силы P
Источник
Неподвижный блок
Вы будете перенаправлены на Автор24
Блок представляет собой устройство, которое состоит из колеса с желобом, по которому пропускают, трос, веревку или цепь, а также прикрепленной к оси колеса обоймы с крюком. Блок может быть неподвижным и подвижным. У неподвижного блока ось закреплена, и она не двигается при подъеме или опускании груза.
Рисунок 1. Неподвижный блок
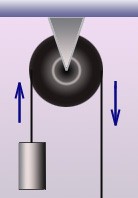
Неподвижный блок помогает изменить направление действия силы. Перекинув через такой блок, подвешенный вверху, веревку, мы можем, поднимать груз вверх, сами при этом находясь внизу.
Рисунок 2. Применение неподвижного блока для подъёма грузов
Однако выигрыша в силе применение неподвижного блока нам не дает. Мы можем представить блок в виде рычага, вращающегося вокруг неподвижной опоры — оси блока. Тогда радиус блока будет равен плечам, приложенных с двух сторон сил, — силы тяги нашей веревки с грузом с одной стороны и силы тяжести груза с другой. Плечи будут равны, соответственно, выигрыша в силе нет.
Рисунок 3. Неподвижный блок как равноплечий рычаг
На практике неподвижные блоки используют в системах, сочетающих их с другими блоками. или рычагами. Например, двойной блок из двух неподвижных блоков различного диаметра, насаженных на общую ось, позволяет не только изменить направление приложения силы, но и обеспечить выигрыш в силе или скорости.
Рисунок 4. Двойной блок и его схема
Ворот, применяемый в колодцах для подъёма воды, или кабестан, с помощью которого раньше поднимали якорь на кораблях — представляют собой комбинацию неподвижного блока с рычагом.
Рисунок 5. Кабестан (вертикальный ворот)
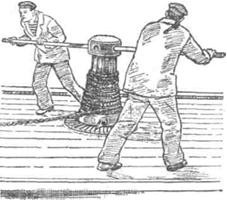
Пожарные, альпинисты, маляры иногда применяют неподвижный блок так, как показано на рис. 6, поднимая сами себя по веревке. Получается ли при этом выигрыш в силе по отношению к весу поднимаемого груза?
Плечами рычага в неподвижном блоке служат радиусы блока. Поскольку радиус постоянен, то выигрыша в силе неподвижный блок не даёт. Подъём в данном случае осуществляется за счёт мускульной силы человека, однако прилагаемое при этом усилие равно его весу. Ответ: выигрыша в силе в данном случае нет.
К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок без трения в оси, подвешены грузы с массами $m_1$ = 1 кг и $m_2$ = 2 кг. Каково ускорение, с которым движется второй груз?
Из условия невесомости и нерастяжимости нити следует, что сила натяжения нити на всех участках одинакова: $T_1 = T_2 = T$, и система тел движется как единое целое с одинаковым по модулю ускорением: $a_1 = a_2 = a$
Рассмотрим все силы действующие на каждый груз отдельно:
на I груз действуют: $m_1g$ и $T_1$; на II груз действуют: $m_2g$ и $T_2$
Систему отсчёта свяжем с Землёй.
$$m_1 = 1 кг$$ $$m_2 =2 кг$$ $$g = 9,81 м/c_2$$ $$а_2 — ?$$
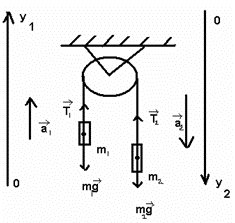
Проецируя вектора на координатные оси и учитывая равенство напряжений нити и ускорений, сложим почленно эти уравнения в скалярной форме:
+$ \begin
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 11 2021
Источник