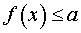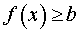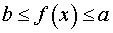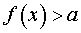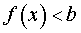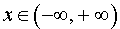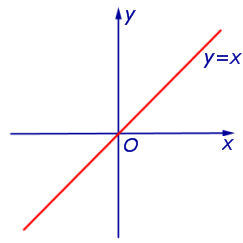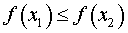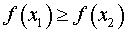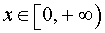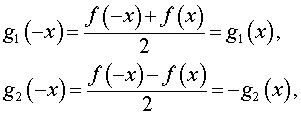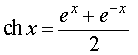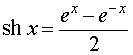Что значит неограниченная функция

Свойства функций. График функции

Содержание

Ограниченные и неограниченные функции

Монотонные и строго монотонные функции

Четные и нечетные функции

Периодические и непериодические функции. Период функции

График функции. Свойства графиков четных, нечетных, периодических функций

Ограниченные и неограниченные функции

Обозначим буквой X некоторое множество чисел, входящих в область определения D ( f ) функции y = f (x) .

ОПРЕДЕЛЕНИЕ 1. Функцию y = f (x) называют ограниченной сверху на множестве X , если существует такое число a , что для любого x из множества X выполнено неравенство

ОПРЕДЕЛЕНИЕ 2. Функцию y = f (x) называют ограниченной снизу на множестве X , если существует такое число b , что для любого x из множества X выполнено неравенство

ОПРЕДЕЛЕНИЕ 3. Функцию y = f (x) называют ограниченной на множестве X , если существуют такие числа a и b , что для любого x из множества X выполнено неравенство

ОПРЕДЕЛЕНИЕ 4. Функцию y = f (x) называют неограниченной сверху на множестве X , если для любого числа a существует такой x из множества X , для которого выполнено неравенство

ОПРЕДЕЛЕНИЕ 5. Функцию y = f (x) называют неограниченной снизу на множестве X , если для любого числа b существует такой x из множества X , для которого выполнено неравенство

ОПРЕДЕЛЕНИЕ 6. Функцию y = f (x) называют неограниченной на множестве X , если эта функция или неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.

Проиллюстрируем эти определения следующими примерами.

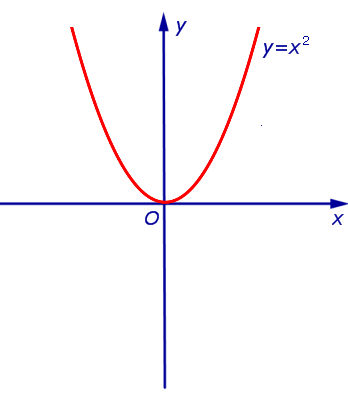
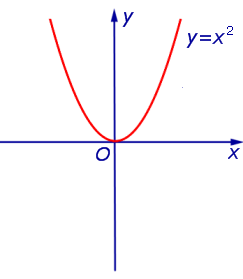
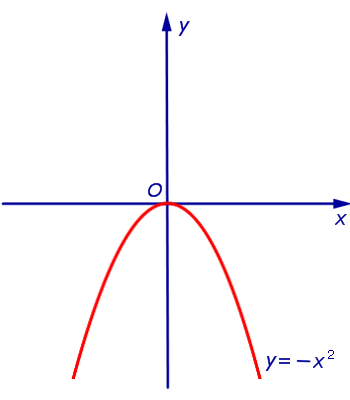
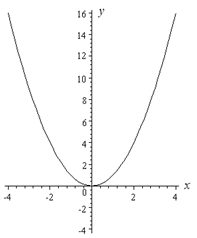
ПРИМЕР 1. Функция y = x 2 (рис. 1) является ограниченной снизу и неограниченной сверху на множестве

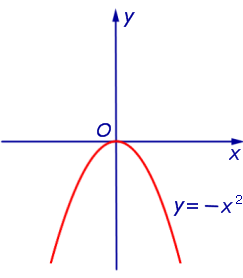
ПРИМЕР 2. Функция y = – x 2 (рис. 2) является ограниченной сверху и неограниченной снизу на множестве

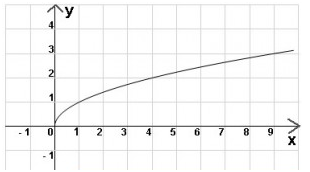
ПРИМЕР 3. Функция y = x (рис. 3) неограничена сверху и неограничена снизу на множестве

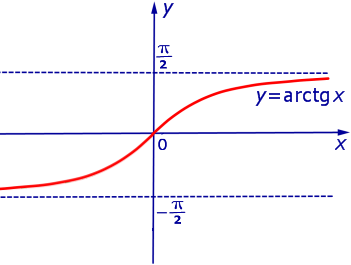
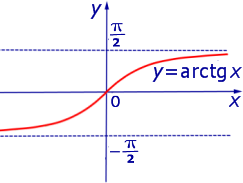
ПРИМЕР 4. Функция y = arctg x (рис. 4) ограничена на множестве

Монотонные и строго монотонные функции

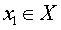
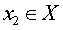
ОПРЕДЕЛЕНИЕ 7. Функцию y = f (x) называют возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

ЗАМЕЧАНИЕ 1. Возрастающие функции также называют неубывающими функциями.

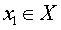
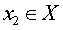
ОПРЕДЕЛЕНИЕ 8. Функцию y = f (x) называют убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

ЗАМЕЧАНИЕ 2. Убывающие функции также называют невозрастающими функциями.

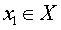
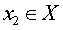
ОПРЕДЕЛЕНИЕ 9. Функцию y = f (x) называют строго возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

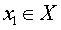
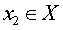
f (x₁) ОПРЕДЕЛЕНИЕ 10. Функцию y = f (x) называют строго убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x₁ выполнено неравенство

ОПРЕДЕЛЕНИЕ 11. Возрастающие и убывающие функции называют монотонными, строго возрастающие и строго убывающие функции называют строго монотонными.

ПРИМЕР 5. Функция y = x 2 (рис. 1) является строго убывающей функцией на множестве и строго возрастающей на множестве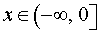

ПРИМЕР 6. Функция y = – x 2 (рис. 2) является строго возрастающей функцией на множестве и строго убывающей на множестве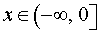

ПРИМЕР 7. Функция y = x (рис. 3) является строго возрастающей функцией на множестве

ПРИМЕР 8. Функция y = arctg x (рис. 4) является строго возрастающей на множестве

Четные и нечетные функции

ОПРЕДЕЛЕНИЕ 12. Функцию y = f (x) , определенную на множестве X , называют четной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство

ОПРЕДЕЛЕНИЕ 13. Функцию y = f (x) , определенную на множестве X , называют нечетной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство

ПРИМЕР 9. Функции y = x 2 и y = – x 2 являются четными функциями (рис. 1 и рис. 2), а функции y = x и y = arctg x являются нечетными функциями (рис. 3 и рис. 4).

ПРИМЕР 10. Примерами функций, которые не являются ни четными, ни нечетными функциями, являются показательные и логарифмические функции.

УТВЕРЖДЕНИЕ. Любую функцию y = f (x) , определенную на симметричном относительно точки x = 0 множестве X , можно представить в виде суммы четной и нечетной функций.

ДОКАЗАТЕЛЬСТВО. Рассмотрим две функции:

сумма которых равна f (x) , и заметим, что функция g₁ (x) является четной функцией, а функция g₂ (x) является нечетной функцией. Действительно,

что и завершает доказательство утверждения.

ЗАМЕЧАНИЕ 3. Раскладывая функцию y = e x в сумму четной и нечетной функций, получаем:

Функцию g₁ (x) называют гиперболическим косинусом и обозначают ch x :

Функцию g₂ (x) называют гиперболическим синусом и обозначают sh x :

Таким образом, справедливо равенство

Периодические и непериодические функции. Период функции

ОПРЕДЕЛЕНИЕ 14. Число называют периодом функции y = f (x) , если для любого числа числа x + T и x – T также принадлежат области определения D ( f ) и справедливы равенства

ОПРЕДЕЛЕНИЕ 15. Если функция имеет период, то ее называют периодической. Если же у функции периода нет, то ее называют непериодической.

ЗАМЕЧАНИЕ 4. Если число T является периодом некоторой функции, то и число kT , где k – любое целое число, отличное от нуля, также является периодом этой функции.

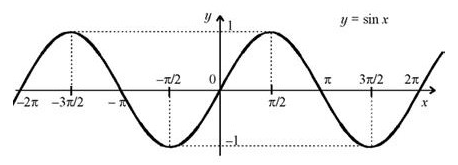
ПРИМЕР 11. Функции y = sin x и y = cos x являются периодическими функциями с периодом 2π , функции y = tg x и y = ctg x являются периодическими функциями с периодом π .

ПРИМЕР 12. Показательные, логарифмические и степенные функции являются непериодическими функциями.

График функции. Свойства графиков четных, нечетных, периодических функций

Рассмотрим плоскость с заданной прямоугольной системой координат Oxy .

ОПРЕДЕЛЕНИЕ 16. Графиком функции y = f (x) называют множество всех точек, координаты которых имеют вид (x; f (x)) , где .

ЗАМЕЧАНИЕ 6 . График периодической функции не изменяется при сдвиге вдоль оси абсцисс Ox на период вправо или влево (см., например, раздел «Графики тригонометрических функций» нашего справочника). Поэтому для того, чтобы построить график периодической функции с периодом T , достаточно построить график этой функции на любом отрезке оси абсцисс Ox длины T , а затем сдвигать его влево и вправо на расстояния nT , где n – любое натуральное число.

Источник

Что значит неограниченная функция

Функция y=f(x), определенная на множестве X, называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция f(x) ограничена сверху, если существует такая постоянная М, что для каждого \(x \in X\) выполняется неравенство \(f(x) \leqslant M.\)

· Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если множество её значений ограниченно снизу, то есть если существует такая постоянная М, что для каждого \(x \in X\) выполняется неравенство \(f(x) \leqslant M.\)

Например, таковыми являются показательные функции, функции \(y = >;y = \sqrt x .\)

График функции \(y = \) . Функция ограничена снизу значением y=0.

График функции \(y = \sqrt x \) . Функция ограничена снизу значением y=0.

· Функция f(x), определенная на множестве Х, называется ограниченной, если множество её значений ограниченно как сверху, так и снизу.

Примерами функций, ограниченных на всей числовой прямой, являются функции y=sin x, y=cos x.

График функции \(y = \sin x\) . Функция ограничена снизу значением y=-1 и сверху значением y=1.

При решении уравнений и неравенств свойство ограниченности функций часто играет определяющую роль. Например:

а) если для всех х из некоторого множества Х справедливы неравенства \(f(x) > M\) и \(g(x) , где М — некоторое число, то на множестве Х уравнение \(f(x) = g(x)\) и неравенство \(f(x) решений не имеют;

б) если для всех х из некоторого множества Х справедливы неравенства \(f(x) \geqslant M\) и \(g(x) \leqslant M\) , где М — некоторое число, то на множестве Х уравнение \(f(x) = g(x)\) равносильно системе:

Рассмотрим пример применения данных выводов.

Решение: Функции, записанные в левой и правой частях уравнения, определены при всех действительных значениях х. Кроме того, для любых х верно:

Следовательно, данное уравнение равносильно системе уравнений:

Решения второго уравнения системы есть х=0 и х=-1. Из этих значений первому уравнению удовлетворяет только х=0, которое, следовательно, является единственным решением исходного уравнения.

Источник