Что значит необратимая операция

необратимая операция

Тематики

Справочник технического переводчика. – Интент . 2009-2013 .

Смотреть что такое «необратимая операция» в других словарях:

необратимая операция (резервирования) — (МСЭ Т G.783). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN non revertive (protection) operation … Справочник технического переводчика

необратимая операция резервирования — (МСЭ Т G.798). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN non revertive protection operation … Справочник технического переводчика

Ампутация — Иллюстрация процесса ампутации из учебника хирургии (1537 год) Ампутация (лат. amputatio) усечение дистально расположенной части … Википедия

Травмати́ческий шок — синдром, возникающий при тяжелых травмах; характеризуется критическим снижением кровотока в тканях (гипоперфузией) и сопровождается клинически выраженными нарушениями кровообращения и дыхания. Патогенез. Ведущим патофизиологическим механизмом… … Медицинская энциклопедия

Кислород — (нем. Sauerstoff, франц. oxygène, англ. oxygen) нормальная и весьма важная составная часть воздуха, в обычных условиях температуры и давления бесцветный газ, без вкуса и запаха (история открытия К. см. Воздух). В виде соединений К. распространен… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Октябрьская революция — У этого термина существуют и другие значения, см. Октябрьская революция (значения). Октябрьское восстание … Википедия

Источник

Обратимые и необратимые операции

страница	22/32
Дата	14.02.2016
Размер	3,02 Mb.
Тип	Лекция

Обратимые и необратимые операции.

Не останавливаясь на истории вопроса, отметим, что принципиально этот вопрос был решен Я.Г. Синаем при рассмотрении системы «бильярд Синая».

Отражение шаров от выпуклой стенки. Числа Ляпунова положительны. Неустойчивость как основа необратимости. Необратимость же нужна для того, чтобы система забыла свое прошлое состояние.

Возникает естественный вопрос: нельзя ли преодолеть квазиклассический термодинамический барьер и сделать компьютер термодинамически и логически обратимым? Оказывается, в определенном смысле можно!

Если в системе произошло стирание или потеря одного бита информации, то статистический вес состояния соответствующего элемента увеличится вдвое, а его энтропия возрастает на . При этом неизменно происходит рассеяние энергии и выделение тепла (в этом состоит так называемый принцип Ландауэра), соответственно уменьшается свободная энергия элемента F. Таким образом, логически необратимая операция – стирание бита информации, является также и термодинамически необратимой операцией. Чтобы сделать необратимый компьютер хотя бы логически обратимым, необходимо сохранять всю информацию, которая терялась бы в других случаях в процессе его работы.

В качестве одной из возможностей существенного уменьшения рассеиваемой мощности широко обсуждается использование процессов переключения, настолько медленных по сравнению с процессами релаксации внутри логического элемента, что в каждый момент времени он оказывается в квазиравновесном состоянии. При таком квазистатическим или адиабатическом процессе энтропия логического элемента практически не изменяется и, следовательно, не происходит рассеяние энергии (), а минимальная работа переключения совпадает с изменением внутренней энергии и может быть в принципе возвращена для полезного использования. Описанные соображения лежат в основе так называемой адиабатической динамической логики. Кроме адиабатических процессов для уменьшения рассеиваемой мощности были предложены схемы, позволяющие исключить в процессе переключения логического элемента протекание в нем токов.

Логический элемент осуществляет логически обратимую операцию, когда сигнал на его входе может быть однозначно определен по сигналу на выходе. В последнее время был предложен целый ряд другого рода обратимых логических устройств. При этом было показано, что при наличии шумов полностью избежать диссипации энергии все-таки оказывается невозможно. Отметим, однако, что логическая обратимость не обязательно требует бездиссипативных энергетических процессов. В оптимальном классическом компьютере с соответствующей обратимой логической архитектурой промежуточные результаты не должны стираться, переходы между состояниями при промежуточных операциях не должны быть слишком быстрыми, а надежность результатов не должна быть чрезмерной, для того, чтобы процесс переключения мог считаться и термодинамически обратимым. Необратимыми в компьютере будут лишь периферийные процессы ввода и вывода информации.

Фредкин и Тоффоли обратили внимание на аналогию логических операций в компьютерах с элементарными физическими процессами. Существенным их достижением было изобретение умозрительной механической модели идеально упругих “бильярдных шаров”, где каждый шар представляет собой неразрушаемый бит. Модель позволяет получать наглядную картину обратимых операций в так называемом механическом баллистическом компьютере. Многоэтапные вычисления реализуются в нем как иерархия субвычислительных обратимых операций, которые осуществляются в процессе упругих столкновений движущегося шара-бита с совокупностью “управляющих” шаров и неподвижных отражателей, изменяющих определенным образом направление его движения. Запущенный в устройство с определенной скоростью шар-бит в результате выходит из него в состоянии с той же энергией, но с новым направлением скорости, а само устройство обратимым образом возвращается в исходное состояние. Энергетическая и энтропийная цена бита информации в этом случае определяется только количеством стираемой на выходе и генерируемой на входе компьютера информации, поскольку промежуточного стирания не происходит. Такого рода схема была названа консервативной логикой. Однако на самом деле из-за неидеальности шаров и отражателей их движение будет быстро хаотизироваться и вычислительный процесс разрушится. Для сохранения необходимого порядка в движении шаров предлагалось ввести дополнительный периодически движущийся потенциал.

Лекция 13

Концепции общей теории информации

Общее понятие Информации

Для того чтобы вывести наиболее общее определение понятия «Информация», выделим такое его свойство, которое с одной стороны было бы присущим любому его конкретному проявлению, и с другой стороны, позволяло бы отличать их от проявлений других понятий. Другими словами мы хотим выделить необходимый и достаточный признак, по которому мы будем определять, относится ли то или иное явление к проявлению понятия «Информации».

Начнем с того, что построим самую простую схему из трех понятий: «Объект», «Среда» и «Взаимодействие». «Объект» — это нечто устойчивое во времени и ограниченное в пространстве интересующее нас как единое целое. «Среда» — это множество всех других потенциальных «Объектов» интересующих нас только с точки зрения их влияния на состоянии выделенного «Объекта» и обратного влияния «Объекта» на их состояния. «Взаимодействие» — это растянутый во времени процесс взаимозависимого изменения параметров состояния «Объекта» и «Среды». Эта схема является замкнутой в том смысле, что «Среда» включает в себя все потенциальные «Объекты» способные влиять на состояние выделенного «Объекта». Далее мы не будем брать в кавычки приведенные понятия.

В природе существует два фундаментальных вида взаимодействия: обмен веществом и энергией. Фундаментальность этих видов взаимодействия заключается в том, что все прочие взаимодействия происходят только через их посредство. Эти виды взаимодействия подчиняются закону сохранения. Сколько вещества и энергии один объект передал другому, столько тот и получил, и наоборот. Потери, происходящие при передаче, не рассматриваются, ибо потери вещества и энергии в замкнутой среде не возможны и то, что называют потерями, является отдельными актами взаимодействия с другими объектами той же среды. Среда замкнута именно в том смысле, что все взаимодействия происходят только внутри ее.

Энергетическое и вещественное взаимодействие объектов является симметричным, т.е. сколько один отдал столько же другой получил. Переходы между веществом и энергией не влияют на общий баланс, поскольку действуют законы сохранения константы их соотношения. Так же не влияет на общий баланс разрушение объекта в результате таких взаимодействий, так как опять же сохраняется сумма констант соотношения вещества и энергии, образовавшихся в результате разрушения частей (новых объектов).

Примем за аксиому, что на основе комбинации фундаментальных взаимодействий, между объектами может происходить взаимодействие более высокого порядка, при котором от одного к другому переходит некоторая субстанция и при этом потери одного не совпадают с приобретением другого. Такое взаимодействие является несимметричным. В предельном случае несимметричного взаимодействия при передаче субстанции между объектами один из них ее приобретает, а другой не теряет. Изменение количества энергии и вещества при этом естественно, будут иметь место, поскольку данный акт взаимодействия имеет в своей основе комбинацию фундаментальных видов взаимодействия обеспечивающих перенос субстанции.

Теперь сформулируем наиболее общее определение понятия Информации, от которого мы будем отталкиваться в дальнейшем.

Любое взаимодействие между объектами, в процессе которого один приобретает некоторую субстанцию, а другой ее не теряет называется информационным взаимодействием. При этом передаваемая субстанция называется Информацией.

Из этого определения следует два наиболее общих свойства Информации. Первое — Информация не может существовать вне взаимодействия объектов. Второе — Информация не теряется ни одним из них в процессе этого взаимодействия.

Источник

необратимая операция

Большой англо-русский и русско-английский словарь . 2001 .

Смотреть что такое «необратимая операция» в других словарях:

необратимая операция — (МСЭ Т G.798). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN non revertive operation … Справочник технического переводчика

необратимая операция (резервирования) — (МСЭ Т G.783). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN non revertive (protection) operation … Справочник технического переводчика

необратимая операция резервирования — (МСЭ Т G.798). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN non revertive protection operation … Справочник технического переводчика

Ампутация — Иллюстрация процесса ампутации из учебника хирургии (1537 год) Ампутация (лат. amputatio) усечение дистально расположенной части … Википедия

Травмати́ческий шок — синдром, возникающий при тяжелых травмах; характеризуется критическим снижением кровотока в тканях (гипоперфузией) и сопровождается клинически выраженными нарушениями кровообращения и дыхания. Патогенез. Ведущим патофизиологическим механизмом… … Медицинская энциклопедия

Кислород — (нем. Sauerstoff, франц. oxygène, англ. oxygen) нормальная и весьма важная составная часть воздуха, в обычных условиях температуры и давления бесцветный газ, без вкуса и запаха (история открытия К. см. Воздух). В виде соединений К. распространен… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Октябрьская революция — У этого термина существуют и другие значения, см. Октябрьская революция (значения). Октябрьское восстание … Википедия

Источник

«Иная» логика и обратимые вычисления

В конце прошлого года Google Translate к выходу нового эпизода «Звёздных войн» добавил поддержку «Галактического языка» Ауребеш. Правда оказалось, что при выборе этого языка просто происходит перевод на английский. Если использовать Chrome или Firefox, то появляется шрифт, в котором вместо латиницы подставлены символы ауребеш, ну а в IE без особых хитростей выводится английский текст.

Начал вспоминать другие примеры создания «языков чужаков». Например, язык Клингонов из «Звёздного пути» тоже основан на латинице, но при этом достаточно проработан, имеет свой синтаксис и словарь. Языки народов Средиземья из «Властелина колец» – вообще отдельная история.

А ещё существуют такие языки, как Линкос, специально разработанный Гансом Фройденталем для межпланетного общения и основанный на предположении, что математика является универсальным языком общения для любых разумных существ.

В «Плоском мире» Терри Пратчетта тоже достаточно языков, но вроде это просто переименованные земные языки. А в отношении математики, как универсального языка, более уместно упомянуть английского биолога Джека Коэна, его соавтора по книге «Наука плоского мира», который на одной конференции затронул достаточно неожиданную тему: «Почему вы думаете, что пришельцы поймут вашу математику? А вдруг у них совершенно другой способ мышления?»

Эту цитату я прочитал у Джеймса Нэйшина, другого участника конференции, профессора университета на Гавайях, где она и проходила. На его сайте можно найти тексты двух выступлений, в какой-то мере спровоцированных данным вопросом: «Как пришельцы делают математику» и «Логика иных планет». Может это и выглядит не очень серьёзно, особенно когда разные виды логики приписаны жителями разных планет нашей солнечной системы. Однако, вот искал возможные ссылки на одну функцию, используемую для создания обратимых вентилей, и с удивлением обнаружил её у него в разделе, посвящённом логике жителей Юпитера.

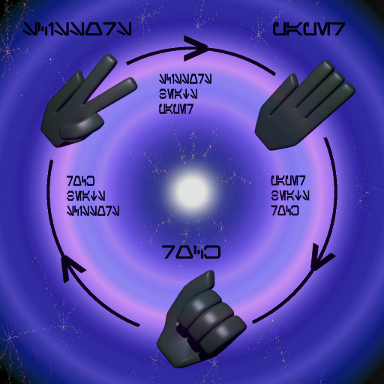
Камень, ножницы, бумага

Что же особенного в «юпитерианской логике» и как она связана с обратимыми вычислениями? Нэйшин для её описания использует набор из трёх элементов, обозначаемых символами R,P,S, которые соответствуют первым буквам английских слов для камня, ножниц и бумаги. Игра «камень, ножницы, бумага» (о ней тут тоже писали и не раз) известна и на Гавайях как «дзян-кэн». По правилам игры один из трёх предметов побеждает другой исходя из циклического набора предпочтений. Это обычно изображается на круговой диаграмме, но можно записать и в строчку:

S обычной логики. Так что, задание отношений между элементами определяет аналоги логических операций. Правда, при циклическом наборе предпочтений между трёмя элементами некоторыми свойствами приходится пожертвовать. Что поделать, иная логика.

Таблица для аналога «ИЛИ» при таком подходе выглядит как

Иное ИЛИ	R	P	S
R	R	P	R
P	P	P	S
S	R	S	S

Таблица для операции «И» стоится аналогично

Иное И	R	P	S
R	R	R	S
P	R	P	P
S	S	P	S

Обратимые вычисления

А что с обратимыми вычислениями? О них уже тут тоже писали как, впрочем, и о троичной логике (тут, на geektimes, ещё тут) и даже вместе их пытались свести.

Обратимые вентили могут быть полезными для решения проблемы тепловыделения в процессорах следующих поколений, они тесно связаны с теорией квантовых вычислений. Да и тема сама по себе достаточно интересная. Об этом можно много где почитать, включая приведённые выше ссылки, так что постараюсь не особо распространяться на тему уже достаточно известных вещей.

Если совсем коротко, то вентиль обратим, когда значения на входах всегда можно восстановить по значениям на выходах. Для работы с двоичными данными обычно используют универсальные вентили Тоффоли или Фредкина. Оба вентиля имеют по три входа и три выхода, так как, в отличие от необратимого случая, из обратимых двоичных вентилей с двумя входами нельзя создать набор для выполнения произвольной операции над данными.

Попробуем представить обратимый аналог обычного вентиля «ИЛИ». Предположим, что у него два входа (и два выхода, раз уж он должен быть обратимым), на входы подаются двоичные значения, а один из выходов должен выдать результат операции «ИЛИ». Получается, что одно и то же значение 1 (ИСТИНА) на этом выходе может получиться при трёх разных комбинациях на входе: 11, 01, 10. Если бы второй выход мог иметь три разных значения, это можно было бы использовать для обращения такого вентиля.

Так что, уже достаточно простые оценки приводят к идее использовать троичную систему хотя бы на одном выходе. А что если попробовать работать с тремя значения на всех входах и выходах – можно ли получить обратимый вентиль, если использовать троичную логику?

Достаточно распространённой является троичная логика Лукасевича. Она может быть построена и уже упомянутым выше трюком с максимум и минимумом, если предположить, что третьему значению соответствует какое-нибудь число x, 0 00 01 0x 10 11 1x x0 x1 xx

и так как вентиль обратим, то и на выходе каждая из этих девяти пар должна появиться при одной из комбинаций на входе. Видно, что в этих парах любое значение первого (и второго) элемента встретится по три раза.

То есть, три нуля, три единицы, три икса. А вместо этого в таблице для троичного «ИЛИ» стоит только один ноль и пять единиц. Во второй таблице для «И» наоборот, пять нулей и одна единица, что тоже не подходит.

Поэтому, хотя обратимые троичные вентили по отдельности и троичная логика по отдельности достаточно широко используются, вместе их трудно свести. Тут и приходит на помощь «инопланетная» логика. Для наглядности заменим R,P,S на 0,1,$.

Вот таблица для «ИЛИ»

«Иное ИЛИ»	0	1	$
0	0	1	0
1	1	1	$
$	0	$	$

Для значений 0, 1 оно совпадает с обычным «ИЛИ», но при этом обладает уже упомянутым свойством, необходимым для создания обратимого троичного вентиля (каждое значение встречается по три раза). Ситуация с таблицей для операции «И» аналогична

«Иное И»	0	1	$
0	0	0	$
1	0	1	1
$	$	1	$

Теперь, чтобы построить полный вариант обратимых троичных вентилей надо ещё подобрать таблицу для второго, вспомогательного выхода. В обычной арифметике для обращения функции max(a,b) на втором выходе можно было бы использовать b–a. Нечто похожее можно использовать и в нашем примере

«Иная разность»	0	1	$
0	0	$	1
1	1	0	$
$	$	1	0

Подошло – вот так будет выглядеть полный троичный обратимый вентиль «ИЛИ»

Вход	00	01	0$	10	11	1$	$0	$1	$$
Выход	00	11	0$	1$	10	$1	01	$$	$0

Видно, что каждая из девяти возможных комбинаций встречается на выходе по одному разу, так что операция обратима. Действие этого вентиля можно ещё описать следующим образом: он не изменяет пары 00, 0$, переставляя по циклу семь пар (01, 11, 10, 1$, $1, $$, $0)

Так что, семикратное применение вентиля оставит любую пару значений без изменений, а обратная операция соответствует применению шести вентилей подряд. С вентилями Тоффоли и Фредкина проще, каждый из них совпадает со своим обратным.

Если подавать на вход только значения ноль и единица, то этот троичный вентиль реализует обычную логическую операцию «ИЛИ». Установив единицу на второй вход можно использовать второй выход как операцию «НЕ» от первого входа. Помимо этого, вентиль реализует операцию «разветвления» двоичного значения поданного на второй вход, если на первый подать ноль. Так что этот обратимый троичный вентиль является универсальным для работы с двоичными данными.

Пример обратимого троичного вентиля «И» аналогичен

Вход	00	01	0$	10	11	1$	$0	$1	$$
Выход	00	01	$$	0$	10	11	$1	1$	$0

Этот вентиль не изменяет пары 00 и 01, переставляя по циклу пары
(0$, $$, $0, $1, 1$, 11, 10, 0$)

Он тоже универсален для двоичных операций, но в отличие от «ИЛИ», одного такого вентиля не достаточно для «разветвления». Правда, выбор операции на втором выходе был достаточно произволен. Операция же на первом входе однозначно определяются выбором трёх условий: (1) выполнять нужную логическую операцию для двоичных данных, (2) соответсвовать одному из значений на входе, (3) не зависеть от их перестановки.

Выбор второй операции тоже достаточно естественен и может быть использован для других моделей. Предположим, надо построить обратимый вентиль для логики Лукасевича. Проблема с этим уже была описана, некоторые значения появляются в таблице 3×3 пять раз, а их должно быть поровну, чтобы сделать обратимый вентиль.

Ещё ящерица и Спок

Тут можно применить ту же идею, что и при расширении двоичной логики до системы из трёх элементов и исходя из имеющейся проблемы с пятью повторениями в таблице для троичной логики Лукасевича (0, 1, x), нужно добавить ещё два элемента ($ и @). Другой аргумент в пользу пяти значений связан с использованием аналога разности b-a для обращения максимума и минимума: разница между тремя целыми значениями от 0 до 2 может принимать пять разных значений от -2 до 2.

Соотношения между элементами можно опять изобразить на круговой диаграмме или записать в строчку
0
Соответствующая игра тоже известна. Например, её версия была показана в сериале «Теория Большого взрыва» (картинка с объяснением). Соответствия можно выбрать такие: 0 -камень, 1 – бумага, $ — ножницы, @ — ящерица, x — Спок (уроженец планеты Вулкан в сериале «Звёздый путь»).

Можно продолжать и дальше; для построения похожих круговых диаграмм, особенно хорошо подходят наборы, в которых количество элементов равно простому числу.

Коллективная логика и «невозможные стрелки»

Надо сказать, что циклическая логика не такая уж «инопланетная». Один из наиболее характерных примеров связан с парадоксами Кондорсе и Эрроу относящимися к проблеме выбора. Типичное описание «парадокса голосования» можно найти в книге лауреата Нобелевской премии по экономике Кеннета Эрроу «Коллективный выбор и индивидуальные ценности».

Рассмотрим выбор из трёх альтернатив (например, выборы с тремя кандидатами) A, B, C. При этом, каждый голосующий имеет некую упорядоченную систему предпочтений. То есть, если первая альтернатива предпочтительнее второй, а вторая предпочтительная третьей, то первая тоже предпочтительнее третьей. Пример проблем с выбором, возникающий при нарушении этого критерия, тоже описан далее.

Такие упорядоченные предпочтения являются примером транзитивных отношений, а операции с аналогичным свойством ассоциативны, то есть, не зависят от расстановки скобок. Обсуждаемое ранее определение операции «ИЛИ» через задание отношений элементов хорошо согласуется с идеей выбора: операция «А ИЛИ В» – просто выбор между A и B, исходя из некого набора предпочтений (включая случай «А ИЛИ A», который, хотя и затруднительно назвать «выбором», тоже имеет вполне определённый результат, A).

Пусть кто-то полагает, что B лучше A, C лучше В (и по приведённому ранее критерию, C лучше A). Запишем этот выбор как
(1) A ((A || B) || C) = B || C = C,
(A || (B || C)) = A || C = A

Источник