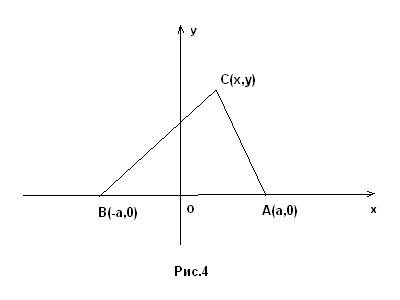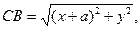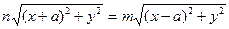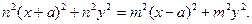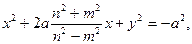Что значит найти геометрическое место точек

Геометрическое место точек

Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.

Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:

1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;

2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.

(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).

Геометрическое место точек, равноудалённых от данной точки — окружность.

Это следует непосредственно из определения окружности.

Некоторые теоремы о ГМТ

1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.

2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.

3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.

4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.

Понятие ГМТ часто используют при решении задач на построение.

Источник

Геометрические места точек

Определение.

Геометрическим местом точек (в дальнейшем ГМТ), называется фигура плоскости, состоящая из точек обладающих некоторым свойством, и не содержащая ни одной точки, не обладающей этим свойством.

Мы будем рассматривать только те ГМТ, которые можно построить с помощью циркуля и линейки.

Рассмотрим ГМТ на плоскости, обладающие простейшими и наиболее часто выражающимися свойствами:

1) ГМТ, отстоящих на данном расстоянии r от данной точки О, есть окружность с центром в точке О радиуса r.

2) ГМТ равноудаленных от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ и проходящая через его середину.

3) ГМТ равноудаленных от двух данных пересекающихся прямых, есть пара взаимно перпендикулярных прямых, проходящих через точку пересечения и делящих углы между данными прямыми пополам.

4) ГМТ, отстоящих на одинаковом расстоянии h от прямой, есть две прямые, параллельные этой прямой и находящиеся по разные стороны от нее на данном расстоянии h.

5) Геометрическое место центров окружностей, касающихся данной прямой m в данной на ней точке М, есть перпендикуляр к АВ в точке М (кроме точки М).

6) Геометрическое место центров окружностей, касающихся данной окружности в данной на ней очке М, есть прямая, проходящая через точку М и центр данной окружности (кроме точек М и О).

7) ГМТ, из которых данный отрезок виден под данным углом, составляет две дуги окружностей, описанных на данном отрезке и вмещающих данный угол.

8) ГМТ, расстояния от которых до двух данных точек А и В находятся в отношении m : n, есть окружность (называемая окружностью Аполлония).

9) Геометрическое место середин хорд, проведенных из одной точки окружности, есть окружность, построенная на отрезке, соединяющем данную точку с центром данной окружности, как на диаметре.

10) Геометрическое место вершин треугольников равновеликих данному и имеющих общее основание, составляет две прямые, параллельные основанию и проходящие через вершину данного треугольника и ему симметричного относительно прямой, содержащей основание.

Приведем примеры отыскания ГМТ.

ПРИМЕР 2. Найти ГМТ, являющихся серединами хорд, проведенных из одной точки данной окружности (ГМТ № 9).

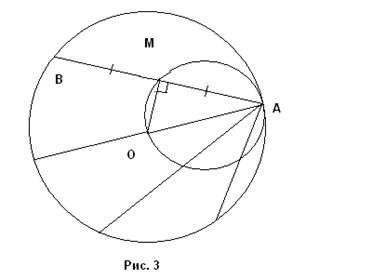
Решение . Пусть дана окружность с центром О и на этой окружности выбрана точка А из которой проводятся хорды. Покажем, что искомое ГМТ есть окружность, построенная на АО как на диаметре (кроме точки А) (рис. 3).

Пусть АВ — некоторая хорда и М – ее середина. Соединим М и О. Тогда МО ^ АВ (радиус, делящий хорду пополам, перпендикулярен этой хорде). Но, тогда ÐАМО = 90 0 . Значит М принадлежит окружности с диаметром АО (ГМТ № 7). Т.к. эта окружность проходит через точку О, то О принадлежит нашему ГМТ.

Обратно, пусть М принадлежит нашему ГМТ. Тогда, проведя через М хорду АВ и соединив М и О, получим, что ÐАМО = 90 0 , т.е. МО ^ АВ, а, значит, М – середина хорды АВ. Если же М совпадает с О, то О — середина АС.

Часто метод координат позволяет находить ГМТ.

ПРИМЕР 3. Найти ГМТ, расстояние от которых до двух данных точек А и В находятся в данном отношении m : n (m ≠ n).

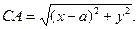
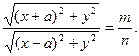
Решение . Выберем прямоугольную систему координат так, чтобы точки А и В располагались на оси Ох симметрично относительно начала координат, а ось Оу проходила через середину АВ (рис.4). Положим АВ = 2a. Тогда точка А имеет координаты А (a, 0), точка В — координаты В (-a, 0). Пусть С принадлежит нашему ГМТ, координаты С(х, у) и CB/CA = m/n. Но Значит

(*)

Преобразуем наше равенство. Имеем

После раскрытия скобок и приведения подобных слагаемых, получаем

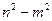
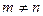
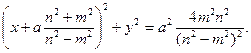
Разделим левую и правую части последнего неравенства на (это можно сделать, так как по условию ), затем выделим полный квадрат относительно х. Получаем

или

(**)

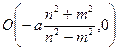
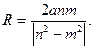
Но последнее уравнение задает окружность с центром в точке и радиусом Таким образом, если точка удовлетворяет условиям задачи, то она принадлежит (**).

Обратно, пусть координаты точки С(x,y) удовлетворяют уравнению (**). Проделывая все выкладки в обратную сторону, приходим к равенству (*), что и доказывает принадлежность точки С нашему ГМТ.

Источник

Геометрические места точек

Описание презентации по отдельным слайдам:

Описание слайда:

Геометрические места точек
Геометрическим местом точек (ГМТ) называется фигура, состоящая из всех точек, удовлетворяющих заданному свойству или нескольким заданным свойствам.
Примерами геометрических мест точек являются:
окружность – ГМТ, удаленных от данной точки на данное расстояние;
круг – ГМТ, удаленных от данной точки на расстояние, не превосходящее данное.

Описание слайда:

Упражнение 1
Отметьте точки, расположенные в узлах сетки и удаленные от точки O на расстояние, равное 2. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 2
Отметьте точки, расположенные в узлах сетки и удаленные от точки O на расстояние, меньшее 2. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 3
Отметьте точки, расположенные в узлах сетки и удаленные от точки O на расстояние, большее 2 и меньшее 3. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 4
Отметьте точки, расположенные в узлах сетки, расстояния от которых до точек A и B меньше трех. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 5
Отметьте точки, расположенные в узлах сетки, расстояния от которых до точек A и B меньше или равны двум. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 6
Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A меньше трех, а расстояние до точки B меньше двух. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 7
Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A больше двух, а расстояние до точки B меньше двух. (Стороны клеток равны 1).
Ответ:

Описание слайда:

Упражнение 8
Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A меньше, чем расстояние до точки B, и расстояние до точки B меньше, чем расстояние до точки C.
Ответ:

Описание слайда:

Упражнение 9
Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A больше, чем расстояние до точки B, и расстояние до точки B меньше, чем расстояние до точки C.
Ответ:

Описание слайда:

Упражнение 10
Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 90о.
Ответ:

Описание слайда:

Упражнение 11
Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 90о.
Ответ:

Описание слайда:

Упражнение 12
Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 90о.
Ответ:

Описание слайда:

Упражнение 13
Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 45о.
Ответ:

Описание слайда:

Упражнение 14
Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 45о.
Ответ:

Описание слайда:

Упражнение 15
Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 135о.
Ответ:

Описание слайда:

Серединный перпендикуляр
Теорема. Серединный перпендикуляр к отрезку является ГМТ, одинаково удаленных от концов этого отрезка.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Доказательство. Пусть дан отрезок АВ и точка О – его середина. Очевидно, точка О одинаково удалена от точек А, В и принадлежит серединному перпендикуляру.
Обратно, пусть точка С принадлежит серединному перпендикуляру и не совпадает с О, тогда прямоугольные треугольники АОС и ВОС равны (по катетам). Следовательно, АС=ВС.
Пусть точка С одинаково удалена от точек А и В и не совпадает с точкой О. Тогда треугольник АВС равнобедренный и СО – медиана. По свойству равнобедренного треугольника медиана является также и высотой. Значит, точка С принадлежит серединному перпендикуляру.

Описание слайда:

Упражнение 1
Изобразите ГМТ, равноудаленных от точек A и B.
Ответ:

Описание слайда:

Упражнение 2
На прямой c изобразите точку C, равноудаленную от точек A и B.
Ответ:

Описание слайда:

Упражнение 3
Изобразите ГМТ, равноудаленных от точек A и B.
Ответ:

Описание слайда:

Упражнение 4
На прямой c изобразите точку C, равноудаленную от точек A и B.
Ответ:

Описание слайда:

Упражнение 5
Изобразите ГМТ, равноудаленных от точек A и B.
Ответ:

Описание слайда:

Упражнение 6
На прямой c изобразите точку C, равноудаленную от точек A и B.
Ответ:

Описание слайда:

Упражнение 7
Отметьте точку, равноудаленную от точек A, B и C.
Ответ:

Описание слайда:

Упражнение 8
Отметьте точку, равноудаленную от точек A, B и C.
Ответ:

Описание слайда:

Упражнение 9
Отметьте точку, равноудаленную от точек A, B и C.
Ответ:

Описание слайда:

Упражнение 10
Изобразите геометрическое место центров окружностей, проходящих через две данные точки.
Ответ: Серединный перпендикуляр к отрезку, соединяющему две данные точки.

Описание слайда:

Упражнение 11
Изобразите геометрическое место вершин С равнобедренных треугольников с заданным основанием AB.
Ответ: Серединный перпендикуляр к отрезку AB без середины этого отрезка.

Описание слайда:

Упражнение 12
Пусть А и В — точки плоскости. Укажите геометрическое место точек С, для которых АС ВС.
Ответ: Полуплоскость, определяемая серединным перпендикуляром к отрезку AB, содержащая точку A.

Описание слайда:

Упражнение 13
Пусть А и В точки плоскости, c — прямая. Укажите геометрическое место точек прямой c, расположенных ближе к А, чем к В. В каком случае таких точек нет?
Ответ: Часть прямой c, лежащая внутри полуплоскости, определяемой серединным перпендикуляром к отрезку AB и точкой A. Если прямая c целиком лежит в полуплоскости, определяемой серединным перпендикуляром и точкой B, то таких точек нет.

Описание слайда:

Биссектриса угла
Теорема. Биссектриса угла является ГМТ, лежащих внутри этого угла и одинаково удаленных от его сторон.
Если CA = CB, то прямоугольные треугольники АOС и ВOС равны (по гипотенузе и катету). Следовательно, углы AOC и BOC равны. Значит, точка C принадлежит биссектрисе угла. Обратно, если точка C принадлежит биссектрисе угла, то прямоугольные треугольники AOC и BOC равны (по гипотенузе и острому углу). Следовательно, AC = BC. Значит, точка С одинаково удалена от сторон данного угла.
Доказательство. Рассмотрим угол c вершиной в точке О и сторонами а, b. Пусть точка С лежит внутри данного угла. Опустим из нее перпендикуляры СА и CB на стороны а и b.

Описание слайда:

Упражнение 1
Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
Ответ:

Описание слайда:

Упражнение 2
На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
Ответ:

Описание слайда:

Упражнение 3
Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
Ответ:

Описание слайда:

Упражнение 4
На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
Ответ:

Описание слайда:

Упражнение 5
Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
Ответ:

Описание слайда:

Упражнение 6
На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
Ответ:

Описание слайда:

Упражнение 7
Что является геометрическим местом центров окружностей касающихся двух данных пересекающихся прямых?
Ответ: Биссектрисы углов, образующихся при пересечении данных прямых, без точки пересечения этих прямых.

Описание слайда:

Упражнение 8
Ответ: а) Точки, принадлежащие биссектрисам четырех углов, образованных данными прямыми;
б) внутренности двух вертикальных углов, образованных биссектрисами.
Пусть a и b — пересекающиеся прямые. Найдите геометрическое место точек: а) одинаково удаленных от a и b; б) расположенных ближе к a, чем к b.

Описание слайда:

Упражнение 9
На прямой c, пересекающей стороны угла, найдите точку C, одинаково удаленную от этих сторон.
Ответ: Точка пересечения данной прямой с биссектрисой данного угла.

Описание слайда:

Упражнение 10
Дан угол АOB и точки M, N на его сторонах. Внутри угла найдите точку, одинаково удаленную от точек M и N и находящуюся на одинаковом расстоянии от сторон угла.
Ответ: Точка пересечения серединного перпендикуляра к MN с биссектрисой угла.

Описание слайда:

Пересечение фигур
Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура Ф, состоящая из всех точек, принадлежащих фигуре Ф1 и фигуре Ф2, называется пересечением фигур Ф1 и Ф2 и обозначается Ф1 Ф2.

Описание слайда:

Упражнение 1
Ответ: Искомое ГМТ является пересечением двух кругов с центрами в точках O1, O2 и радиусами R1, R2.
Даны две точки O1 и O2. Найдите ГМТ X, для которых XO1 R1 и XO2 R2. Пересечением каких фигур является искомое ГМТ.

Описание слайда:

Упражнение 2
Даны две точки A и B. Найдите ГМТ C, для которых CA CB AB. Пересечением каких фигур является искомое ГМТ.
Ответ: Искомое ГМТ является пересечением круга и полуплоскости.

Описание слайда:

Упражнение 3
Даны три точки A, B, C. Найдите ГМТ X, для которых AX BX и BX CX. Пересечением каких фигур является искомое ГМТ.
Ответ: Искомое ГМТ является пересечением двух полупространств, определяемых серединными перпендикулярами к отрезкам AB и BC.

Описание слайда:

Объединение фигур
Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура Ф, состоящая из всех точек, принадлежащих фигуре Ф1 или фигуре Ф2, называется объединением фигур Ф1 и Ф2 и обозначается Ф1 Ф2.

Описание слайда:

Упражнение 1
Даны две точки O1 и O2. Найдите ГМТ X, для которых XO1 R1 или XO2 R2. Объединением каких фигур является искомое ГМТ.
Ответ: Искомое ГМТ является объединением двух кругов с центрами в точках O1, O2 и радиусами R1, R2.

Описание слайда:

Упражнение 2
Даны три точки A, B, C. Найдите ГМТ X, для которых AX BX или BX CX. Объединением каких фигур является искомое ГМТ.
Ответ: Искомое ГМТ является объединением двух полупространств, определяемых серединными перпендикулярами к отрезкам AB и BC.

Описание слайда:

Разность фигур
Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура Ф, состоящая из всех точек, принадлежащих фигуре Ф1 и не принадлежащих фигуре Ф2, называется разностью фигур Ф1 и Ф2 и обозначается Ф1 \ Ф2.

Описание слайда:

Упражнение 1
Ответ: Искомое ГМТ является разностью двух кругов с центрами в точках O1, O2 и радиусами R1, R2.
Даны две точки O1 и O2. Найдите ГМТ X, для которых XO1 R1 и XO2 R2. Разностью каких фигур является искомое ГМТ.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Охрана труда

• Сейчас обучается 101 человек из 49 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 351 человек из 64 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 201 человек из 54 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Популярно о криптографии Основные понятия

Образец выполнения домашнего задания

ГОРОД-ГЕРОЙ ВОЛГОГРАД

Календарный год состоит из четырех сезонов, иначе их еще называют «времена года» — из зимы, весны, лета и осени. Давай поговорим поп

Кредитные продукты

Оптическое просветление биологических тканей – перспективы применения в медицинской диагностике и фототерапии

Внешнеэкономическая деятельность российских предприятий Начальник управления инновационной деятельности ЮФУ – Кучинский Ле

Инсталляция и конфигурирование программы в локальной сети

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5412365 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Москве новогодние каникулы в школах могут начаться с 27 декабря

Время чтения: 1 минута

НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В российских школах могут появиться «службы примирения»

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

При детском омбудсмене в России создадут платформу для взаимодействия с родителями

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник