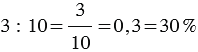Что значит найдите отношение длин

Длина отрезка

Отрезок — это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.

Измерить отрезок — значит найти его длину (расстояние между его концами).

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

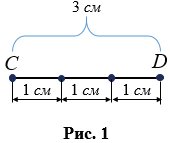
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

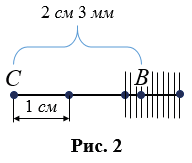
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

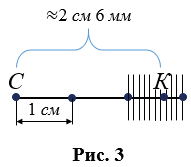
• Если точность измерения не имеет большой роли, то, как видно на Рис.3, в отрезке СК сантиметр укладывается два раза с остатком, в остатке миллиметр укладывается 6 раз с остатком, говорят о приближенных значениях, т.е. длина отрезка приближенно равна 2,6 смили 2 см 6 мм, и записывают длина отрезка СК2,6 см(СК2 см 6 мм).

• Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Длина отрезка — это всегда какое-то положительное число.

Свойства длин отрезков:

1. Равные отрезки имеют равные длины.
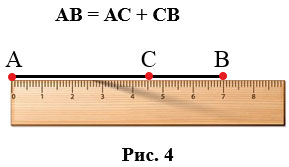
2. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.

1. Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записываютMN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.

Поделись с друзьями в социальных сетях:

Источник

Отношения

Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.

Частное двух чисел и , отличных от нуля, называют отношением чисел и , или отношением числа к числу .

Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.

14 : 7 — отношение числа 14 к числу 7;

6 : 25 — отношение числа 6 к числу 25;

— отношение числа к числу ;

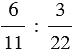
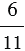
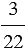
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.

Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .

Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .

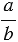
Основное свойство отношения:

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Запишем отношение числа 3 к числу 10 и найдем его значение:

То есть отношение двух чисел можно выразить в процентах.

Процентное отношение двух чисел — это их отношение, выраженное в процентах.

Процентное отношение показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Пример:

Сколько процентов составляет число 5 от числа 10?

5 10 2 1 · 100 % = 1 2 · 100 % = 100 2 % = 50 % .

Ответ: 50% составляет число 5 от числа 10.

Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.

Например:

Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.

Отношение длины прямоугольника к его ширине равно 12 : 100 = .

Отношение ширины прямоугольника к его длине равно 100 : 12 = .

Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).

Пусть на карте задан масштаб 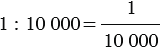, то есть карта сделана в масштабе одна десятитысячная.

Найдем, какой длине на местности соответствует отрезок 5 см на карте.

Для решения обозначим через длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:

5 : = 1 : 10 000;

Решаем данное уравнение:

= 510 000;

= 50 000;

50 000 см = 500 м = 0,5 км.

Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.

Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.

Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

: 9,5 = 1 : 10 000;

Решаем данное уравнение:

= 9,5 : 10 000;

= 0,00095;

0,00095 км = 0,95 м = 95 см.

Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.

Поделись с друзьями в социальных сетях:

Источник

Математика. 6 класс

Конспект урока

Отношение чисел и величин

Перечень рассматриваемых вопросов:

• Понятия отношения чисел и величин.
• Свойства отношений.
• Понятия отношений величин одного наименования и разных.

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Отношение величин одного наименования (длин, скоростей, стоимостей и т. д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.

Отношение величин различных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма и т. д.) есть новая величина.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Цена товара – это отношение стоимости товара к количеству единиц товара.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Отношения чисел и величин мы с вами встречаем не только в математике, но в географии. Давайте же разберёмся с этим понятием и научимся его использовать.

Частное двух не равных нулю чисел a и b называют отношением числа a к числу b.

Числа a и b называют членами отношения.

Отношение – a к b

Отношение величин одного наименования (длины, скорости, стоимости и т. д., выраженных одинаковыми единицами измерения) есть число.

Мешок с красными яблоками весит 20 кг, а мешок с зелёными весит 10 кг. Во сколько раз мешок с красными яблоками тяжелее мешка с зелёными? Какую часть от красных яблок составляют зелёные?

Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма) есть новая величина.

Цена товара – это отношение стоимости товара к его количеству единиц товара.

За 4 шоколадки заплатили 48 рублей. Сколько стоит одна шоколадка?

Так как цена всей покупки составила 48 рублей, а купили мы 4 шоколадки, для нахождения цены одной шоколадки, нужно всю цену разделить на количество шоколадок.

Разбор заданий тренировочного модуля

№ 1. Ввод с клавиатуры пропущенных элементов в тексте.

Впишите ответ. Садовый участок имеет прямоугольную форму, его площадь равна 1000 кв. м. Длина участка равна 100 м. Найдите отношение длины участка к его ширине.

№ 2. Единичный / множественный выбор.

Источник