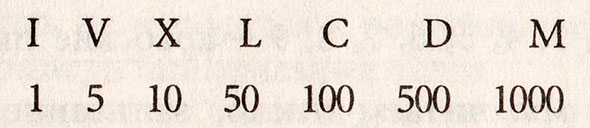Что значит натуральное число пример

Натуральные числа: что такое натуральное число в математике

Содержание:

В математике существует несколько видов чисел. Одними из самых известных и широко применяемых как профессиональными математиками, так и обычными людьми являются натуральные.

Определение

Натуральные числа – это те, которые принято использовать при обычном подсчете каких-либо материальных предметов, событий и вообще всего, что может быть воспринято органами чувств человека. С этим понятием мы сталкиваемся с детства, потому что этот вид чисел наиболее широко используется в обычной жизни. Люди не обращают внимание на то, как часто им приходится использовать натуральный ряд. Вот наглядный пример. Вряд ли кто задает себе вопрос: что такое натуральное число в математике, глядя на обычные часы, по которым мы определяем какое количество часов и минут прошло с момента начала текущих суток. Основная задача, которую выполняют такие числа, заключается в указании количества чего-либо.

Ряд натуральных чисел

Теперь, когда мы усвоили, что значит натуральное число, поговорим о конкретных примерах. Натуральный ряд начинается с числа 1, а для его обозначения используется буква N. Сам ряд представляет собой числовую последовательность, в которой каждое следующее число больше предыдущего на одну единицу.

Другими словами, натуральные числа — это хорошо знакомая нам последовательность. И какие числа в нее входят понять несложно, вот примеры таких чисел:

2, 31, 55, 74, 153, 1507.

А вот ряд, который образуют числа от 1 до 9:

1, 2, 3, 4, 5, 6, 7, 8, 9.

Поговорим про ноль

Относится ли 0 к натуральным числам? Прежде чем ответить на этот вопрос, вернемся к началу нашего изложения и вспомним, что значит натуральное число в математике. При обычном подсчете число 0 не применяют. Ведь он означает отсутствие чего-либо. Когда приходится констатировать факт, что мы чего-то не обнаружили, то никогда не употребляем словосочетания типа: 0 автомобилей или 0 бутылок. Вместо этого более привычной будет следующая фраза: «нет ни одной бутылки». Исходя из этого ответ на вопрос: входит ли 0 в натуральные числа, отпадает сам по себе. Однозначно, таковым его называть нельзя.

О самом большом числе

Как долго продолжается натуральный ряд? Числа в нем могут быть как одно- и двухзначными, так и трех-, четырехзначными и больше. Поэтому самое большое натуральное число в математике отсутствует, а ряд считают бесконечным.

• На заводе по производству метизов для автомобильной промышленности выпускается 1 563 800 крепежных болтов. Упомянутое число было использовано при подсчете выпущенной продукции, поэтому оно относится к ряду натуральных чисел.
• В астрономии при определении расстояний между небесными телами приходится сталкиваться с очень большими числами. Так размер большой полуоси орбиты Плутона составляет примерно 6 000 000 000 км.

Натуральные числа с нолями

С одной стороны, мы выяснили, что 0 не относится к натуральным числам. Но вполне естественно выглядит вопрос: 10 – натуральное число или нет? Безусловно, это число и любое другое с неограниченным количеством нолей относят к этому виду, потому что они могут применяться при подсчете или перечислении.

Действия, которые могут выполняться над натуральными числами

Над натуральными числами можно выполнять различные математические операции.

• Сложение. Два или более чисел являются слагаемыми, а результат действия называется суммой: 345 + 1 813 = 2 158
• Вычитание. Первое число, называемое уменьшаемым, должно быть больше другого, которое именуют вычитаемым. В результате получаем разность: 455 — 120 = 335
• Умножение. Два или более множителей, а в результате получается произведение: 36 х 3 = 108
• Деление. Первое число, которое будет делиться, называют делимым, второе – делителем, а результат – частным. Может быть с остатком или без него: 450:15=30, 450:20=22 + остаток 10.

Также существует степень натурального числа, а запись выглядит следующим образом: ab, где: а – основание степени, а b – показатель. Например, 3 2 = 9.

Разряды и натуральные числа

Разрядом называют место нахождения цифры в числе. Каждый разряд называется индивидуально, они располагаются по старшинству – справа налево и от младшего к старшему. Количество цифр числа совпадает с количеством разрядов.

Самым низшим из разрядов являются единицы, а самый старший всегда соответствует крайней левой цифре.

Например, число 5 469 содержит четыре разряда:

• 9 – разряд единиц,
• 6 – разряд десятков,
• 4 – разряд сотен,
• 5 – разряд тысяч.

Более высокие разряды называют:

Разряды объединяют в классы, каждый из которых включает три разряда:

Между классами для удобства чтения принято делать пробел.

Что такое натуральные значения в математике? Это любые значения, выраженные с использованием чисел натурального ряда. Еще один пример: 184 345 567 100 – в этом числе четыре класса: единицы, тысячи, миллионы и миллиарды.

Источник

Что такое Натуральное число

Определение натурального числа

Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.

Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.

Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.

Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.

Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).

Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.

Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.

Множество натуральных чисел

Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:

Натуральные числа:

Натуральные числа с нулём:

Ряд натуральных чисел

Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:

• это ряд натуральных чисел: 1, 2, 3, 4, 5, 6, 7, … ;
• это не является рядом натуральных чисел: 1, 2, 3, 5, 6, 7, … .

Наибольшего натурального числа не существует — натуральный ряд бесконечен.

Ненатуральные числа

Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).

Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;

• обычные дроби, например: ½, –¾;
• десятичные дроби, например: 0.07;
• иррациональные числа, например: π (≈3.14), e (≈2.718), √2 (≈1.4142).

Свойства натуральных чисел

Натуральные числа обладают следующими свойствами:

• множество натуральных чисел (обычно) начинается с 1, в нём находятся все натуральные числа и оно бесконечно;
• за каждым натуральным числом всегда следует одно, и только одно натуральное число, которое больше предыдущего на 1;
• результатом деления натурального числа на 1, является само натуральное число: a / 1 = a ; например: 4 / 1 = 4;
• результатом деления натурального числа на него самого будет 1: a / a = 1 ; например: 5 / 5 = 1;
• переместительный закон сложения: a + b = b + a ; например: 1 + 2 = 2 + 1;
• сочетательный закон сложения: (a + b) + c = a + (b + c) ; например: (1 + 2) + 3 = 1 + (2 + 3);
• переместительный закон умножения: ab = ba ; например: 2×3 = 3×2,
• сочетательный закон умножения: (a × b) × c = a × (b × c) ; например: (1 × 2) × 3 = 1 × (2 × 3);
• распределительный закон умножения относительно сложения: a × (b + c) = ab + ac ; например: 2 × (3 + 4) = 2×3 + 2×4;
• распределительный закон умножения относительно вычитания: a × (b – c) = ab – ac ; например: 2 × (4 – 3) = 2×4 – 2×3;
• распределительный закон деления относительно сложения: (a + b) : c = a:c + b:c; например: (4 + 6) : 2 = 4:2 + 6:2
• распределительный закон деления относительно вычитания: (a – b) : c = a:c – b:c; например: (6 – 4) : 2 = 6:2 – 4:2;

Источник

Натуральные числа. Ряд натуральных чисел.

История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.

Натуральные числа – это числа которые мы используем при счете предметов.

Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….

Нуль не относится к натуральным числам.

Все натуральные числа или назовем множество натуральных чисел обозначается символом N.

Таблица натуральных чисел.

Натуральный ряд.

Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.

Свойства натурального ряда:

• Наименьшее натуральное число – единица.
• У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
• Натуральный ряд не имеет наибольшего числа, он бесконечен.

Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5

Пример №2:
Нуль является натуральным числом?
Ответ: нет.

Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.

Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.

Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.

Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.

Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.

Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.

Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.

Источник

Натуральные числа

Множество натуральных чисел принято обозначать символом N (от лат. naturalis — естественный).

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

• Наименьшее натурально число — единица ( 1 )
• Наибольшего натурального числа не существует.
• Нуль ( 0 ) не является натуральным числом.

Множество натуральных чисел бесконечно, так как для любого числа n всегда найдется число m , которое больше n

Из соседних натуральных чисел, число, которое стоит левее числа n называется предыдущим числу n , а число, которое стоит правее называется следующим за n .

Операции над натуральными числами

К замкнутым операциям над натуральными числами (операциям в результате, которых получается натуральных чисел) относятся следующие арифметические операции:

• Сложение
• Умножение
• Возведение в степень a b , где a — основание степени и b — показатель степени. Если основание и показатель — натуральные числа, то и результат будет являться натуральным числом.

Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как их результат не всегда будет натуральным числом.

• Вычитание (При этом Уменьшаемое должно быть больше Вычитаемого)
• Деление

Классы и разряды

Низший разряд — самый правый. Старший разряд — самый левый.

Низший разряд — единицы, далее — десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллионы, десятки миллионов и т.д.

5 — единиц, 0 — десятков, 7 — сотен,
2 — тысячи, 4 — десятков тысяч, 8 — сотен тысяч,
3 — миллиона, 5 — десятков миллионов, 1 — сотня миллионов

Для удобства чтения, натуральных числа разбивают, на группы по три цифры в каждой начиная справа.

Класс — группа из трех цифр, на который разбито число, начиная справа. Последний класс может состоять из трех, двух или одной цифры.

• Первый класс — класс единиц;
• Второй класс — класс тысяч;
• Третий класс — класс миллионов;
• Четвертый класс — класс миллиардов;
• Пятый класс — класс триллионов;
• Шестой класс — класс квадрильонов (квадриллионов);
• Седьмой класс — класс квинтильонов (квинтиллионов);
• Восьмой класс — класс секстильонов;
• Девятый класс — класс септильонов;

34 — миллиарда 456 миллионов 196 тысяч 45

Сравнение натуральных чисел

Сравнение натуральных чисел с разным количеством цифр

Сравнение натуральных чисел с равным количеством цифр

3466 &gt 346 — так как число 3466 состоит из 4 цифр, а число 346 из 3 цифр.

34666 &lt 245784 — так как число 34666 состоит из 5 цифр, а число 245784 из 6 цифр.

346 667 670 5 2 6 986

346 667 670 5 6 9 429

Второе из натуральных чисел с равным количеством цифр больше, так как 6 > 2.

Источник

Что такое натуральные числа

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.

С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.

Натуральные числа — это.

Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.

Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).

Само слово «naturalis» в переводе с латинского означает «естественный».

А вот если взять, к примеру, дробные числа (0.5, 13.856, 1/5 и так далее) и уж тем более отрицательные (-1, -5, -100), то в них весьма мало естественности. А значит, можно дать и другое, более простое определение натуральных чисел.

Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.

Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.

А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.

И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».

Натуральный ряд

Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.

Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.

И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».

Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.

Это записано в основном законе натуральных чисел:

Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.

Ноль — это натуральное число или нет

Натуральный ряд можно построить двумя способами:

1. из чисел, которые обозначают нумерацию предметов (первый, второй, третий, четвертый и так далее);
2. из чисел, которые обозначают количество предметов (один, два, три, четыре и так далее).

Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.

То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.

Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.

Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.

Операции с натуральными числами

Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:

1. Сложение. Слагаемое + Слагаемое = Сумма. И если слагаемые натуральные числа, то и сумма будет натуральным числом.
2. Вычитание. Уменьшаемое – Вычитаемое = Разность. Принцип натуральности чисел точно такой же.
3. Умножение. Множитель * Множитель = Произведение. При перемножении натуральных чисел получаем натуральное число.
4. Деление. Делимое / Делитель = Частное. В данном случае при делении натуральных чисел результат не обязательно должен быть натуральным числом. Возможен и дробный вариант. И еще главное правило – нельзя делить на ноль.

Вот и все, что мы хотели рассказать о натуральных числах.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.

Источник