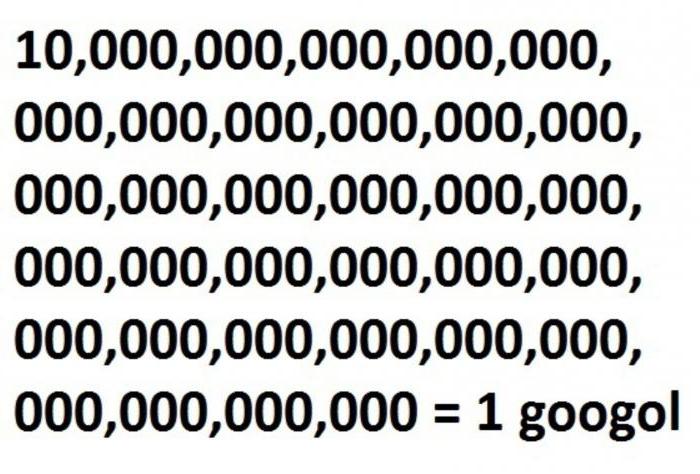Что значит наименьшее числовое значение

Какое наибольшее число? Наибольшее и наименьшее число

Когда человек только учился считать, ему хватало пальцев рук, чтобы определить, что два мамонта, гуляющие у пещеры, это меньше, чем то стадо за горой. Но как только он осознал, что такое позиционное счисление (когда число имеет конкретное место в длинном ряду), он стал задумываться: а что дальше, каково наибольшее число?

Многоточие в конце ряда

Когда школьников знакомят с первоначальным понятием натуральных чисел, по краям ряда чисел благоразумно ставят многоточие и объясняют, что наибольшее и наименьшее число — это категория бессмысленная. Всегда есть возможность к самому большому числу прибавить единицу, и оно уже не будет самым большим. Но прогресс не был бы возможен, если бы не было тех, кто захотел найти смысл там, где его быть не должно.

Бесконечность числового ряда, кроме пугающего и неопределенного философского значения, создавала и чисто технические трудности. Приходилось искать обозначения для очень больших чисел. Сначала это делалось отдельно для основных языковых групп, а с развитием глобализации появились слова, именующие наибольшее число, общепринятые во всем мире.

Десять, сто, тысяча

В каждом языке для чисел, имеющих практическое значение, найдено собственное название.

В русском прежде всего это ряд от нуля до десяти. До сотни дальнейшие числа называются или на их основе, с небольшим изменением корней – «двадцать» (два по десять), «тридцать» (три по десять) и т. д., или являются составными: «двадцать один», «пятьдесят четыре». Исключение – вместо «четыредцать» мы имеем более удобное «сорок».

Наибольшее двузначное число — «девяносто девять» — имеет составное название. Далее из собственных традиционных названий — «сто» и «тысяча», остальные образованы из нужных сочетаний. Похожая ситуация в других распространенных языках. Логично думать, что устоявшиеся имена давались числам и цифрам, с которыми имели дело большинство обычных людей. Даже что такое тысяча голов скота, мог представить и обычный крестьянин. С миллионом было сложнее, и началась путаница.

Миллион, квинтиллион, дециллиард

В середине XV века французом Николя Шуке для того, чтобы обозначить самое наибольшее число, была предложена система наименования на основе числительных из общепринятой среди ученых латыни. В русском языке они претерпели некоторую модификацию для удобства произношения:

• 1 – Unus – ун.
• 2 – Duo, Bi (двойной) – дуо, би.
• 3 – Tres – три.
• 4 — Quattuor – квадри.
• 5 – Quinque – квинти.
• 6 – Sex – сексти.
• 7 – Septem – септи.
• 8 — Octo – окти.
• 9 – Novem – нони.
• 10 – Decem – деци.

Основой названий должно было стать -иллион, от «миллион» – «большая тысяча» — т. е. 1 000 000 – 1000^2 — тысяча в квадрате. Это слово, чтобы упомянуть наибольшее число, впервые употребил знаменитый мореход и ученый Марко Поло. Так, тысяча в третьей степени стала триллионом, 1000^4 – квадриллионом. Другой француз – Пелетье — предложил для чисел, которые у Шюке назывались «тысяча миллионов» (10^9), «тысяча биллионов» (10^15) и т. д., использовать окончание «-иллиард». Получилось, что 1 000 000 000 – это миллиард, 10^15 – биллиард, единица с 21 нулём – триллиард и так далее.

Терминология французских математиков стала использоваться во многих странах. Но постепенно выяснилось, что 10^9 в некоторых трудах стали именовать не миллиардом, а биллионом. А в США приняли систему, по которой окончание -иллион получили степени не миллиона, как у французов, а тысячи. В результате сегодня в мире действуют две шкалы: «длинная» и «короткая». Чтобы понять, какое число имеется в виду под наименованием, например, квадриллион, лучше уточнить в какую степень возведено число 10. Если в 15-ю, — это «короткая» шкала, принятая в США, Канаде, Великобритании и ряде других стран, в том числе в России (правда, у нас 10^9– не биллион, а миллиард), если в 24 – это «длинная», принятая в большинстве регионов мира.

Тредециллион, вигинтиллиард и миллеиллион

После того как будет использовано последнее числительное – деци, и образуется дециллион – самое наибольшее число без сложных словообразований — 10^33 по короткой шкале, для следующих разрядов используются сочетания нужных префиксов. Получаются сложные составные названия типа тредециллион— 10^42, квиндециллион — 10^48 и т. д. Несоставных, собственных наименований у римлян удостоились: двадцать – viginti, сто – centum и тысяча – mille. Следуя правилам Шюке, можно бесконечно долго образовывать названия-монстры. Например, число 10 ^308760 называется дуцентдуомилианонгентновемдециллион.

Но эти построения интересны только ограниченному числу людей — они не используются в практике, да и сами эти величины не привязаны даже к теоретическим задачам или теоремам. Именно для сугубо теоретических построений предназначены числа-великаны, получавшие иногда очень звучные имена или называемые по фамилии автора.

Тьма, легион, асанкхейя

Вопрос огромных чисел волновал и «докомпьютерные» поколения. У славян существовали несколько систем счисления, в некоторых они добирались до огромных высот: наибольшее число — 10^50. Названия чисел с высоты нашего времени кажутся поэзией, а во всех ли в них был практический смысл, знают только историки и лингвисты: 10^4 – «тьма», 10^5 – «легион», 10^6 – «леодр», 10^7 – вран, ворон, 10^8 – «колода».

Не менее красивое по названию число asaṃkhyeya упоминается в буддийских текстах, в древнекитайских и древнеиндийских собраниях сутр.

Гугол, гуголплекс

Математик из Колумбийского университета (США) Edward Kasner с начала 1920 годов начал задумываться о больших числах. В частности, его интересовало звучное и выразительное название для красивого числа 10^100. Однажды он гулял с племянниками и рассказал им об этом числе. Девятилетний Милтон Сиротта предложил слово googol — гугол. Дядя получил от племянников и бонус – новое число, которое они объяснили так: единица и столько нулей, сколько можешь написать, пока совсем не устанешь. Имя этому числу было гуголплекс. Поразмыслив, Кашнер решил, что это будет число 10^googol.

Смысл в таких числах Кашнер видел больше педагогический: наука тогда не знала чего-либо в таком количестве, а будущим математикам на их примере он объяснял, какое наибольшее число может сохранять отличие от бесконечности.

Шикарную идею маленьких гениев нейминга оценили основатели компании по продвижению нового поисковика. Домен googol оказался занят, и буква o выпала, зато появилось название, для которого эфемерное число может стать когда-нибудь реальным — столько будут стоить его акции.

Число Шеннона, число Скьюза, медзон, мегистон

В отличие от физиков, периодически натыкающихся на ограничения, налагаемые природой, математики продолжают путь в сторону бесконечности. Любитель шахматной игры Клод Шеннон (1916-2001) наполнил смыслом число 10^118 — именно столько вариантов позиций может возникнуть в течении 40 ходов.

Стенли Скьюз из Южной Африки занимался одной из семи задач, входящих в список «проблем тысячелетия» — гипотезой Римана. Она касается поиска закономерности в распределении простых чисел. В ходе рассуждений он использовал сначала число 10^10^10^34, обозначенное им Sk₁ , а затем 10^10^10^963 — второе число Скьюза — Sk₂.

Для оперирования такими числами не подходит даже привычная система записи. Гуго Штейнгауз (1887-1972) предложил использовать геометрические фигуры: n в треугольнике – это n в степени n, n в квадрате – n в n треугольниках, n в круге — это n в n квадратах. Он объяснял эту систему на примере чисел мега – 2 в круге, медзон – 3 в круге, мегистон – 10 в круге. Так трудно обозначить, например, наибольшее двузначное число, но оперировать колоссальными величинами стало проще.

Профессор Дональд Кнут предложил стрелочную нотацию, в которой повторное возведение в степень обозначалось стрелкой, заимствованной из практики программистов. Гугол в этом случае выглядит как 10↑10↑2, а гуголплекс — 10↑10↑10↑2.

Число Грэма

Рональд Грэм (р. 1935) американский математик, в ходе исследования теории Рамсея, связанной с гиперкубами — многомерными геометрическими телами – ввел особые числа G₁ – G₆₄ , с помощью которых он обозначил границы решения, где верхним пределом стало наибольшее кратное число, получившее его имя. Он вычислил даже 20 последних цифр, а исходными данными послужили следующие значения:

— G₂= 3↑…↑3 (число стрелок сверхстепени = G₁).

— G₃= 3↑…↑3 (число стрелок сверхстепени = G₂).

— G₆₄= 3↑…↑3 (число стрелок сверхстепени = G₆₃ )

G₆₄, обозначаемое просто G, и является самым большим в мире числом, использованным в ходе математических вычислений. Оно занесено в книгу рекордов.

Источник

Урок 9 Бесплатно Меньше или больше

Вы уже знаете, что такое натуральное число и как оно записывается.

Также Вам известно, что такое координатный луч.

Сегодня мы применим эти знания, чтобы сформулировать понятия “больше” и “меньше” для натуральных чисел, научимся отвечать на вопрос, как соотносятся два натуральных числа.

Узнаем, как сравнивать числа с помощью координатного луча, как сравнивать натуральные числа с одинаковым и разным количеством знаков, разберем понятие “сортировка” для чисел.

Определение

Вспомним, как выглядит натуральный ряд:

1, 2, 3, 4, 5, 6, 7, 8, 9 …

Из двух натуральных чисел больше то, которое при счете называют позже.

Из двух натуральных чисел меньше то, которое при счете называют раньше.

Данное определение достаточно просто и понятно, посмотрим на примерах.

Например, как соотносятся 3 и 5?

Если мы посмотрим на натуральный ряд, то увидим, что 3 названо раньше, чем 5, следовательно, 3 меньше 5-ти.

Другой пример, как соотносятся числа 9 и 6?

Опять же, надо посмотреть на натуральный ряд, тогда можно увидеть, что 9 названо позже, чем 6, значит, 9 больше 6-ти.

Каждый раз писать словами “больше” или “меньше” может быть неудобно, поэтому удобно использовать знаки.

Знак “ ” читается как “больше”.

Таким образом, чтобы кратко записать, что 3 меньше 5-ти, достаточно написать “\(\mathbf<3 6>\)”.

Запись с использование знаком “больше” или “меньше” называют неравенством.

Довольно часто вопрос про соотношение двух чисел может ставится так: “какой знак должен стоять в неравенстве на месте пропуска”, а дальше идет неравенство с пропущенным знаком, например, такое: “4 _ 6”.

В данном случае надо ответить на вопрос, больше ли 4 6-ти или меньше, и поставить соответствующий знак.

Здесь первое число меньше второго и нужно поставить знак “ 0”, “2 > 0”, “3 > 0” и так далее для каждого натурального числа.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Значение слова «наименьший»

НАИМЕ́НЬШИЙ, —ая, —ее. Самый меньший, самый малый. Наибольшая его [острова] ширина равняется 125, а наименьшая 25 верстам. Чехов, Остров Сахалин.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

НАИМЕ’НЬШИЙ, ая, ее (книжн.). Самый малый. Прямая линия есть наименьшее расстояние между двумя точками. Наименьшее кратное.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

наиме́ньший

1. самый небольшой, незначительный ◆ Наибольшее число людей может объединить только наименьший общий знаменатель. Фридрих фон Хайек

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова ретрансляционный (прилагательное):

Синонимы к слову «наименьший&raquo

Предложения со словом «наименьший&raquo

• Вместо того чтобы настоять и, если нужно, за руку отвести, мы всегда выбираем путь наименьшего сопротивления.

Цитаты из русской классики со словом «наименьший»

• Складываясь в эти соединения, люди всегда становятся между собой в такое отношение, что наибольшее количество людей принимают наибольшее прямое участие и наименьшее количество людей — наименьшее прямое участие в том совокупном действии, для которого они складываются.

Сочетаемость слова «наименьший&raquo

Понятия со словом «наименьший»

Афоризмы русских писателей со словом «наименьший&raquo

• Я — за изучение именно литературной техники, то есть грамотности, то есть умения затрачивать наименьшее количество слов для достижения наибольшего количества эффекта, наибольшей простоты, пластичности и картинности изображаемых словами вещей, лиц, пейзажей, событий — вообще явлений социального бытия.

Отправить комментарий

Дополнительно

Предложения со словом «наименьший&raquo

Вместо того чтобы настоять и, если нужно, за руку отвести, мы всегда выбираем путь наименьшего сопротивления.

Если мы попадаем в ситуацию, которая потенциально может стать неудобной в результате нашего отказа, мы выбираем путь наименьшего сопротивления.

На этом уровне задача не управлять, а понести наименьшие потери и получить максимальный опыт.

Синонимы к слову «наименьший&raquo

Сочетаемость слова «наименьший&raquo

Морфология

Правописание

Карта слов и выражений русского языка

Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.

Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.

Сайт оснащён мощной системой поиска с поддержкой русской морфологии.

Источник