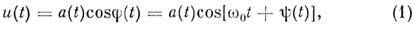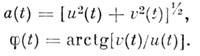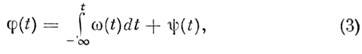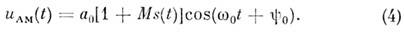Физическая энциклопедия. В 5-ти томах
МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ
МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ — колебания, параметры к-рых (амплитуда, фаза, частота, длительность и т. п.) изменяются во времени. Это понятие распространяется и на колебания, параметры к-рых изменяются в пространстве, тогда говорят о пространственно модулированных колебаниях; в отличие от временных M. к. они могут быть дву- и трёхмерными. Далее всюду речь идёт только о колебаниях, модулированных во времени. Характер исходных (несущих) колебаний и законы их модуляции разнообразны: от простейших гармонических до хаотических. Это могут быть даже не колебательные, а, напр., импульсные сигналы с переменными длительностью, скважностью или другими характерными для импульсной модуляции параметрами.
Простейшим примером M. к., имеющим принципиальное значение для описания мн. физ. процессов и техн. приложений, является квазигармонич. M. к.:
где a(t) — мгновенная амплитуда, j(t) — полная фаза колебаний, w 0 = const — несущая частота, y(t) — фаза колебаний. Все эти величины вводят но аналогии с обычными гармонич. колебаниями, для к-рых a(t) = const и y(t) = const. B произвольном случае представление (1) неоднозначно: множеству пар a(t),f(t) соответствует одна и та же ф-ция u(t), что затрудняет строгий анализ M. к. Обычно эту неоднозначность удаётся устранить и оперировать с амплитудами и фазами как с определ. параметрами M. к. В частности, одним из эвристич. способов устранения неоднозначности является введение дополнит. сигнала u(t), каждая фурье-составляющая к-рого сдвинута по фазе па p/2 относительно соответствующей фурье-составляющей осн. сигнала u(t )(преобразование Гильберта), что приводит к образованию т. н. аналитического сигнала:
амплитуда a(t )и фаза f(t) к-рого однозначно выражаются через u(t) и u(t):
Физически это соответствует мысленной замене осцилляторов ротаторами. Во мн. техн. устройствах, реализующих, напр., приём M. к., преобразование (2) используют как наиболее эфф. «средство» демодуляции.
Интерпретации M. к. как в исходной (1), так и в обобщённой (2) форме совпадают, если предположить медленность изменения ф-ций a(t )и f(t) на протяжении периода T несущей частоты w 0 = 2p/T и пренебречь усреднённым вкладом высших составляющих спектра. Как правило, именно с таким квазигармонич. M. к. приходится иметь дело в технике.
Виды M. к. Итак, в определ. условиях [медленность изменения и (или) возможность доопределения] M. к. можно разделить на амплитудно-модулированные колебания (AMK) и фазомодулированные колебания (ФМК). Последние называют иногда также колебаниями с угл. модуляцией, выделяя среди них частотно-модулированные колебания (ЧМК) и собственно ФМК. Тем не менее, поскольку
точных критериев различения режимов, в к-рых w(t) = const, . y(t) 
const и y(t) = const, w(t) 
const, не существует. Поэтому при проведении такой классификации руководствуются скорее нек-рой «спектральной интуицией», а главное принципами реализации процессов модуляции и демодуляции в соответствующих техн. устройствах.
Квазигармонич. AMK обычно записывают в виде:
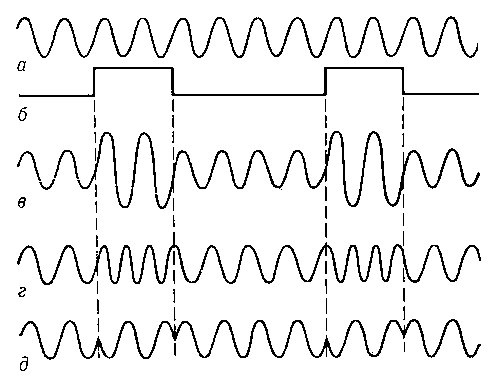
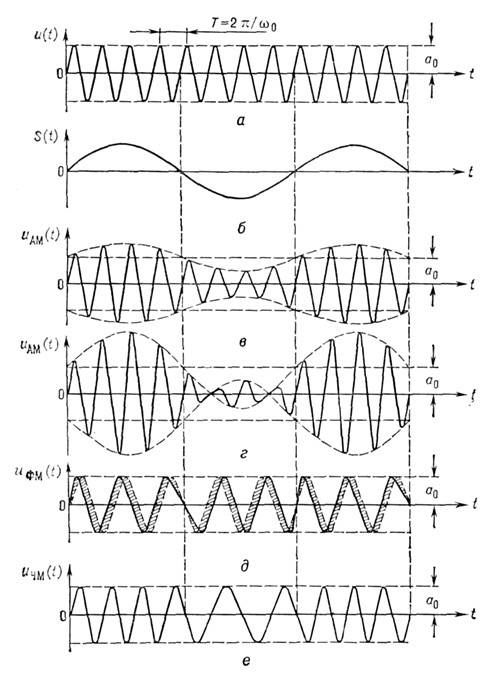
Здесь а 0 — пост. амплитуда несущего колебания (рис., a), s(t) — нормированный [обычно mах|s(t)| =1] модулирующий сигнал (рис., б), M- коэф. модуляции (см. Амплитудная модуляция). Случай M 1 наз. перемодулированными (рис., г). При использовании AMK в приёмопередающих системах (вещание, связь и т. п.) выбирают оптимальные (с точки зрения эфф. использования мощности передатчиков и нелинейных искажений формы AMK) значения M. Поскольку передаваемая информация равнозначно заключена в верхних и нижних боковых составляющих спектра AMK, то выгодно формировать и передавать информацию AMK с подавлением одной из групп боковых частот (полос). В этом случае получаются т. фм , K чм — коэф., характеризующие девиацию фа-за Df и частоты Dw (рис, д, е). В силу соотношения (3) ф-лы (5) и (6) взаимно связаны, что и позволяет счи-тать ЧМК разновидностью ФМК и наоборот.
Модулированные колебания: a — несущее (немодулированное) колебание; б — гармоническое модулирующее колебание; в — амплитудно-модулированное колебание; г — перемодулирован-чое колебание; д — фазо-модулированное колебание; е- частотно-модулированное колебание.
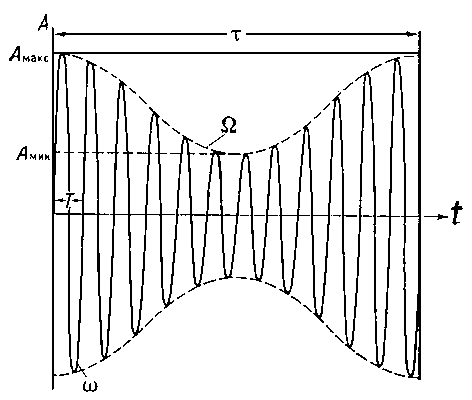
Спектры ФМК и ЧМК (см. Частотная модуляция, Фазовая модуляция )существенно сложнее спектра AMK даже в случае гармонич. модуляции и в значит. мере определяются значением индекса модуляции т= Dw/W, характеризующего отношение девиации частоты к частоте W модулирующего сигнала. При т >> 1(а именно такие значения обычно используют в системах связи) ширина спектра ЧМК равна удвоенной девиации частоты 2Dw = 2mW, тогда как спектр AMK занимает полосу ширины 2W, т. е. в то раз меньшую. Причём для ЧМК девиация частоты пропорц. амплитуде модулирующего сигнала Dw чм и не зависит от частоты W, а для ФМК, в силу (3), Dw фм пропорциональна W. Большая «широкополосность» ЧМК и ФМК часто (но не всегда, исключение составляют, напр., случаи оптим. приёма) обусловливает их большую помехоустойчивость по сравнению с AMK.
Др. важными видами M. к., встречающимися в технике и природе, являются колебания, модулированные как по амплитуде, так и по фазе (частоте), а также импульсно-модулиров. колебания — последовательности импульсов с ВЧ-заполнением (см. Импульсная мо-дуляция).
Применения M. к. Фактически все сигналы, используемые в технике и возникающие в естеств. условиях, можно считать M. к. В технике связи, напр., модулирующие сигналы являются информационными, т. е. содержащими передаваемую информацию, тогда как несущее колебание, частота к-рого, как правило много больше ширины спектра информац. сигнала, обеспечивает более эфф. передачу этой информации на расстояние При этом огибающая AMK подвергается случайным изменениям и на трассе распространения и в приёмопередающей аппаратуре (т. е. обладает слабой помехозащищённостью, в особенности в области НЧ), поэтому применение AMK целесообразно там, где важна простота устройств связи и характер сообщения может не пострадать из-за отсутствия или искажения НЧ-компонент спектра. Так, в телевидении для передачи изображения используют однополосные AMK, а для передачи НЧ-спектра звукового сопровождения применяют более помехоустойчивые ЧМК. У ЧМК, однако более широкий спектр по сравнению с AMK, в особенности когда индекс модуляции выбран большим для ослабления действия помех и повышения точности передачи сообщения, что снижает эффективность использования рабочего диапазона частот при ограниченном числе каналов связи.
В радиолокации и радиоастрономии M. к. используют для обнаружения целей и определения их важнейших геом. (размеры, конфигурация) и физ. (темп-ра, плотность, диэлектрич. проницаемость и т. п.) параметров. Для физ. сред характерно появление естеств. модуляции, возникающей при воздействии магн. или электрич полей на излучающие материальные среды (см Зеемана эффект, Штарка эффект); при рассеянии света на колебаниях кристаллич. решётки твёрдых тел ( Мандельштама- Бриллюэна рассеяние )и т. д. Понятие естеств. модуляции распространяют также на волны. Так, напр., волновой пучок достаточной интенсивности может изменять параметры среды и, как следствие, модулировать свою плотность (см. Самофо-кисировка света). При распространении волн в нелинейных диспергирующих средах (жидкостях, плазме) возникает явление автомодуляции волн, связанное с разл. видами неустойчивости волн по отношению к НЧ-пространственно-временным возмущениям. Естеств модуляция находит практич. приложение в радио- и оптич. спектроскопии для диагностики параметров разнообразных сред; в нелинейной оптике для формирования мощных световых потоков; в акустике и др областях прикладной физики. Способы практич. реализации M. к. связаны, как правило, с нелинейными устройствами, параметры к-рых (в радиотехнике, напр., это ёмкость, сопротивление; в акустике — плотность, и т. п. ) можно изменять во времени в соответствии с законом модуляции. Техн. устройства, реализующие M. к., наз. модуляторами.
Лит.: Pытов С. M., Модулированные колебания и вол-ны, «Тр. ФИАН», 1940, т. 2, в. 1; Fренкс Л., Теория сигна-лов, пер. с англ. M., 1974; Баскаков С. И., Радиотехниче-ские цепи и сигналы, M., 1983; Вайнштейн Л. А., Вак-ман Д. E., Разделение частот в теории колебаний и волн, M., 1983. Ю. К. Богатырёв, M. А. Миллер.
Источник
Модуляция колебаний
Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .
Полезное
Смотреть что такое «Модуляция колебаний» в других словарях:
МОДУЛЯЦИЯ КОЛЕБАНИЙ — медленное по сравнению с периодом колебаний изменение амплитуды, частоты или фазы колебаний по определ. закону. Соответственно различаются амплитудная, частотная и фазовая М. к. (рис. 1). Возможна и смешанная модуляция (напр., амплитудно фазовая) … Физическая энциклопедия
МОДУЛЯЦИЯ КОЛЕБАНИЙ — изменение амплитуды, частоты, фазы или др. характеристик колебаний по заданному закону, медленное по сравнению с периодом этих колебаний. Различают модуляцию колебаний амплитудную, частотную и фазовую. Модуляция колебаний используется для… … Большой Энциклопедический словарь
МОДУЛЯЦИЯ КОЛЕБАНИЙ — изменение разл. характеристик колебаний, медленное по сравнению с их периодом (см. Модулированные колебания). Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
модуляция колебаний — изменение амплитуды, частоты, фазы или других характеристик колебаний по заданному закону, медленное по сравнению с периодом этих колебаний. Различают модуляцию колебаний амплитудную, частотную и фазовую. Модуляция колебаний используется для… … Энциклопедический словарь
МОДУЛЯЦИЯ КОЛЕБАНИЙ — изменение амплитуды, частоты, фазы или др. характеристик колебаний по заданному закону, медленное по сравнению с периодом этих колебаний. Различают М.к. амплитудную, частотную и фазовую. М. к. используется для передачи информации с помощью эл.… … Естествознание. Энциклопедический словарь
МОДУЛЯЦИЯ СВЕТА — (модуляция оптического излучения), изменение во времени по заданному закону амплитуды (интенсивности), частоты, фазы или поляризации колебаний оптического излучения. Применяется для передачи информации с помощью оптич. сигналов или для… … Физическая энциклопедия
Модуляция света — Модуляция колебаний электромагнитного излучения оптического диапазона (видимого света, ультрафиолетового и инфракрасного излучений). При М. с. изменяются амплитуда (и следовательно, интенсивность), фаза, частота или поляризация световых… … Большая советская энциклопедия
МОДУЛЯЦИЯ — (от лат. modulatio мерность, размеренность), изменение по заданному закону во времени параметров, характеризующих к. л. стационарный физ. процесс. Примеры М.: изменение по определ. закону амплитуды, частоты или фазы гармонич. колебания для… … Физическая энциклопедия
Модуляция (в физике) — Модуляция (от лат. modulatio мерность, размеренность) в физике и технике, изменение по заданному закону во времени величин, характеризующих какой либо регулярный процесс. М. вызывают внешним воздействием. Наибольшее практическое значение имеет М … Большая советская энциклопедия
МОДУЛЯЦИЯ — в физике изменение по заданному закону во времени величин, характеризующих какой либо регулярный физический процесс. Практическое значение имеет модуляция колебаний … Большой Энциклопедический словарь
Источник
МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ
— колебания, параметры к-рых (амплитуда, фаза, частота, длительность и т. п.) изменяются во времени. Это понятие распространяется и на колебания, параметры к-рых изменяются в пространстве, тогда говорят о пространственно модулированных колебаниях; в отличие от временных M. к. они могут быть дву- и трёхмерными. Далее всюду речь идёт только о колебаниях, модулированных во времени. Характер исходных (несущих) колебаний и законы их модуляции разнообразны: от простейших гармонических до хаотических. Это могут быть даже не колебательные, а, напр., импульсные сигналы с переменными длительностью, скважностью или другими характерными для импульсной модуляции параметрами.
Простейшим примером M. к., имеющим принципиальное значение для описания мн. физ. процессов и техн. приложений, является квазигармонич. M. к.:
где a(t) — мгновенная амплитуда, j(t) — полная фаза колебаний, w 0 = const — несущая частота, y(t) — фаза колебаний. Все эти величины вводят но аналогии с обычными гармонич. колебаниями, для к-рых a(t) = const и y(t) = const. B произвольном случае представление (1) неоднозначно: множеству пар a(t),f(t) соответствует одна и та же ф-ция u(t), что затрудняет строгий анализ M. к. Обычно эту неоднозначность удаётся устранить и оперировать с амплитудами и фазами как с определ. параметрами M. к. В частности, одним из эвристич. способов устранения неоднозначности является введение дополнит. сигнала u(t), каждая фурье-составляющая к-рого сдвинута по фазе па p/2 относительно соответствующей фурье-составляющей осн. сигнала u(t )(преобразование Гильберта), что приводит к образованию т. н. аналитического сигнала:
амплитуда a(t )и фаза f(t) к-рого однозначно выражаются через u(t) и u(t):
Физически это соответствует мысленной замене осцилляторов ротаторами. Во мн. техн. устройствах, реализующих, напр., приём M. к., преобразование (2) используют как наиболее эфф. «средство» демодуляции.
Интерпретации M. к. как в исходной (1), так и в обобщённой (2) форме совпадают, если предположить медленность изменения ф-ций a(t )и f(t) на протяжении периода T несущей частоты w 0 = 2p/T и пренебречь усреднённым вкладом высших составляющих спектра. Как правило, именно с таким квазигармонич. M. к. приходится иметь дело в технике.
Виды M. к. Итак, в определ. условиях [медленность изменения и (или) возможность доопределения] M. к. можно разделить на амплитудно-модулированные колебания (AMK) и фазомодулированные колебания (ФМК). Последние называют иногда также колебаниями с угл. модуляцией, выделяя среди них частотно-модулированные колебания (ЧМК) и собственно ФМК. Тем не менее, поскольку
точных критериев различения режимов, в к-рых w(t) = const, . y(t) 
const и y(t) = const, w(t) 
const, не существует. Поэтому при проведении такой классификации руководствуются скорее нек-рой «спектральной интуицией», а главное принципами реализации процессов модуляции и демодуляции в соответствующих техн. устройствах.
Квазигармонич. AMK обычно записывают в виде:
Здесь а 0 — пост. амплитуда несущего колебания (рис., a), s(t) — нормированный [обычно mах|s(t)| =1] модулирующий сигнал (рис., б), M- коэф. модуляции (см. Амплитудная модуляция). Случай M 1 наз. перемодулированными (рис., г). При использовании AMK в приёмопередающих системах (вещание, связь и т. п.) выбирают оптимальные (с точки зрения эфф. использования мощности передатчиков и нелинейных искажений формы AMK) значения M. Поскольку передаваемая информация равнозначно заключена в верхних и нижних боковых составляющих спектра AMK, то выгодно формировать и передавать информацию AMK с подавлением одной из групп боковых частот (полос). В этом случае получаются т. фм , K чм — коэф., характеризующие девиацию фа-за Df и частоты Dw (рис, д, е). В силу соотношения (3) ф-лы (5) и (6) взаимно связаны, что и позволяет счи-тать ЧМК разновидностью ФМК и наоборот.
Модулированные колебания: a — несущее (немодулированное) колебание; б — гармоническое модулирующее колебание; в — амплитудно-модулированное колебание; г — перемодулирован-чое колебание; д — фазо-модулированное колебание; е— частотно-модулированное колебание.
Спектры ФМК и ЧМК (см. Частотная модуляция, Фазовая модуляция )существенно сложнее спектра AMK даже в случае гармонич. модуляции и в значит. мере определяются значением индекса модуляции т= Dw/W, характеризующего отношение девиации частоты к частоте W модулирующего сигнала. При т >> 1(а именно такие значения обычно используют в системах связи) ширина спектра ЧМК равна удвоенной девиации частоты 2Dw = 2mW, тогда как спектр AMK занимает полосу ширины 2W, т. е. в то раз меньшую. Причём для ЧМК девиация частоты пропорц. амплитуде модулирующего сигнала Dw чм и не зависит от частоты W, а для ФМК, в силу (3), Dw фм пропорциональна W. Большая «широкополосность» ЧМК и ФМК часто (но не всегда, исключение составляют, напр., случаи оптим. приёма) обусловливает их большую помехоустойчивость по сравнению с AMK.
Др. важными видами M. к., встречающимися в технике и природе, являются колебания, модулированные как по амплитуде, так и по фазе (частоте), а также импульсно-модулиров. колебания — последовательности импульсов с ВЧ-заполнением (см. Импульсная мо-дуляция).
Применения M. к. Фактически все сигналы, используемые в технике и возникающие в естеств. условиях, можно считать M. к. В технике связи, напр., модулирующие сигналы являются информационными, т. е. содержащими передаваемую информацию, тогда как несущее колебание, частота к-рого, как правило много больше ширины спектра информац. сигнала, обеспечивает более эфф. передачу этой информации на расстояние При этом огибающая AMK подвергается случайным изменениям и на трассе распространения и в приёмопередающей аппаратуре (т. е. обладает слабой помехозащищённостью, в особенности в области НЧ), поэтому применение AMK целесообразно там, где важна простота устройств связи и характер сообщения может не пострадать из-за отсутствия или искажения НЧ-компонент спектра. Так, в телевидении для передачи изображения используют однополосные AMK, а для передачи НЧ-спектра звукового сопровождения применяют более помехоустойчивые ЧМК. У ЧМК, однако более широкий спектр по сравнению с AMK, в особенности когда индекс модуляции выбран большим для ослабления действия помех и повышения точности передачи сообщения, что снижает эффективность использования рабочего диапазона частот при ограниченном числе каналов связи.
В радиолокации и радиоастрономии M. к. используют для обнаружения целей и определения их важнейших геом. (размеры, конфигурация) и физ. (темп-ра, плотность, диэлектрич. проницаемость и т. п.) параметров. Для физ. сред характерно появление естеств. модуляции, возникающей при воздействии магн. или электрич полей на излучающие материальные среды (см Зеемана эффект, Штарка эффект); при рассеянии света на колебаниях кристаллич. решётки твёрдых тел ( Мандельштама— Бриллюэна рассеяние )и т. д. Понятие естеств. модуляции распространяют также на волны. Так, напр., волновой пучок достаточной интенсивности может изменять параметры среды и, как следствие, модулировать свою плотность (см. Самофо-кисировка света). При распространении волн в нелинейных диспергирующих средах (жидкостях, плазме) возникает явление автомодуляции волн, связанное с разл. видами неустойчивости волн по отношению к НЧ-пространственно-временным возмущениям. Естеств модуляция находит практич. приложение в радио- и оптич. спектроскопии для диагностики параметров разнообразных сред; в нелинейной оптике для формирования мощных световых потоков; в акустике и др областях прикладной физики. Способы практич. реализации M. к. связаны, как правило, с нелинейными устройствами, параметры к-рых (в радиотехнике, напр., это ёмкость, сопротивление; в акустике — плотность, и т. п. ) можно изменять во времени в соответствии с законом модуляции. Техн. устройства, реализующие M. к., наз. модуляторами.
Лит.: Pытов С. M., Модулированные колебания и вол-ны, «Тр. ФИАН», 1940, т. 2, в. 1; Fренкс Л., Теория сигна-лов, пер. с англ. M., 1974; Баскаков С. И., Радиотехниче-ские цепи и сигналы, M., 1983; Вайнштейн Л. А., Вак-ман Д. E., Разделение частот в теории колебаний и волн, M., 1983. Ю. К. Богатырёв, M. А. Миллер.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .
Источник
