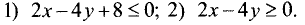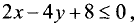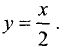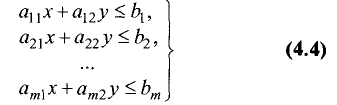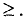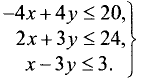Что значит множество точек

Урок алгебры в 7-м классе по теме «Множества точек на координатной плоскости»

Разделы: Математика

Цели урока:

• формирование умения перейти от алгебраического описания множества точек к геометрическому изображению и наоборот;
• продолжить формирование умений, связанных с работой на координатной плоскости;
• формирование умения мыслить по аналогии, умения наблюдать и делать выводы, умения обобщать.

I. Оргмомент

II. Актуализация знаний

1. Определить координаты точек.

2. Построить отрезок LE, если L(–1; 2), Е(4; 5).
Построить прямую РТ, если Р(0; 3), Т(–1; –2)

III. Постановка проблемы

Приготовить пять координатных плоскостей.
Отметьте указанные точки на координатных плоскостях
1) А(3; 1), В(4; –1), С(–5; –2).

2) М(3; –2), N(–4; –2), К(1.5; –2)

3) Р(5; –1), Е(5; 4), F(5;1/2)

4) Х(6; 0), У(–3; 0), Z(1; 0)

5) Q(0; 3), N(0; 5), L(0; –1/2)

Посмотрите на чертежи, что можно сказать о расположении точек:
В первом случае?

В остальных случаях?
Что общего?

Мы выяснили, что общее в 2–4 рисунках то, что точки лежат на одной прямой.

IV. «Открытие» детьми нового знания

Подумайте, как можно записать множество точек, изображенных на рисунке

Какое условие является общим для этих точек?

А как это условие записать на языке алгебры? у = 3
(ордината равна 3)
На рис.2 проведите через отмеченные точки у = – 2
прямую, запишите множество этих точек.
Проведите на остальных рисунках через отмеченные точки прямые.
А как бы вы записали на языке алгебры множества точек, изображенных на рисунке 3? 4? 5?
Подумайте, а затем проверим правильность записей.

Что означают эти записи на математическом языке?

Множество точек расположенных где? На координатной плоскости

Итак, тема нашего урока:

А цель урока?
Учитель еще раз формулирует тему и цель урока, записывает тему на доске.
Изобразите на координатной плоскости множество точек, удовлетворяющих условию:

У обучающихся На доске

х = 5
х = – 4

у = – 4
у = 1

Проверяем правильность построения и записи.
А теперь давайте попробуем изобразить множество точек, удовлетворяющих условию х > 3.
Как можно это условие прочитать на русском языке? – точки, большие 3

Чтобы построить точку в координатной плоскости, необходимо, что знать?

Прочитайте условие х > 3

Построим в координатной плоскости прямую х = 3

Где будут располагаться точки, абсцисса которых больше 3?

Покажите несколько таких точек

А множество всех точек удовлетворяющих условию х > 3 можно показать с помощью штриховки

х > 3 задает полуплоскость, расположенную правее прямой х = 3 и все точки этой прямой.

Изобразите множество точек, удовлетворяющих условию у 1.

Проверяем правильность построения.
Постройте множество точек у > 1.
Каким свойством обладают точки этого множества у них ордината больше 1
А как они должны располагаться относительно – выше
прямой у = 1
А точки прямой у = 1 удовлетворяют условию y > 1 нет
А как это показать? – не знаем

В этом случае прямая у = 1 изображается пунктиром.

Изобразим множество точек, удовлетворяющих условию у > 1.

Приглашается ученик к доске.

Изобразите множество точек, удовлетворяющих условию:

Выделите множество точек, удовлетворяющих одновременно всем этим условиям.
Какую фигуру получили?

VI. Самостоятельная работа с последующей самопроверкой

1. Опишите на алгебраическом языке множества точек, изображенные на рисунках.

1.

2. Изобразите на координатной плоскости множества точек, удовлетворяющих условию:

Источник

Множество точек. Изображение некоторых множеств точек на плоскости.

Представим на координатной плоскости множество точек, удовлетворяющих условию х = 5 и х = -4,

В первом случае прямые параллельны оси ординат, во втором – абсцисс.

На прямой может быть расположено неограниченное количество точек. И у всего этого множества точек, координаты удовлетворяют условиям х = 5 и х = -4; у = -4 и у = 1.

На координатной прямой неравенству х 3. Проанализируем, что это за точки:

— множество точек, абсцисса которых больше или равна 3

— точки, лежащие правее прямой х = 3 и на прямой.

Алгоритм построения будет иметь вид:

— строим в координатной плоскости прямую: х = 3;

— определяем, где будут находиться точки, абсцисса которых больше 3; ответ – правее;

— множество всех точек удовлетворяющих условию х > 3 покажем при помощи штриховки;

х > 3 задает полуплоскость, находящаяся правее прямой х = 3 и все точки этой прямой. Прямую изображаем одной цельной линией, этим указываем, что все точки расположенные на прямой так же включены во множество.

Представим множество точек, удовлетворяющих условию у 1.

Постройте множество точек у > 1. По аналогии, точкам этого множества присуще свойство — у них ордината больше 1.

Следовательно, они будут находиться выше прямой у = 1. В соответствии со знаком неравенства точки прямой у = 1 не удовлетворяют условию y > 1. Графически мы это покажем, изобразив прямую у = 1 пунктиром.

Представим множество точек, соответствующих условию у > 1 так:

Представим на координатной плоскости множества точек, соответствующих условию: -2 ≤ х ≤ 2.

Источник

Выпуклые множества точек и их свойства с примерами решения и образцами выполнения

Основные определения:

Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.

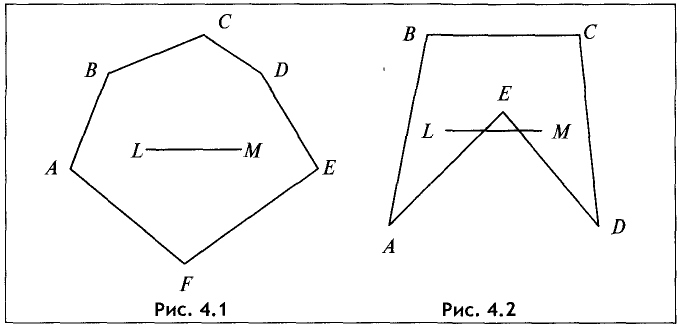
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.

Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.

Пересечение любого числа выпуклых множеств есть выпуклое
множество.

Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.

Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.

Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.

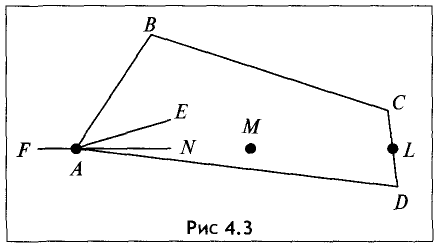
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.

Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.

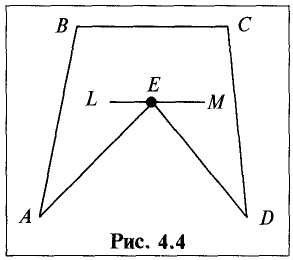
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).

Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.

Множество точек называется замкнутым, если оно включает все свои граничные точки.

Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.

Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.

Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.

Геометрический смысл решений неравенств

Рассмотрим решения неравенств с двумя переменными типа

Теорема:

Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой

включая и эту прямую, а другая полуплоскость — множеством решений неравенства

Пример:

Построить график множества решений следующих
неравенств:

Решение:

В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.

1.Границей первой полуплоскости является прямая

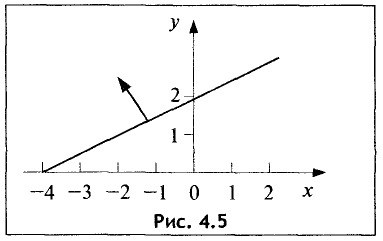
Представим уравнение этой прямой в виде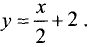
Ее график представлен на рис. 4.5.

Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство

видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.

2.Границей второй полуплоскости является прямая

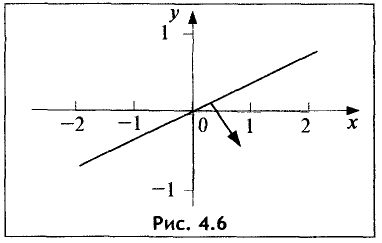
Представим это уравнение в виде

График исследуемой прямой представлен на рис. 4.6.

В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 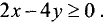Так как неравенство выполняется (4 > 0), то искомой является нижняя полуплоскость. ►

Основные свойства выпуклого множества точек

Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.

Теорема:

Множество решений совместной системы т линейных
неравенств с двумя переменными

является выпуклым многоугольником (или выпуклой многоугольной областью).

Знаки некоторых или всех неравенств могут быть

Эту теорему для n переменных можно сформулировать
следующим образом.

Теорема:

Множество решений совместной системы m линейных
неравенств с n переменными

является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.

Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.

Область решений системы, удовлетворяющая условиям неотрицательности 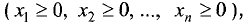называется областью неотрицательных (или допустимых) решений.

Пример:

Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:

Решение:

Областью решений является треугольник ABC, представленный на рис. 4.7.

Сторона АВ треугольника, образованная границей первого неравенства системы, определяется уравнением прямой у = х + 5 .

Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 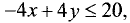видим, что оно выполняется, так как 0

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник