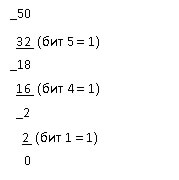- Нумерация бит — Bit numbering
- СОДЕРЖАНИЕ
- Наименее значимый бит
- Наименьший бит в цифровой стеганографии
- Наименьший байт
- Старший бит
- Старший байт
- Пример беззнакового целого числа
- Сначала старший и младший бит
- Нумерация битов LSB 0
- Нумерация битов MSB 0
- Другой
- использование
- Что значит младший бит
- 1.1 Двоичные числа
- Наименее значащий бит
- Резюме
- Оцифрованный сигнал
- Паритет
Нумерация бит — Bit numbering
В вычислении , немного нумерации является соглашением , используемым для определения битовых позиций в двоичном числе или контейнере такого значения. Номер бита начинается с нуля и увеличивается на единицу для каждой последующей битовой позиции.
СОДЕРЖАНИЕ
Наименее значимый бит
В вычислении , то младший значащий бит ( LSB ) является бит положение в двоичном целое число дает значение единицы, то есть определить , является ли число четным или нечетным. LSB иногда называют битом младшего разряда или крайним правым битом из-за принятого в позиционном обозначении правила записи менее значимых цифр дальше вправо. Она аналогична значащая цифра в виде десятичного целого числа, которое является цифрой в них (самом правом) положении.
Обычно каждому биту присваивается номер позиции в диапазоне от нуля до N-1, где N — количество битов в используемом двоичном представлении. Обычно номер бита — это просто показатель степени для соответствующего веса бита в базе 2 (например, в 2 31 ..2 0 ). Некоторые производители ЦП присвоили номера битов противоположным образом (что не то же самое, что и другой порядок следования байтов ). В любом случае, самый младший бит остается однозначным как единичный бит.
Наименее значимые биты (множественное число) — это биты числа, ближайшего к младшему разряду и включающего его. Младшие значащие биты обладают полезным свойством быстро изменяться, если число изменяется даже незначительно. Например, если 1 (двоичный 00000001) добавить к 3 (двоичный 00000011), результатом будет 4 (двоичный 00000100), а три младших бита изменятся (с 011 на 100). Напротив, три старших бита (MSB) остаются неизменными (от 000 до 000). Из-за этой изменчивости наименее значимые биты часто используются в генераторах псевдослучайных чисел , стеганографических инструментах, хэш-функциях и контрольных суммах .
Наименьший бит в цифровой стеганографии
В цифровой стеганографии конфиденциальные сообщения можно скрыть, манипулируя и сохраняя информацию в наименее значимых битах изображения или звукового файла. Пользователь может позже восстановить эту информацию, извлекая младшие биты обработанных пикселей, чтобы восстановить исходное сообщение. Это позволяет скрывать хранение или передачу цифровой информации.
Наименьший байт
LSB также может означать наименее значимый байт . Значение аналогично значению битов: именно байт в многобайтовом числе имеет наименьшее потенциальное значение.
Старший бит
В вычислениях , то самый старший бит ( MSB ) является битым положением в двоичном числе , имеющее наибольшее значение. MSB иногда называют старшим битом или крайним левым битом из-за соглашения в позиционной записи о записи более значимых цифр дальше влево.
Знаковый бит является MSB в двоичном числа . В обозначениях дополнения до единицы и двух «1» означает отрицательное число, а «0» означает положительное число.
Обычно каждому биту присваивается номер позиции в диапазоне от нуля до N-1, где N — количество битов в используемом двоичном представлении. Обычно назначенный номер бита — это просто показатель степени для соответствующего веса бита в основании 2 (например, в ). Некоторые производители ЦП назначают номера битов по-разному. Вне зависимости от нумерации, то MSB остается наиболее значащий бит. 2 31 ..2 0
Старший байт
MSB также может обозначать самый старший байт . Значение байтов аналогично значению битов: это байт многобайтового числа, который имеет наибольшее потенциальное значение.
Чтобы избежать двусмысленности между битом и байтом, часто используются менее сокращенные термины MSbit или MSbyte .
Пример беззнакового целого числа
Эта таблица иллюстрирует пример десятичного значения 149 и расположение LSB. В этом конкретном примере позиция значения единицы (десятичная 1 или 0) находится в позиции бита 0 (n = 0). MSB обозначает наиболее значимый бит , а LSB обозначает наименее значимый бит .
| Двоичный (десятичный: 149) | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| Битовый вес для данной битовой позиции n (2 n ) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Метка битовой позиции | MSB | LSB |
Положение LSB не зависит от того, в каком порядке передаются или сохраняются биты, что является вопросом порядка байтов .
Сначала старший и младший бит
Выражения « старший значащий бит — первый» и « младший значащий бит», наконец , указывают на порядок следования битов в байтах, отправляемых по сети в протоколе последовательной передачи или в потоке (например, аудиопотоке).
Большинство значащего бита означает , что самый значимый бит будет прибывающим первым: следовательно , например, шестнадцатеричное число 0x12 , 00010010 в двоичном представлении, поступят в виде последовательности 0 0 0 1 0 0 1 0 .
Первый младший бит означает, что младший бит прибудет первым: следовательно, например, то же шестнадцатеричное число 0x12 , опять же 00010010 в двоичном представлении, прибудет как (обратная) последовательность 0 1 0 0 1 0 0 0 .
Нумерация битов LSB 0
Когда нумерация битов начинается с нуля для младшего значащего бита (LSB), схема нумерации называется «LSB 0». Этот метод нумерации битов имеет то преимущество, что для любого числа без знака значение числа может быть вычислено с использованием возведения в степень с числом битов и основанием 2. Таким образом, значение двоичного целого числа без знака равно
∑ я знак равно 0 N — 1 б я ⋅ 2 я <\ Displaystyle \ сумма _ <я = 0>^
где b i обозначает значение бита с номером i , а N обозначает общее количество битов.
Нумерация битов MSB 0
Точно так же, когда нумерация битов начинается с нуля для самого старшего бита (MSB), схема нумерации называется «MSB 0».
Таким образом, значение двоичного целого числа без знака равно
∑ я знак равно 0 N — 1 б я ⋅ 2 N — 1 — я <\ Displaystyle \ сумма _ <я = 0>^
Другой
Algol 68 «сек эля оператор эффективен„старший бит 1 битой нумерация“ , как биты пронумерованы слева направо, причем первый бит (биты Эль 1) быть„самым старшим бит“, и выражение (биты эль биты ширина) давая «младший значащий бит». Точно так же, когда биты приводятся (приведение типов) к массиву логических значений ([] bool bits), первый элемент этого массива (биты [ lwb биты]) снова является « старшим значащим битом».
Для нумерации MSB 1 значение двоичного целого числа без знака равно
∑ я знак равно 1 N б я ⋅ 2 N — я <\ displaystyle \ sum _ <я = 1>^
PL / I нумерует BIT- строки, начиная с 1 для крайнего левого бита.
Функция Fortran BTEST использует нумерацию LSB 0.
использование
Процессоры с прямым порядком байтов обычно используют нумерацию битов «LSB 0», однако оба соглашения о нумерации битов можно увидеть в машинах с прямым порядком байтов . Некоторые архитектуры, такие как SPARC и Motorola 68000, используют нумерацию битов «LSB 0», в то время как S / 390 , PowerPC и PA-RISC используют «MSB 0».
Рекомендуемый стиль для документов запроса комментариев (RfC) — это нумерация битов «MSB 0».
Нумерация битов обычно прозрачна для программного обеспечения , но некоторые языки программирования, такие как Ada, и языки описания оборудования, такие как VHDL и verilog, позволяют указать соответствующий порядок битов для представления типа данных.
Источник
Что значит младший бит
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
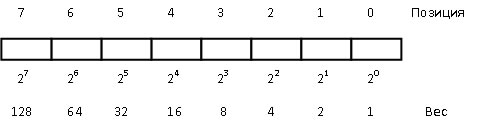
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Прежде всего, вычтите из десятичного числа наибольший возможный двоичный вес и запишите 1 в эту позицию бита. Затем из результата вычтите новый наибольший возможный двоичный вес и запишите 1 в эту новую позицию бита. Так — до получения нулевого результата. Например, преобразование числа 50 в двоичное:
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
Оперативная память ЭВМ состоит из блоков памяти по 1024 байта. Число 1024 есть 2 10 . Число 1024 имеет стандартное обозначение К. Следовательно, ЭВМ, имеющая 48 К памяти, содержит 48 x 1024 = 49152 байта.
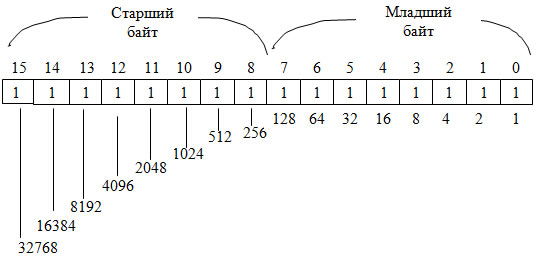
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
11110001 241 (10)
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
Если слово (байт) содержит число со знаком, то в старшем бите содержится знак (0 есть +, 1 есть -), а оставшиеся 15 или 7 битов содержат само число в дополнительном коде. Дополнительный код положительного числа совпадает с записью такого же числа без знака. Для получения дополнительного кода отрицательного числа из его абсолютного значения используется следующее правило:
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Вычитание двух положительных чисел заменяется суммированием первого числа с дополнением второго. Таким образом, как суммирование, так и вычитание выполняет одно и то же аппаратное устройство – сумматор. Кроме этого свойства использование дополнения имеет еще одно достоинство — число ноль имеет единственное представление, т.е. нет двух нулей – положительного и отрицательного. Приведем целые числа в окрестностях 0:
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.
Источник
Наименее значащий бит
Наименее значимый бит (на английском языке, наименее значащий бит или младший бит ) является бит в течение битовой карты данных , имеющих наименьший вес или положение (право в позиционной системы счисления обычно). Иногда его также называют LSD для наименьшей значащей цифры.
Например, для одного числа в обычном двоичном представлении младший бит является крайним правым битом: 0101011 0 .
Напротив, есть самый старший бит (MSB для старшего значащего бита), иногда также называемый MSD для старшего значащего разряда.
Обратите внимание, что иногда делается различие между lsb (LSB, записанным в нижнем регистре) для наименее значимого бита и LSB (в верхнем регистре) для наименее значимого байта английского языка , который затем обозначает наименее значимый байт ( байт ) в числе, состоящем из нескольких байтов. (один байт состоит из 8 бит). Соответственно для msb и MSB.
Резюме
Оцифрованный сигнал
Во время квантования , шага оцифровки , младший значащий бит соответствует наименьшему изменению электрического напряжения, на котором сигнал может быть дискретизирован, шагу дискретизации . Поэтому LSB используется как единица измерения таких величин, как линейность оцифровки или вносимые ею искажения . В идеале искажение должно составлять 1 младший бит: тогда разница между реальным и дискретным уровнями будет шагом дискретизации.
Паритет
Мы можем быстро узнать четность двоичного числа, записанного в естественном двоичном коде, посмотрев на младший бит: если он равен 1, число нечетное; если 0, то число четное. Это возможно, потому что младший бит — единственный бит, который по построению «добавляет» нечетное число к двоичному числу: 1 .
Источник