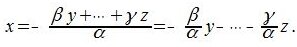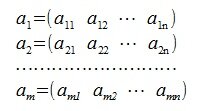Что значит линейно независимый вектор

Линейная зависимость и линейная независимость векторов

Векторы x, y, . z называются линейно зависимыми векторами, если существуют числа α, β, . γ, из которых хотя бы одно отлично от нуля, такие что справедливо равенство:

Другими словами линейная зависимость группы векторов означает, что существует среди них вектор, который можно представить линейной комбинацией других векторов этой группы.

Допустим 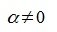. Тогда

Следовательно вектор x линейно зависим из векторов этой группы.

Векторы x, y, . z называются линейно независимыми векторами, если из равенства (0) следует, что

То есть группы векторов линейно независимы, если ни один вектор не может быть представлен линейной комбинацией других векторов этой группы.

Определение линейной зависимости векторов

Пусть заданы m векторов строк порядка n:

Составим матрицу из этих векторов и добавим с правой стороны столбец, в котором запишем индексы соответствующих строк:

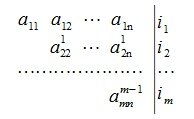
Сделав Гауссово исключение, приведем матрицу (2) к верхнему треугольному виду. Элементы последнего столбца изменяются только тогда, когда строки переставляются. После m шагов исключения получим:

где i₁, i₂, . i_m — индексы строк, полученные при возможной перестановки строк. Рассматривая полученные строки из индексов строк исключаем те, которые соответствуют нулевым вектором строк. Оставшиеся строки образуют линейно независимые векторы. Отметим, что при составлении матрицы (2) изменяя последовательность векторов строк, можно получить другую группу линейно независимых векторов. Но подпространство, которую оба эти группы векторов образуют совпадают.

Определение линейной зависимости векторов онлайн

Для определения линейной зависимости векторов используйте матричный онлайн калькулятор .

Источник

Что значит линейно независимый вектор

Определение 1. Система векторов 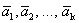называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой — в противном случае.

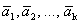
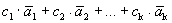
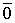
Определение 1´. Система векторов называется линейно зависимой, если найдутся числа с ₁ , с ₂ , …, с _k , не все равные нулю, такие, что линейная комбинация векторов с данными коэффициентами равна нулевому вектору: = , в противном случае система называется линейно независимой.

Покажем, что эти определения эквивалентны.

Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:

,

.

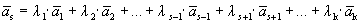
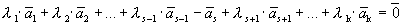
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.

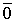
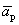
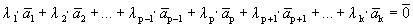
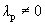
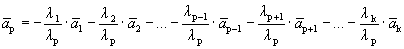
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна , причем не все коэффициенты комбинации равны нулю, например, коэффициенты при векторе .

,

,

.

Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.

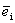
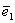
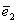
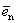
Определение 2. Единичным вектором, или ортом, называется n -мерный вектор , у которого i -я координата равна единице, а остальные — нулевые.

. (1, 0, 0, …, 0),

(0, 1, 0, …, 0),

(0, 0, 0, …, 1).

Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.

Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.

= .

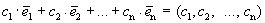
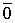
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.

Каждый вектор n -мерного пространства ā(а ₁ , а ₂ , . а _n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора

.

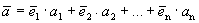
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.

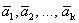
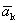
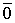
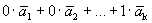
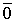
Доказательство. Пусть дана система векторов и один из векторов является нулевым, например = . Тогда с векторами данной системы можно составить линейную комбинацию, равную нулевому вектору, причем не все коэффициенты будут нулевыми:

= .

Следовательно, система линейно зависима.

Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

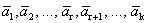
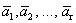
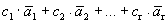
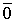
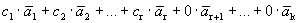
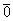
Доказательство. Дана система векторов . Предположим, что система линейно зависима, т.е. найдутся числа с ₁ , с ₂ , …, с _r , не все равные нулю, такие, что = . Тогда

= .

Получилось, что линейная комбинация векторов всей системы равна 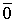, причем не все коэффициенты этой комбинации равны нулю. Следовательно, система векторов линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.

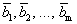
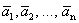
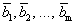
Теорема 4 (теорема Штейница). Если каждый из векторов является линейной комбинацией векторов и m > n , то система векторов линейно зависима.

Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.

Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.

Источник

Линейно зависимые и линейно независимые вектора.

Определение. Линейной комбинацией векторов a ₁, . a_n с коэффициентами x ₁, . x_n называется вектор

Свойства линейно зависимых векторов:

Примеры задач на линейную зависимость и линейную независимость векторов:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

	x 1 + x 2 = 0
	x 1 + 2 x 2 — x 3 = 0
	x 1 + x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 1 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 1 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 1 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 1 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 0 0

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x ₁, x ₂, x ₃ таких, что линейная комбинация векторов a , b , c равна нулевому вектору, например:

а это значит вектора a , b , c линейно зависимы.

Ответ: вектора a , b , c линейно зависимы.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

	x 1 + x 2 = 0
	x 1 + 2 x 2 — x 3 = 0
	x 1 + 2 x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 2 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 2 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 2 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 2 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 1 0

из первой строки вычтем третью; к второй строке добавим третью:

1 — 0 0 — 0 1 — 1 0 — 0 0 + 0 1 + 0 -1 + 1 0 + 0 0 0 1 0

1 0 1 0 0 1 0 0 0 0 1 0

Данное решение показывает, что система имеет единственное решение x ₁ = 0, x ₂ = 0, x ₃ = 0, а это значит вектора a , b , c линейно независимые.

Ответ: вектора a , b , c линейно независимые.

Источник