- Что значит линейная часть приращения функции
- Что такое дифференциал функции?
- Производная как смысл жизни или что такое дифференциал(d)
- Пролог:
- Начало
- Смотрим дифференциалу в лицо
- Вернемся к равенству
- Немного пределов
- Дифференциал функции в математике с примерами решения и образцами выполнения
- Геометрический смысл дифференциала
- Вычисление дифференциала
- Дифференциалы высших порядков
- Приложение дифференциала приближенным вычислениям
- Вычисление приближенного значения приращения функции
- Вычисление приближенного числового значения функции
- Приближенное вычисление степеней
- Приближенное извлечение корней
- Дополнение к дифференциалу
- Понятие о дифференциале в высшей математике
- Сравнение бесконечно малых величин между собой
- Геометрическое изображение дифференциала
- Дифференциал второго порядка
- Приложение дифференциала к приближенным вычислениям
- Кривизна кривой
- Кривизна окружности
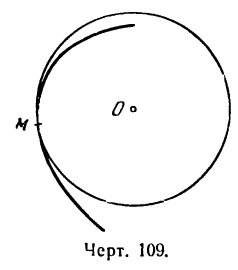
- Радиус кривизны кривой
- Как найти дифференциал — подробная инструкция
- Бесконечно малые величины
- Дифференциал
- Таблица дифференциал
- Применение к приближенным вычислениям
- Дифференциал площади криволинейной трапеции
- Применение дифференциала к различным задачам
Что значит линейная часть приращения функции
| Дифференциал функции и вариация функционала |   |
Приращение аргумента (или дифференциал аргумента) есть произвольное изменение Δx = dx переменной x в пределах области определения функции f . Приращение функции f прелставляет собой ее изменение Δf , обусловленное приращением аргумента. В случае функции одной переменной Дифференциал функции есть главная линейная часть ее приращения относительно дифференциалов аргументов. В частности, дифференциал функции f одной переменной x имеет вид Важно отметить, что чисто формально дифференциал функции f (x) можно определить уравнением Пусть функционал
Приращение функционала
Аналогом дифференциала функции f (x) является вариация функционала
Заметим, что не всегда можно выделить главную линейную часть Источник Что такое дифференциал функции?Понятие дифференциала функции связано с такими важными математическими разделами как дифференциальное и интегральное исчисление и тесно связано с понятием производной функции. Наиболее часто дифференциал применяется для приближенных вычислений, а также для оценки погрешностей формул и измерений. Дифференциал функции — это линейная часть приращения функции. Говоря о значении дифференциала функции, рассматривают конкретную точку функции и бесконечно малое изменение аргумента. Пусть xo есть некоторая точка из области определения функции f(x), а Δx — есть бесконечно малая величина. Тогда дифференциал функции находится как произведение значения производной функции и приращения её аргумента. Дифференциал функции f(x) обозначается как df(x). История открытия дифференциала Чаще всего открытие дифференциально-интегрального исчисления принято связывать с именем Исаака Ньютона, однако, этот факт активно оспаривают учёные со всего света. Действительно, открытие целого нового направления в науке, столь значимого для её развития, было бы ошибочно считать заслугой только одного учёного. Изначально интегрирование связывали с вычислением площадей и объёмов криволинейных фигур. Такие задачи, как известно, решались ещё во времена Архимеда, поэтому его имя также имеет отношение к открытию дифференциального исчисления. Также дифференцирование имеет отношение к решению задач на проведение касательных к различным кривым. Данное направление активно развивали греческие математики. В те времена математики столкнулись с трудностью, которую не смогли решить в дальнейшем и представители Нового времени. Дело в том, что для определения направления прямой требовалось знать координаты как минимум двух точек, а касательная имеет лишь одну точку соприкосновения с кривой. Этот факт натолкнул учёных на мысль о том, что в одной точке кривая может иметь несколько касательных. В то время ученые пришли к выводу, что прямая состоит не из точек, а из отрезков минимальной длины. Таким образом, они считали направление касательной в некоторой точке совпадающим с направлением атомарного отрезка в данной точке. В дальнейшем учёные Нового времени опровергли данную теорию. В этот период огромный вклад в развитие науки внёс Исаак Ньютон. Ученый сформулировал определения и принципы решения производных, а также основы дифференциального исчисления, которых придерживаются учёные и в наши дни. Дифференциальное исчисление широко применяется в математике и других науках для решения различных задач. Геометрический смысл дифференциала Геометрический смысл дифференциала заключается в следующем: дифференциал функции f(x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x,y) при изменении координаты x на величину Δх=dx. Дифференциал является главной линейной частью функции относительно приращения аргумента. Чем меньше приращение функции, тем большая доля приращения приходится на эту линейную часть. Таким образом, при бесконечно малом Δх, приращение функции можно считать равным ее дифференциалу. Это свойство дифференциала позволяет использовать его для приблизительных вычислений и оценки погрешностей измерений. Применение дифференциала в приближенных вычислениях Поскольку дифференциал функции является частью ее приращения, то при бесконечно малом приращении аргумента он приблизительно равен приращению функции. При этом чем меньше приращение аргумента, тем точнее значение функции. Этот факт даёт возможность использования дифференциалов для приближённых вычислений. С помощью таких вычислений можно решать различные виды задач. Приближённые вычисления практически всегда связаны с наличием погрешности. Использование дифференциала для оценки погрешностей Результаты измерений в большинстве случаев содержат ошибку, обусловленную неточностью измерительных приборов. Число, несколько превышающее или равное этой неточности, называется «предельной абсолютной погрешностью». Отношение предельной погрешности к значению измеряемой величины называют «предельной относительной погрешностью». Для оценки величины погрешностей измерений используют дифференциальное исчисление. Источник Производная как смысл жизни или что такое дифференциал(d)Пролог:Эта одна из статей серии «Производная как смысл жизни», сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему. НачалоДля начала лучше ознакомиться со статьей о самой прозводной (скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше. Как мы уже знаем формула записи производной выглядит так: -напоминаю, что Δx — приращение аргумента, Δy — приращение функции. Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю «неточность». Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение «неточности»(в статье о производной об этом подробнее рассказано). Теперь выразим из этого равенства приращение функции(Δy): И на этом следует пока остановиться и рассмотреть график. Смотрим дифференциалу в лицоРасмотрим такой график: Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена. Как мы видим приращение функции(Δy) как бы разделено на две части: BC и CD. Дифференциал(d) — это линейная часть приращения функции. Зная это введем обозначение на графике: Вернемся к равенствуBD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx. Из формулы мы понимаем, что dy=f'(x)Δx. Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента). Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx. Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx. Немного пределовДобавим с левой части и с правой предел В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит: Зная, что f'(x)Δx = dy, мы делаем вывод, что: Тогда так же мы можем сказать, что дифференциал функции — это приращения функции у которой приращение аргумента стремиться к нулю, ну и это следуется из того же графика. Источник Дифференциал функции в математике с примерами решения и образцами выполненияПонятие дифференциала функции: Известно, что если функция где функция Слагаемое Определение: Дифференциалом функции Дифференциал функции обозначается Пример: Найти дифференциал функции Решение: По формуле (3) имеем: Итак, дифференциал Пример: Найти дифференциал сложной функции Решение: По формуле (4) находим: Но — Таким образом, форма дифференциала не зависит от того, является аргумент данной функции независимой переменной или функцией другого аргумента. Это свойство дифференциала сложной функции называется инвариантностью формы дифференциала. Пример: Найти дифференциал функции Решение: По формуле (4) находим: Геометрический смысл дифференциалаПусть Из прямоугольного треугольника Таким образом, дифференциал функции Можно показать, что этот вывод не зависит от расположения графика функции и касательной на координатной плоскости. Дифференциал может быть как меньше приращения функции (см. рис. 74), так и больше (рис. 75). Однако при достаточно малых приращениях принять Вычисление дифференциалаМы установили, что дифференциал функции т. е. дифференциал функции По формуле (1) можно вычислить дифференциал любой дифференцируемой функции. Так, например; Аналогично, каждой из основных формул дифференцирования можно сопоставить соответствующую формулу для вычисления дифференциала. Пример: Найти дифференциал функции Решение: По формуле (1) находим: Пример: Найти дифференциал функции Решение: Находим: Дифференциалы высших порядковИз формулы Рассмотрим дифференциал Дифференциал от дифференциала функции Таким образом, Аналогично определяются дифференциалы третьего порядка: Вообще, дифференциалом п-го порядка называется дифференциал от дифференциала Таким образом, для нахождения дифференциала п—го порядка функции Пример: Найти дифференциалы первого, второго и третьего порядка функции Решение: Находим соответствующие производные Приложение дифференциала приближенным вычислениямРассмотрим функцию Выше (§ 2) было установлено, что при достаточно малых Так как вычислять Вычисление приближенного значения приращения функцииПример: Найти приближенное значение приращения функции Решение: Применив формулу (3), получим: Посмотрим, какую погрешность мы допустили, вычислив дифференциал данной функции вместо ее приращения. Для этого найдем истинное значение приращения: Далее, находим абсолютную погрешность приближения: а затем и относительную погрешность: Погрешность приближения оказалась довольно малой, что еще раз подтверждает целесообразность применения формулы (3). Вычисление приближенного числового значения функцииИз формулы (1) имеем Пример: Найти приближенное значение функции Решение: Представим Приближенное вычисление степенейРассмотрим функцию По этой формуле наводят приближенное значение степеней. Пример: Найти приближенное значение степени Решение: Представим данную степень в виде Приближенное извлечение корнейПри Формула (6), известная и по школьному курсу, дает возможность найти приближенные значения различных корней. Пример: Найти приближенное значение корня Решение: Представим данный корень в виде Дополнение к дифференциалу
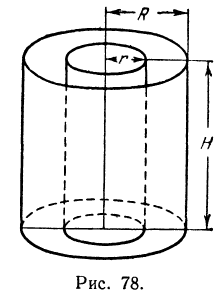
Понятие о дифференциале в высшей математикеСравнение бесконечно малых величин между собойI. Мы рассмотрели действия над бесконечно малыми величинами и показали, что в результате сложения, вычитания и умножения их получаются также бесконечно малые величины. Однако частное от деления двух бесконечно малых друг на друга может быть не только бесконечно малой величиной, но и бесконечно большой и конечной. В самом деле, пусть, например, а — бесконечно малая, тогда 1) отношение 2) отношение 3) отношение Первое отношение показывает, что бесконечно малая Второе отношение указывает на то, что а, неограниченно уменьшаясь, остается значительно больше, чем Сказанное можно иллюстрировать следующей таблицей: Принято бесконечно малую Что касается третьего отношения, то из него следует, что бесконечно малые 2а и а стремятся к нулю с одинаковой скоростью, так как при их изменении отношение Таким образом, частное от деления двух бесконечно малых величин позволяет сравнивать их между собой. Это сравнение особенно полезно в приближенных вычислениях, где отбрасывание бесконечно малых высшего порядка приводит к значительному упрощению вычислений. II. Возьмем функцию Множитель при Сравним изменение величины обоих слагаемых правой части равенства (I) с уменьшением х = 2 и, следовательно, у’ = 4, составим следующую таблицу значений этих слагаемых: Как видно из таблицы, слагаемые у’ Покажем, что то же самое справедливо для любой дифференцируемой функции f(x). Пусть дана функция у = f(х). Ее производная Согласно определению предела переменной имеем: где а—бесконечно малая величина при И здесь при уменьшении малая величина при Определение: Главная часть у’ Дифференциал функции у = f(х) принято обозначать символом dу. Таким образом Дифференциал аргумента dх принимают равным приращению аргумента Поэтому равенство (3) можно переписать в следующем виде: т. е. дифференциал функции равен произведению производной функции на дифференциал аргумента. Из формулы (4) следует: Равенство (5) показывает, что производная функции есть отношение дифференциала функции к дифференциалу аргумента. На этом основании производную функции часто выражают в виде III. Заменив в равенстве (2) Как было показано выше, В практических вопросах часто используют формулу (7), т. е. берут дифференциал функции вместо ее приращения, делая при этом незначительную ошибку и тем меньшую, чем меньше Примечание: В случае линейной функции Множитель Итак, в случае линейной функции Геометрическое изображение дифференциалаВозьмем функцию у = f(x), график которой изображен на рис. 104. Пусть абсцисса точки М тогда ордината ее Дадим аргументу х приращение Проведем в точке М касательную к кривой; полученный при этом отрезок QN, равный приращению ординаты точки М, движущейся по касательной, называется приращением ординаты касательной. Из прямоугольного треугольника МQN имеем: а, согласно геометрическому смыслу производной, Таким образом, если в точке М кривой у = f(х) провести касательную, то дифференциал функции у = f(х) в этой точке изобразится приращением ординаты касательной, соответствующим приращению ее абсциссы на dx. Дифференциал функции в данной точке может быть как меньше приращения ее (рис. 104), так и больше (рис. 105). Дифференциал второго порядкаДифференциал dy функции у = f(x), называемый первым дифференциалом или дифференциалом первого порядка, представляет собой также функцию x, а потому и от него можно найти дифференциал, который называют вторым дифференциалом или дифференциалом второго порядка. В этом случае пишут d(dy) или короче Найдем выражение дифференциала второго порядка от функции через ее производную. Для этого продифференцируем по х равенство. считая dx постоянным множителем (так как dx не зависит от х): Но согласно формуле (4) т. е. дифференциал второго порядка равен произведению второй производной функции на квадрат дифференциала аргумента. Из равенства (1) следует Это дает основание для выражения второй производной функции в виде отношения Приложение дифференциала к приближенным вычислениямРассмотрим несколько примеров использования дифференциала в приближенных вычислениях. а) Определение приращения функции. Пример: Найти приближенно приращение функции при х = 2 и Решение: Так как приращение аргумента — величина малая, то согласно формуле (7) можем приращение функции заменить ее дифференциалом. Дифференциал же данной функции Заменив в равенстве (1) х и dх их значениями, получим: Посмотрим, какую ошибку мы делаем, беря дифференциал вместо приращения. Для этого найдем точное значение приращения функции: Сравнивая полученное точное значение Ошибка оказалась очень малой. Пример: Шар радиуса R = 20 см был нагрет, отчего радиус его удлинился на 0,01 см. Насколько увеличился при этом объем шара? Решение: Объем шара определяется по формуле Каждому значению R по закону, заданному этой формулой, отвечает одно определенное значение v, т. е. v есть функция от R. Следовательно, наша задача сводится к определению приращения функции v при заданном приращении аргумента R. Так как приращение аргумента мало то мы можем приращение функции заменить ее дифференциалом. Находим дифференциал функции v. б) Нахождение числового значения функции. Пусть требуется найти приближенное значение функции при x1 = 2,001, т. е. найти величину f(2,001). Представим х1 в виде суммы где 0,001 будем рассматривать как приращение аргумента. Из формулы для приращения функций Полагая Применив равенство (2) к данному примеру, можем написать: Равенство (2) может служить формулой для приближенного вычисления значения функции. в) Вычисление по приближенным формулам. Пользуясь формулой (2), выведем приближенные формулы для вычисления некоторых выражений. 1) Возьмем функцию и положим, что угол х, равный нулю, получает весьма малое приращение а. Применим формулу (2), полагая в ней х = 0 и dx = а. Получим: Отсюда следует, что синус очень малого угла приближенно равен самому углу; при этом нужно помнить, что угол должен быть выражен в радианной мере. Так, например, sin 0,003 2) Возьмем функцию Точно так же можно вывести равенство По формулам (3) и (4) можно быстро найти приближенную степень числа, близкого к единице; например: 3) Выведем формулу для приближенного вычисления выражения Но по формуле (3) Аналогично выводится формула По формулам (5) и (6) можно легко найти приближенное значение корня из числа, близкого к единице; например: Кривизна кривойПусть дана кривая, определяемая уравнением у = f(х) (рис. 106). Возьмем на ней две точки А и В и проведем в них касательные к кривой. При переходе от точки А к точке В касательная меняет угол наклона к положительному направлению оси абсцисс на некоторую величину. Если обозначим угол наклона касательной в точке А к оси Ох через а, то угол наклона касательной в точке В к той же оси, получив приращение Разделив Средняя кривизна кривой на разных ее участках может быть различной. Допустим теперь, что точка В, двигаясь по кривой, неограниченно приближается к точке А и Определение: Кривизной кривой в данной ее точке А называется предел, к которому стремится средняя кривизна дуги АВ при неограниченном приближении точки В к А. Согласно определению производной Преобразуем правую часть этого равенства, выразив dа. и ds через производные данной функции у =f(x). Согласно геометрическому смыслу производной имеем где а — угол наклона касательной к кривой у =f(х) в точке А к положительному направлению оси абсцисс (рис. 106); отсюда В этом равенстве аrctg у’ — функция от функции, так как аrctg у’ зависит от у’, a у’ зависит от х. Продифференцируем последнее равенство по аргументу х; получим: Найдем выражение ds через производную функции у =f(x). Для этого возьмем снова тот же участок АВ кривой (рис. 107). Будем рассматривать длину АВ как приращение дуги Разделив обе части равенства на Положим, что Применяя теоремы о пределе корня, суммы и степени , получим: поэтому равенство (3) примет вид Подставив значение da и ds в выражение (1), получим: Формула (5) позволяет найти кривизну кривой, определяемой уравнением у = f(x), в любой ее точке. Кривизна окружностиКривизну окружности можно определить по формуле (5) , но гораздо проще ее найти из следующих рассуждений. Проведем касательные в двух точках А и В окружности (рис. 108). Обозначив дугу АВ через на этом участке; она выразится дробью так как углы АО1В и Ясно, что такой же вывод мы получим, взяв другой какой-либо участок окружности. Следовательно, для любой точки окружности, т. е. кривизна окружности постоянна во всех ее точках и равна обратной величине ее радиуса. Радиус кривизны кривойПри изучении кривизны кривой подбирают такую окружность, кривизна которой равна кривизне кривой в той или иной ее точке. Центр этой окружнoсти называется центром кривизны кривой в соответствующей точке, радиус—радиусом кривизны кривой в этой точке, а сама окружность— окружностью кривизны (рис. 109). Определение: Окружностью кривизны в точке М кривой называется окружность, проходящая через точку М и имеющая с кривой одинаковую кривизну и общую касательную. Заметим, что центр окружности кривизны всегда располагается со стороны вогнутости кривой. Кривизна окружности, как мы знаем, Следовательно, и радиус кривизны кривой в точке ее определяется тем же равенством. Заменив К его значением, взятым из равенства (5) , получим формулу для определения радиуса кривизны кривой в любой ее точке: Применяя эту формулу к прямой линии, заданной, например уравнением так как Это значит, что прямую линию можно рассматривать как окружность бесконечно большого радиуса. Пример: Найти радиус кривизны кривой Решение: Найдем сначала первую и вторую производные функции Подставив значения у’ и у» в формулу (1), получим: Как найти дифференциал — подробная инструкцияБесконечно малые величиныБесконечно малые величины Определение: Бесконечно малой величиной вблизи h = a называется функция, зависящая от h и имеющая предел, равный нулю при условии, что независимое переменное стремится к а. Например, Бесконечно малые величины при условии, что независимое переменное стремится к нулю, будем называть «бесконечно малыми», не указывая, а только подразумевая условие Приведем примеры геометрического и физического содержания. Пример: Площадь S прямоугольника со сторонами х и h является бесконечно малой при любых х, так как Пример: Объема прямоугольного параллелепипеда, ребра которого равны 3, 2 и 2h, является бесконечно малым, так как Пример: Объем v прямоугольного параллелепипеда, ребра которого равны h, 2h и 5h, является бесконечно малым, так как Пример: По закону Ома v = Ri, где v — напряжение, R — сопротивление и i — ток. Отсюда следует, что при постоянном сопротивлении напряжение является бесконечно малым относительно тока, так как Пусть дана бесконечно малая величина а (h), т. е. Рассмотрим предел отношения Если этот предел существует и равен нулю, то бесконечно малая величина a (h) называется бесконечно малой более высокого порядка, чем h. Если предел равен конечному числу Пример: Пусть Пример: Пусть а(h) = sin 2h; а(h) — бесконечно малая того же порядка, что и h , поскольку Пример: а (h) = sin h —бесконечно малая, эквивалентная h , так как Пример: a( h ) = l — cos h . Так как то 1—cos h есть бесконечно малая более высокого порядка, чем h . В заключение параграфа рассмотрим функцию y = f(x). Пусть приращение независимого переменного равно А, тогда приращение функции равно Так как приращение h независимого переменного х не зависит от величины х, то для вычисления Пример: Пусть дана функция Если же x = 0 и по-прежнему h =1, то Здесь h сохраняет значение 1, но, поскольку х меняется, изменяется и Если же x = 2, а h = 0,5, то Здесь х сохраняет значение 2, но h меняется, поэтому меняется и Если f(х)—функция непрерывная, то, по определению, ее приращение ДифференциалПусть дана непрерывная функция у = f(х), имеющая производную. Тогда, по определению производной, Поэтому, если в правой части откинем знак предела, то получим ошибку, величина которой зависит и от x и от h. Обозначим эту ошибку через а( x , h ). Тогда вместо равенства (1) можно написать Про ошибку а( x , h ) мы знаем, что Это следует из равенства (1). Значит, ошибка а( x , h ) является бесконечно малой относительно приращения h независимого переменного. Если умножим обе части равенства (2) на h , то получим В левой части равенства (4) стоит приращение функции Очевидно, что первый член одного порядка с h , т. е. является линейным относительно h , а второй член а(x , h)h является бесконечно малой величиной более высокого порядка относительно h . Из равенства (4) получаем, что приращение функции с точностью до бесконечно малой высшего порядка равно f'(х)h ; это выражение называется дифференциалом функции. Определение. Дифференциал есть та часть при-ращения функции Дифференциал функции обозначают или dy, или df(x), так что Для симметрии записей вводится определение дифференциала независимого переменного. Определение: Дифференциалом независимого переменного называется его приращение. Дифференциал независимого переменного обозначается dx, так что имеем Операция нахождения дифференциала называется дифференцированием. Пример: Найдем дифференциал функции у = sin х. Так как (sin х)’ = cos х, то dy = dsin х = cos х • h = cos xdx. Пример: Вычислим значение дифференциала функции Подставляя сюда вместо х его значение 2, а вместо dx его значение 0,1, получим Из определения дифференциала функции следует, что дифференциал функции одного переменного является функцией двух переменных. Из формул (5) и (6) следует, что Таким образом, производная равна отношению дифференциала функции к дифференциалу независимого переменного. С этого момента для обозначения производной будем пользоваться и знаком ( )’ и отношением дифференциалов. Таблица дифференциалПрименение к приближенным вычислениямПерепишем формулу (4) § 2 в следующем виде: и для начала посмотрим на примере, как будут выглядеть отдельные ее члены при некоторых числовых значениях х и h. Пример: Пусть С другой стороны, применяя формулу (1) и зная, что Сравнивая формулы (*) и (**), видим, что в левых частях стоит одно и то же, в правых же частях совпадают первые два члена, следовательно, третий член в формуле (**) равен двум последним членам в формуле (*), т. е. Вычислим все члены, встречающиеся в этом примере, при указанных числовых значениях х и h: Если бы мы захотели вычислить Аналогично в общем случае формулу (1) заменяют приближенной формулой, откидывая бесконечно малую высшего порядка, т. е. член а (x, h)h . Тогда получается приближенная формула (знак Приведем примеры применения формулы (2). Пример: Выведем приближенную формулу для вычисления кубического корня. Возьмем Если положить Отсюда видно, что если нам известен кубический корень из числа, то для близких чисел можно с удобством воспользоваться выведенной формулой. Например, зная, что Сделаем проверку, возведя 10,01 в куб. Видим, что вместо 1003 получили число 1003,003001, т. е. ошибка меньше 0,005. Пример: Выведем приближенную формулу для вычисления тангенсов малых углов. Так как Зная, что tg 0 = 0 и cos 0=1, и полагая в предыдущей формуле x = 0, найдем Напоминаем, что здесь h есть радианная мера угла. Например, вычислим tg3°. Переведем сначала градусную меру угла в радианную: Дифференциал площади криволинейной трапецииОпределение: Криволинейной трапецией называется плоская фигура, ограниченная с трех сторон прямыми, а с четвертой стороны кривой. При этом две прямые параллельны между собой и перпендикулярны третьей, а кривая пересекается с любой прямой, параллельной боковым сторонам, в одной точке. Не исключается случай, когда одна или обе боковые стороны обращаются в точку. На рис. 69, 70, 71 изображены криволинейные трапеции. Все плоские фигуры, с которыми нам придется встречаться, могут быть представлены как совокупность криволинейных трапеций. Например, на рис. 72 фигура разбита на четыре криволинейные трапеции. Конечная наша цель — определить площадь криволинейной трапеции, но пока эту задачу мы еще не можем решить. Однако мы сумеем найти дифференциал площади криволинейной трапеции. Решим эту задачу, предполагая, что трапеция расположена определенным образом. Пусть дана криволинейная трапеция АВСD, ограниченная осью Ох, двумя прямыми, перпендикулярными этой оси, и кривой, заданной уравнением у=f(х) (рис. 73). Будем считать, что прямая АВ неподвижна в процессе всех рассуждений, т. е. абсцисса точки А есть постоянная величина. «Прямую же СD будем двигать, т. е. абсцисса точки D будет переменной. Обозначим ее через х. Ясно, что площадь криволинейной трапеции АВСD будет изменяться в зависимости от величины х, значит, площадь есть функция х. Обозначим ее F(х). Этой функции мы не знаем, но несмотря на это найдем ее дифференциал. Дадим х приращение h = DК, тогда площадь F(x) получит приращение При изменении независимого переменного от величины х до х + h (от точки D) до точки К) функция f(х), т. е. ордината точки, лежащей на кривой, также изменяется и при этом достигает наибольшего значения М и наименьшего значения т. На рис. 73 QR = М и NР= т. Рассмотрим прямоугольник с основанием DК и высотой QR = М , его площадь равна Т1= Мh. Прямоугольнике тем же основанием DK = h и высотой NР = т имеет площадь, равную T2 = тh. Очевидно, что площадь второго прямоугольника Т2 меньше площади T1 первого на величину (М— т)h . Также очевидно, что площадь второго прямоугольника меньше приращения Следовательно, приращение Обозначим разность между приращением Величина Остановимся на формуле (1) и проследим, как меняются ее члены при стремлении h к нулю. Предварительно заметим, что, во-первых, всегда, т. е. при любых значениях x, и, во-вторых, если Функция f(х) предполагается непрерывной. В силу свойств непрерывной функции (см. гл. VI, § 6) находим а это значит, что можно записать (см. начало § 2 этой главы) где а—бесконечно малая относительно h. Также можно заключить, что где Исследуем порядок малости членов, стоящих в правой части равенства (1). Для этого найдем следующие пределы: Первый предел находим непосредственно [применяя (3)]: Чтобы найти второй предел, найдем сначала [используя (4) и (5)] Так как а в силу равенства (7) Таким образом, установлено, что и mh и Учитывая все эти рассуждения и применяя равенство (4), можно переписать равенство (1) в виде В правой части равенства (8) стоят три члена. Каждый из них является бесконечно малым относительно h первый из них линеен относительно h, а два других имеют высший порядок малости. Применяя результаты § 2, заключаем, что приращение площади криволинейной трапеции равно f(x)h плюс величина высшего порядка относительно h , а поэтому дифференциал площади криволинейной трапеции равен f(x)h , т. е. Этим результатом мы воспользуемся в следующих главах. Пример: Найдем дифференциал площади F криволинейной трапеции, ограниченной осью Ох, кривой, заданной уравнением Применяя только что полученный результат, будем иметь Пример: Найти производную от площади криволинейной трапеции, ограниченной осью Ох, кривой, заданной уравнением у = sin x, прямой х = 2 и подвижной прямой, параллельной оси Оу. Находим дифференциал этой площади: dF = sin x dx, а следовательно и производную: Применение дифференциала к различным задачамРассуждения не только приводят к понятию дифференциала, но в некоторых случаях позволяют найти производную. Предположим, что приращение некоторой функции представлено в виде где т. е. Пример: Найти производную от функции f(x), определенной геометрически как объем, ограниченный: 1) поверхностью Р, полученной от вращения вокруг оси Ох дуги ОА, принадлежащей параболе 2) плоскостью П1, перпендикулярной оси Ох и отстоящей от начала координат на расстояние х (рис. 74). Ясно, что объем зависит от величины х, т. е. является функцией х . Возьмем произвольное число х. Соответствующее значение функции f(х) будет определяться объемом, ограниченным поверхностью Р и плоскостью П1 . Дадим х приращение h. Объем, т. е. функция f(x), в связи с этим получит приращение Рассмотрим два цилиндра: первый из них имеет основанием К1, образующую, параллельную оси Ох, и высоту h, второй имеет основанием К2 и образующую, также параллельную оси Ох (рис. 77). Объем первого цилиндра обозначим через W1 второго — через W2 . Из чертежей ясно, что приращение функции Но oбъемы W1 и W2 легко подсчитать: Разность объемов W1 и W2 (т. е. объем цилиндрического кольца) равна Приращение где то член В этом примере следует обратить внимание на то, что функция f(х) была определена чисто геометрически, нам не была известна формула, определяющая эту функцию, однако производную мы нашли. Пример: Рассмотрим цилиндрическую трубу, у которой радиус внешней поверхности R, радиус внутренней поверхности r, высота H. Найдем объем V материала, из которого сделана эта труба (рис. 78). Будем называть этот объем объемом цилиндрического слоя. Поскольку объем внешнего цилиндра равен Если стенка трубы тонкая, то r и R мало отличаются друг от друга. Обозначим их разность через h (h = R — r). Тогда формула (*) примет вид Второй член, стоящий в правой части равенства (*), второго порядка относительно h. Поэтому при Интересно отметить еще один способ получения этой формулы (рис. 79). Если разрезать трубку вдоль ее образующей и развернуть на плоскость, то получим «почти» прямоугольный параллелепипед с измерениями Решение заданий и задач по предметам: Дополнительные лекции по высшей математике: Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института Источник |

 определен в некотором классе функций y (x).
определен в некотором классе функций y (x). 
 определяется аналогичным образом:
определяется аналогичным образом:
 , которая обозначается символическим выражением
, которая обозначается символическим выражением  и представляет собой главную линейную часть приращения функционала относительно вариации аргумента:
и представляет собой главную линейную часть приращения функционала относительно вариации аргумента:
 . В таких случаях – и не только в таких – можно использовать равноправное представление вариация функционала J [y (x)] в виде
. В таких случаях – и не только в таких – можно использовать равноправное представление вариация функционала J [y (x)] в виде

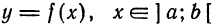 , дифференцируема в некоторой точке
, дифференцируема в некоторой точке 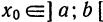 , то ее приращение в этой точке может быть представлено в виде
, то ее приращение в этой точке может быть представлено в виде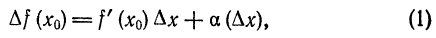
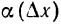 такова, что
такова, что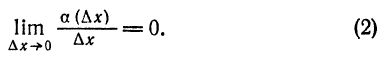
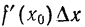 является линейной функцией от
является линейной функцией от 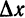 , а слагаемое
, а слагаемое 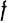 в точке
в точке 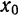 .
.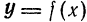 в точке
в точке 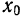 называется линейная относительно
называется линейная относительно 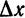 функция
функция 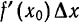 составляющая главную часть приращения функции
составляющая главную часть приращения функции 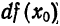 («де эф от икс нулевое) или
(«де эф от икс нулевое) или 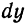 («де игрек»)»
(«де игрек»)»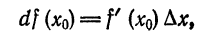

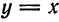 .
.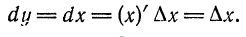
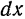 независимого переменного
независимого переменного 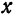 совпадает с его приращением
совпадает с его приращением 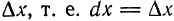 . Поэтому равенство (3) можно записать в виде
. Поэтому равенство (3) можно записать в виде
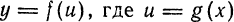 .
.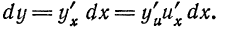
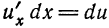 поэтому,
поэтому,
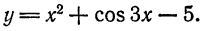
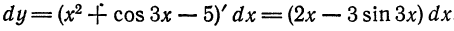

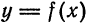 — дифференцируемая в точке
— дифференцируемая в точке 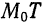 — касательная к графику функции
— касательная к графику функции 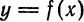 в точке
в точке 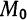 с абсциссой
с абсциссой 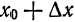 .
.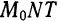 находим
находим 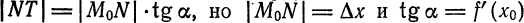 . По этому
. По этому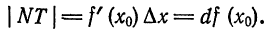
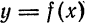 в точке
в точке 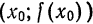 , соответствующему приращению ее абсциссы
, соответствующему приращению ее абсциссы 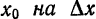 .
.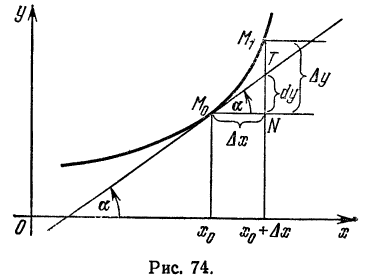
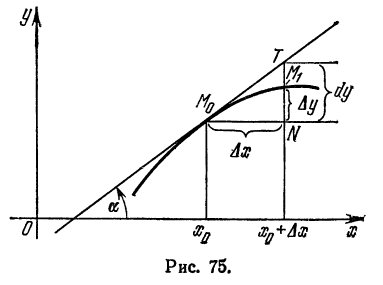
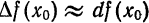 . Этот вывод следует и из равенств (1) и (2) предыдущего параграфа.
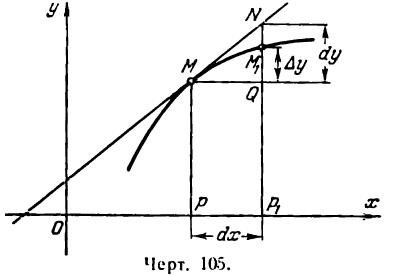
. Этот вывод следует и из равенств (1) и (2) предыдущего параграфа.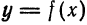 имеет форму
имеет форму
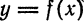 равен произвелдению производной этой функции на дифференциал ее аргумента.
равен произвелдению производной этой функции на дифференциал ее аргумента.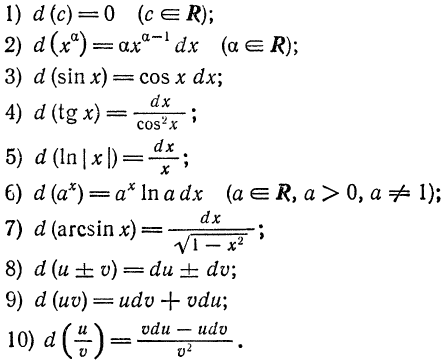
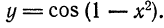
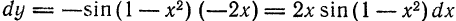
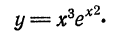
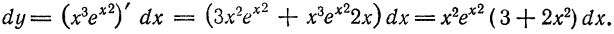
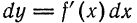 следует, что дифференциал функции
следует, что дифференциал функции 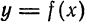 зависит от двух переменных,
зависит от двух переменных, 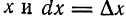 , причем
, причем 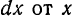 не зависит.
не зависит.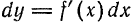 только как функцию от
только как функцию от 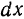 постоянным. В этом случае можно найти дифференциал этой функции.
постоянным. В этом случае можно найти дифференциал этой функции.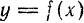 называется дифференциалом второго порядка, или вторым дифференциалом этой функции и обозначается
называется дифференциалом второго порядка, или вторым дифференциалом этой функции и обозначается 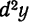 («де два игрек») или
(«де два игрек») или 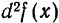 («де два эф от икс»).
(«де два эф от икс»).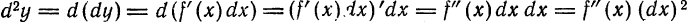
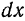 не писать, поэтому
не писать, поэтому
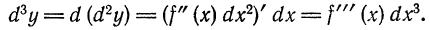
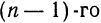 порядка:
порядка: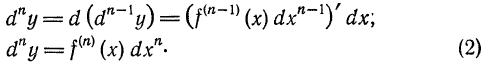
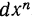 .
.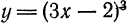
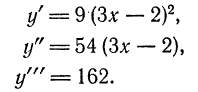
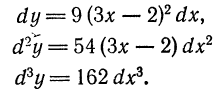
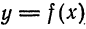 , приращение которой
, приращение которой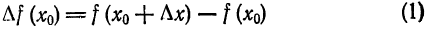
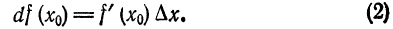
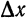 — имеем
— имеем
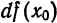 значительно проще, чем
значительно проще, чем 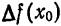 , то на практике формулу (3) применяют к различным приближенным вычислениям.
, то на практике формулу (3) применяют к различным приближенным вычислениям.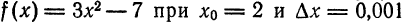 .
.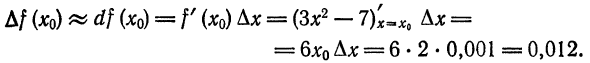
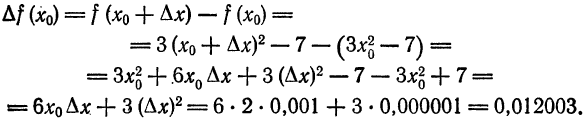
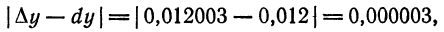
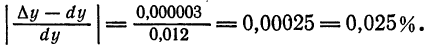
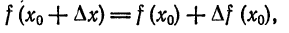
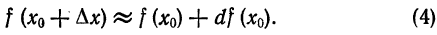
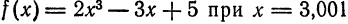
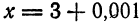 Приняв
Приняв 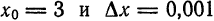 найдем
найдем 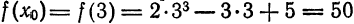
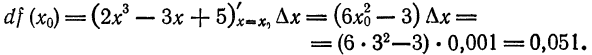
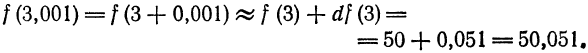
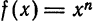 Применив формулу (4), получим
Применив формулу (4), получим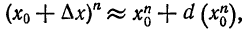
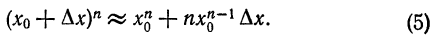
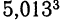 .
.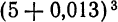 . Приняв
. Приняв 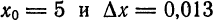 по формуле
по формуле 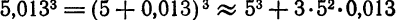
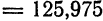
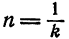 и
и 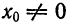 формула (5) примет вид
формула (5) примет вид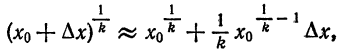
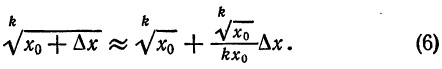
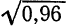
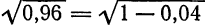 Приняв
Приняв 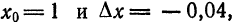 по формуле (6) найдем:
по формуле (6) найдем: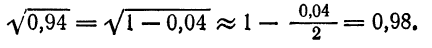













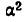 и 2а будут также бесконечно малыми. При делении их друг на друга возможны следующие случаи:
и 2а будут также бесконечно малыми. При делении их друг на друга возможны следующие случаи: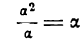 — бесконечно малая величина,
— бесконечно малая величина,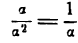 — бесконечно большая величина,
— бесконечно большая величина,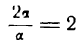 — конечная величина.
— конечная величина.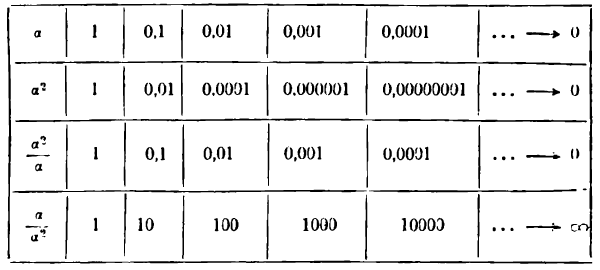
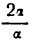 остается постоянным. Такие бесконечно малые имеют, как говорят, одинаковый порядок малости.
остается постоянным. Такие бесконечно малые имеют, как говорят, одинаковый порядок малости.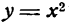 ; ее приращение
; ее приращение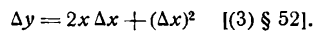
 есть производная данной функции, а потому последнее равенство можно переписать так:
есть производная данной функции, а потому последнее равенство можно переписать так: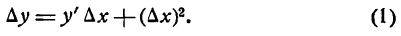

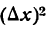 уменьшаются с уменьшением
уменьшаются с уменьшением 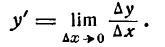
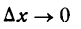 . Отсюда
. Отсюда
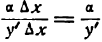 —бесконечно
—бесконечно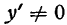 , т. е. по отношению к у’
, т. е. по отношению к у’ 
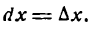


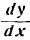 и читают: «дэ игрек по дэ икс».
и читают: «дэ игрек по дэ икс».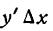 символом dу, напишем:
символом dу, напишем:
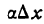 — бесконечно малая высшего порядка по отношению к
— бесконечно малая высшего порядка по отношению к 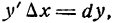 а потому, отбросив в равенстве (6) слагаемое
а потому, отбросив в равенстве (6) слагаемое 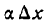 , получим:
, получим:
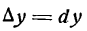 . В самом деле, для функции
. В самом деле, для функции 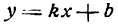 приращение будет:
приращение будет: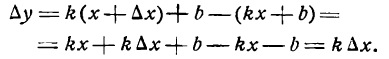
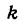 есть производная линейной функции; поэтому правая часть последнего равенства выражает дифференциал данной функции, т. е.
есть производная линейной функции; поэтому правая часть последнего равенства выражает дифференциал данной функции, т. е.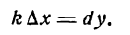
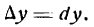
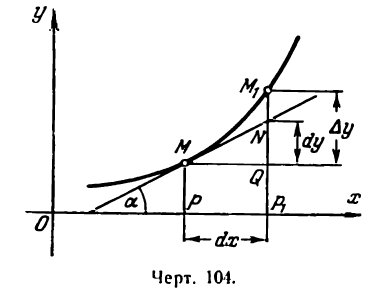
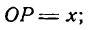
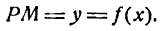
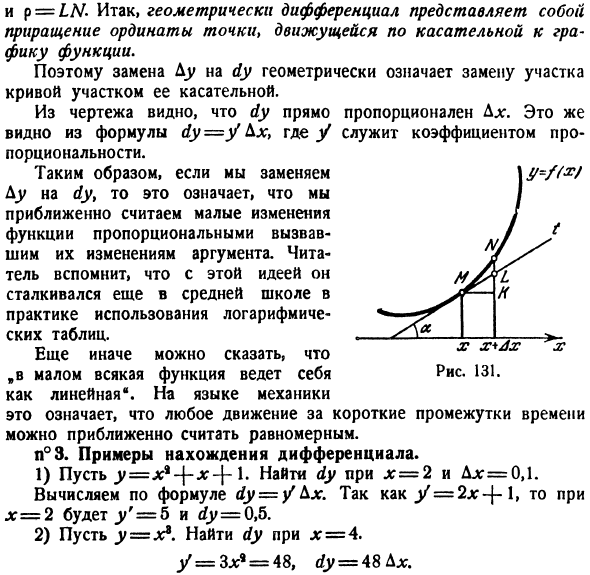
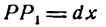 и восставим в точке Р1 перпендикуляр Р1М1 к оси Ох, а из точки М проведем
и восставим в точке Р1 перпендикуляр Р1М1 к оси Ох, а из точки М проведем 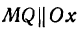 . Тогда, как известно,
. Тогда, как известно,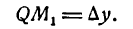
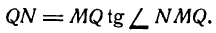
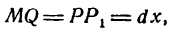
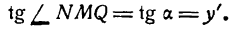
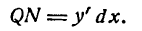
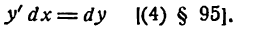
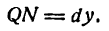
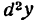 и читают: «дэ два игрек».
и читают: «дэ два игрек».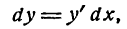
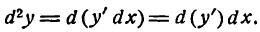
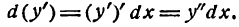
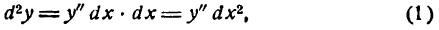
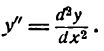
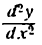 которое читают так: «дэ дна игрек по дэ икс квадрат».
которое читают так: «дэ дна игрек по дэ икс квадрат».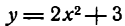
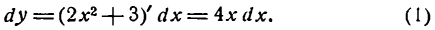
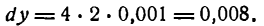
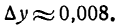
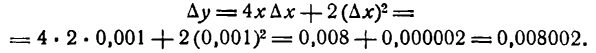
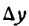 с приближенным, видим, что допущенная ошибка равна 0,000002. Выражая ее в процентах, найдем:
с приближенным, видим, что допущенная ошибка равна 0,000002. Выражая ее в процентах, найдем: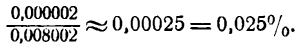
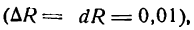
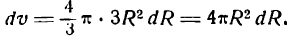
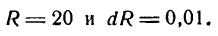
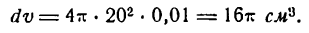
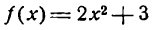
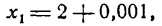
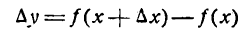
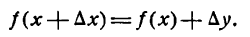
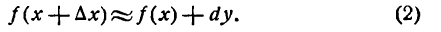
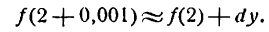
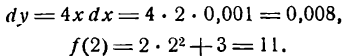
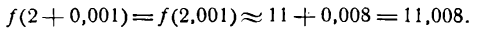
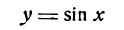
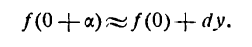
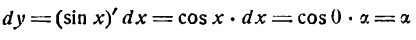
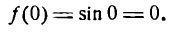
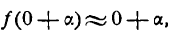
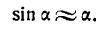
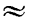 0,003. В самом деле, выразив данный угол в градусной мере, найдем:
0,003. В самом деле, выразив данный угол в градусной мере, найдем: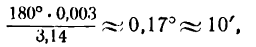
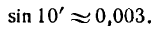
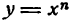 и положим, что х, равный 1, получает весьма малое по сравнению с единицей приращение
и положим, что х, равный 1, получает весьма малое по сравнению с единицей приращение 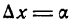 . Тогда согласно формуле (2) имеем:
. Тогда согласно формуле (2) имеем: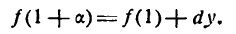
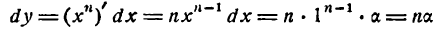
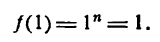
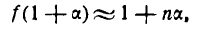

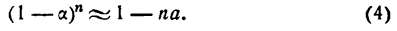
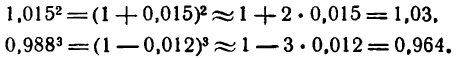
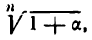 где а имеет малое значение по сравнению с единицей. Для этого представим
где а имеет малое значение по сравнению с единицей. Для этого представим 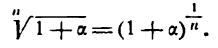
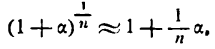
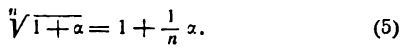
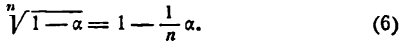
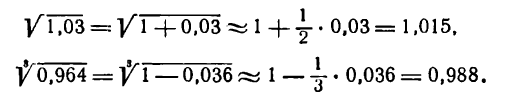
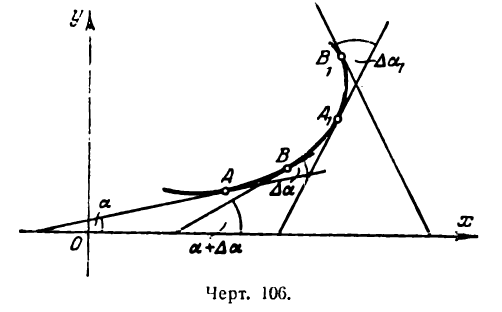
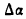 , будет равен а +
, будет равен а + 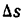 , получим среднюю величину угла отклонения, приходящегося на единицу длины дуги. Отношение
, получим среднюю величину угла отклонения, приходящегося на единицу длины дуги. Отношение 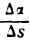 называется средней кривизной кривой на ее участке АВ.
называется средней кривизной кривой на ее участке АВ.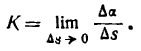
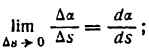

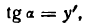
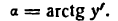
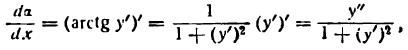

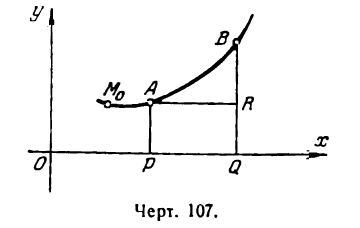
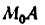 , соответствующее приращениям PQ =
, соответствующее приращениям PQ = 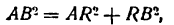
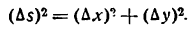
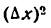 , найдем:
, найдем: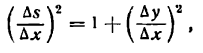
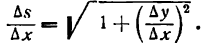
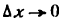 тогда
тогда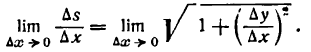
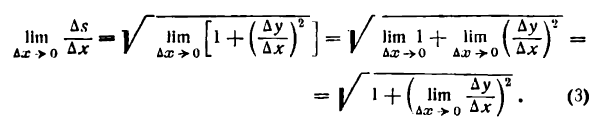
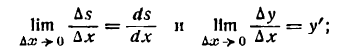
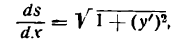
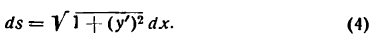
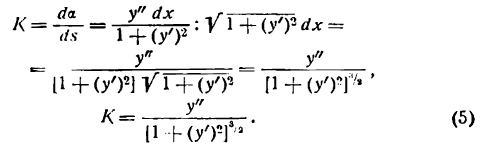
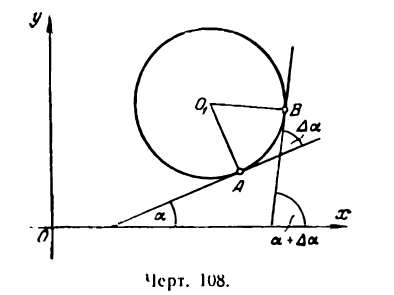
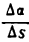 . Проведя радиусы в точки касания, получим:
. Проведя радиусы в точки касания, получим: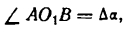
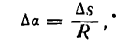
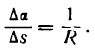
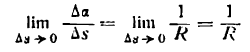
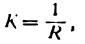
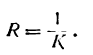
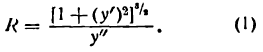
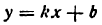 получим:
получим: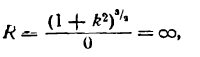
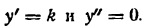
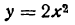 в точке, абсцисса которой равна
в точке, абсцисса которой равна 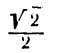
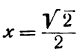
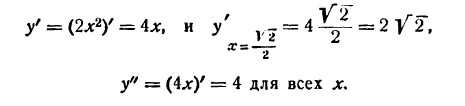
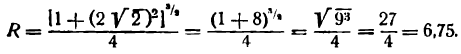
 В этом параграфе чаще всего независимое переменное будем обозначать через h.
В этом параграфе чаще всего независимое переменное будем обозначать через h.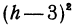 является бесконечно малой величиной при условии, что h стремится к 3; sinh и tgh являются бесконечно малыми при условии, что h стремится к нулю.
является бесконечно малой величиной при условии, что h стремится к 3; sinh и tgh являются бесконечно малыми при условии, что h стремится к нулю. . Таким образом, будем говорить, что sinh , tgh ,
. Таким образом, будем говорить, что sinh , tgh , 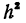 являются «бесконечно малыми», а не бесконечно малыми при условии
являются «бесконечно малыми», а не бесконечно малыми при условии 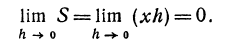
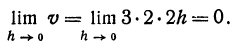
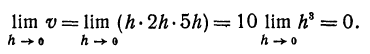
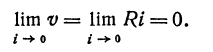
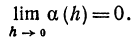
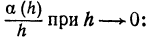
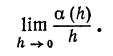
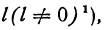 то бесконечно малые a (h) и h называются величинами одного порядка; если l =1, то a(h) и h называются эквивалентными бесконечно малыми.
то бесконечно малые a (h) и h называются величинами одного порядка; если l =1, то a(h) и h называются эквивалентными бесконечно малыми.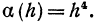 Это бесконечно малая величина порядка более высокого, чем h, так как
Это бесконечно малая величина порядка более высокого, чем h, так как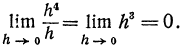
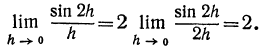
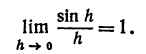
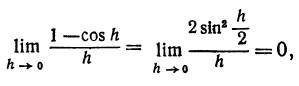
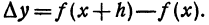
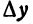 нужно задать величину х и величину h , т. е. приращение функции одного переменного является функцией двух независимых переменных х и h .
нужно задать величину х и величину h , т. е. приращение функции одного переменного является функцией двух независимых переменных х и h .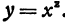 Ее приращение равно
Ее приращение равно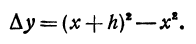
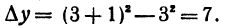
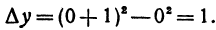
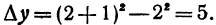
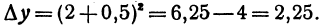
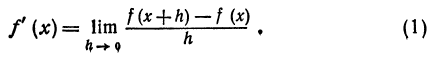
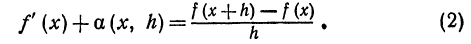

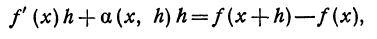
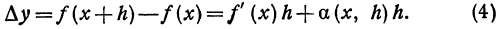
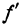 (x)h и а(x , h)h . Оценим порядок малости этих членов:
(x)h и а(x , h)h . Оценим порядок малости этих членов: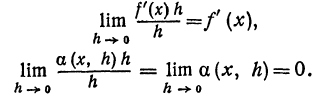
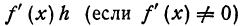
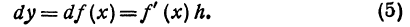

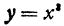 ,если x = 2 и dx = h = 0,1 .
,если x = 2 и dx = h = 0,1 .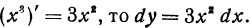
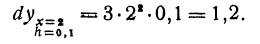
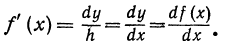

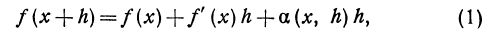
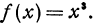 Положим x = 2 и h = 0,01. Применяя формулу куба суммы, получаем
Положим x = 2 и h = 0,01. Применяя формулу куба суммы, получаем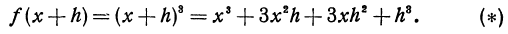
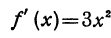 получим
получим
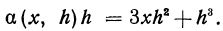
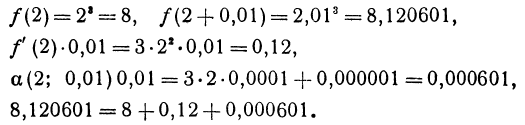
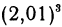 не точно, а приближенно с точностью до 0,01, то член а (x, h)h = 0,000601 никакого значения бы не имел, т. е. его можно было бы просто откинуть.
не точно, а приближенно с точностью до 0,01, то член а (x, h)h = 0,000601 никакого значения бы не имел, т. е. его можно было бы просто откинуть.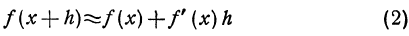
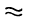 обозначает приближенное равенство). Эту формулу имеет смысл употреблять только при малых значениях величины h, так как в противном случае ошибка может оказаться очень большой.
обозначает приближенное равенство). Эту формулу имеет смысл употреблять только при малых значениях величины h, так как в противном случае ошибка может оказаться очень большой.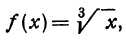 тогда
тогда 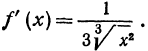 Применяя формулу (2), получаем
Применяя формулу (2), получаем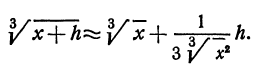
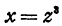 , то полученному результату можно придать следующий вид:
, то полученному результату можно придать следующий вид: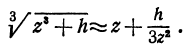
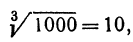 вычисляем
вычисляем 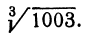 Здесь z = 10, h = 3, поэтому получаем
Здесь z = 10, h = 3, поэтому получаем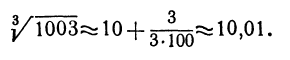
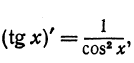 то применяя формулу (2), получаем
то применяя формулу (2), получаем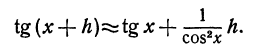
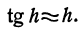
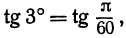
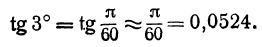
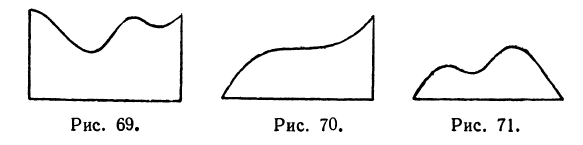
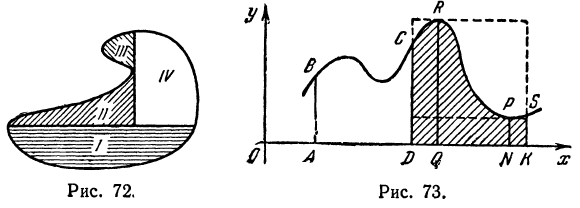
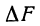 ( х ) (это приращение на рис. 73 заштриховано).
( х ) (это приращение на рис. 73 заштриховано).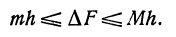

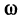 меняется вместе с h и всегда меньше (М— т)h . Обозначим через
меняется вместе с h и всегда меньше (М— т)h . Обозначим через 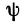 ) разность между площадью Т1 и приращением
) разность между площадью Т1 и приращением 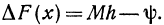

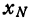 , заключена между D и К, поэтому при
, заключена между D и К, поэтому при 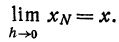
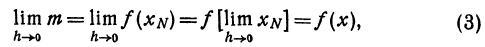


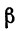 —бесконечно малая относительно h.
—бесконечно малая относительно h.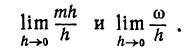
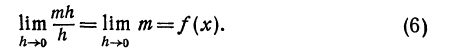
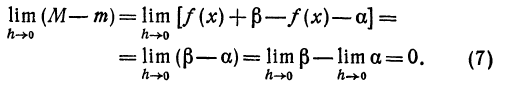
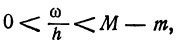
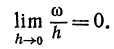
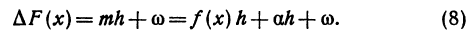
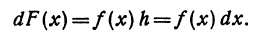
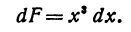
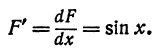
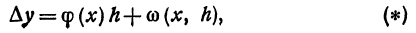
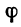 (x) не зависит от h, и
(x) не зависит от h, и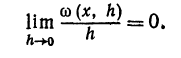
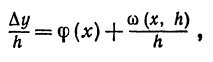
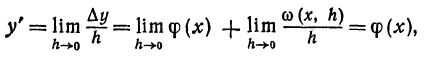
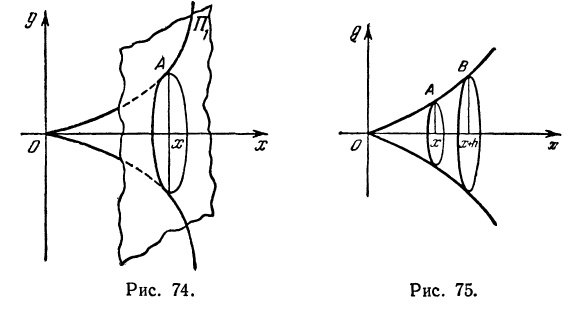
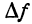 . Это приращение показано на рис. 75 и отдельно на рис. 76: оно ограничено поверхностью Р и плоскостями П1 и П2. Плоскости П1 и П2 пересекаются с поверхностью Р по окружностям (так как Р—поверхность вращения). Обозначим эти окружности К1 и К2.
. Это приращение показано на рис. 75 и отдельно на рис. 76: оно ограничено поверхностью Р и плоскостями П1 и П2. Плоскости П1 и П2 пересекаются с поверхностью Р по окружностям (так как Р—поверхность вращения). Обозначим эти окружности К1 и К2.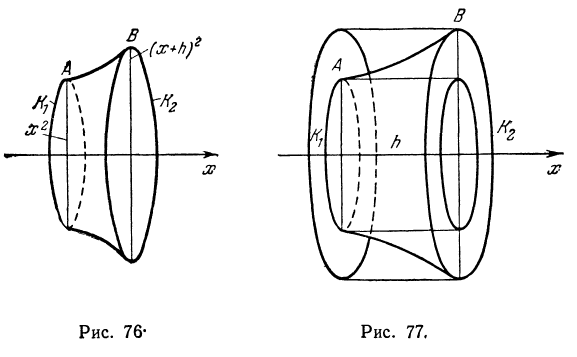
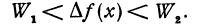
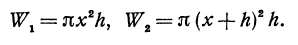
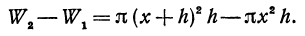
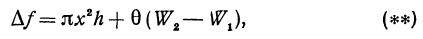
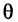 — некоторое положительное число, меньшее единицы. Так как
— некоторое положительное число, меньшее единицы. Так как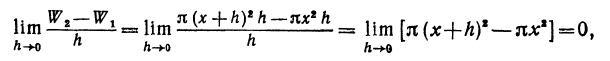
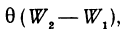 —стоящий в правой части равенства (**), является бесконечно малой высшего порядка малости относительно h. Поэтому равенство (**) является частным случаем равенства (*). Следовательно, вывод, который был сделан в начале параграфа, может быть перенесен и на равенство (*), т. е. производная от функции f(х) равна
—стоящий в правой части равенства (**), является бесконечно малой высшего порядка малости относительно h. Поэтому равенство (**) является частным случаем равенства (*). Следовательно, вывод, который был сделан в начале параграфа, может быть перенесен и на равенство (*), т. е. производная от функции f(х) равна 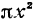 .
.
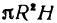 , а объем внутреннего равен
, а объем внутреннего равен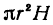 , то объем цилиндрического слоя равен
, то объем цилиндрического слоя равен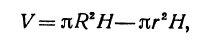
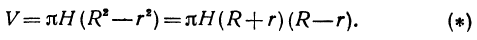
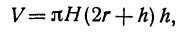
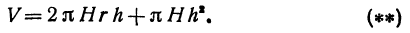
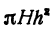 становится бесконечно малой высшего порядка. Отбрасывая его, мы получим приближенную формулу для подсчета объема тонкого цилиндрического слоя:
становится бесконечно малой высшего порядка. Отбрасывая его, мы получим приближенную формулу для подсчета объема тонкого цилиндрического слоя: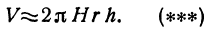
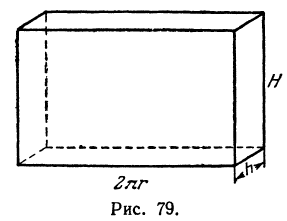
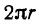 , h и H. Его объем равен
, h и H. Его объем равен 



