Что значит кубический корень

Кубический корень

Куби́ческий (куби́чный) ко́рень из a — решение уравнения (обычно подразумеваются вещественные решения). Операция извлечения кубического корня эквивалентна операции возведения числа в степень, при условии, что число неотрицательно. [источник не указан 107 дней] .

Содержание

Свойства

Кубический корень — нечётная функция. В отличие от квадратного корня, кубический может быть извлечён и из отрицательных чисел:

Общее правило — из отрицательных чисел корни нечётной степени (в том числе и кубический) извлекаются, корни чётной степени — нет. Данное утверждение справедливо только для диапазона вещественных чисел.

Кубический корень из комплексного числа (из любого числа) имеет ровно три значения (частный случай свойства корня n-ой степени):

Здесь под понимается арифметический корень из положительного числа

Два комплексных значения кубического корня получаются из вещественных по формуле:

Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.

Интересные факты

Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.

При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26%) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.

См. также

Литература

• Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М .: Наука, 1978. — С. 32—33.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Кубический корень» в других словарях:

кубический корень — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN third root … Справочник технического переводчика

КУБИЧЕСКИЙ — (от слова куб). 1) имеющий вид куба. 2) мера, имеющая форму куба, т. е. правильного шестигранника. 3) корень, всякая величина, которая, будучи помножена три раза сама на себя, дает данную величину. Словарь иностранных слов, вошедших в состав… … Словарь иностранных слов русского языка

КОРЕНЬ КУБИЧЕСКИЙ — (обозначение 3Ц), число, которое необходимо дважды умножить на само себя для получения заданного числа. Например, кубический корень из 64 равняется 4, поскольку 4x4x4 = 64. В этом случае записывают: 3Ц64 = 4. В терминах алгебры кубический корень… … Научно-технический энциклопедический словарь

кубический — КУБИЧЕСКИЙ, КУБИЧНЫЙ ая, ое. cubique adj. <, лат. cubicus. 1. Имеющий форму куба. шестигранника. Сл. 18. Большая голова кубической фигуры. С. Меран 20. Горница имела совершенно кубический вид. ТВЭО 50 14. 2. Связанный с объемом, измерением… … Исторический словарь галлицизмов русского языка

КОРЕНЬ — КОРЕНЬ, корня, мн. корни, корней, м. 1. Вросшая в землю часть растения, через к рую оно всасывает соки из почвы. Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь Ушакова

КУБИЧЕСКИЙ — КУБИЧЕСКИЙ, кубическая, кубическое. 1. прил. к куб1 в 1 и 4 знач. (мат.). Кубическая форма. Кубическая степень. Извлечь кубический корень. 2. Выраженный в мерах, за единицу объема которых принят куб. Кубическая система мер. Кубический метр.… … Толковый словарь Ушакова

КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь

Корень (значения) — Корень: В Викисловаре есть статья «корень» Корень (в ботанике) вегетативный осевой подземный орган растения, обладающий сп … Википедия

корень — сущ., м., употр. сравн. часто Морфология: (нет) чего? корня, чему? корню, (вижу) что? корень, чем? корнем, о чём? о корне и на корню; мн. что? корни, (нет) чего? корней, чему? корням, (вижу) что? корни, чем? корнями, о чём? о корнях 1. Корень это … Толковый словарь Дмитриева

Кубический закон взаимности — Характер кубического вычета – теоретико числовая функция двух аргументов, являющаяся частным случаем символа степенного вычета. Также является характером в простом поле. Характер кубического вычета является аналогом символа Лежандра, и для его… … Википедия

Источник

Как извлекать кубические корни в уме

Как-то раз британскому министру образования в телеинтервью 10-летняя девочка задала вопрос: «назовите кубический корень из 125». Министр не ответила и сказала, что не будет отвечать ни на какие вопросы, связанные с математикой.

С одной стороны её можно понять. А с другой стороны, знай она простое правило, о котором я сегодня расскажу, она бы не попала в такую ситуацию. Впрочем, многие небезосновательно считают, что не знать кубический корень из 125 просто стыдно.

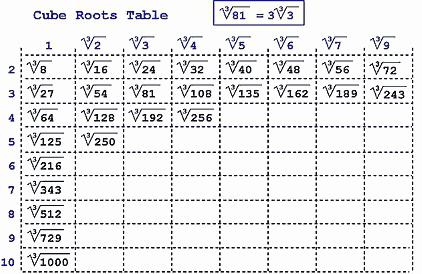
Итак, чтобы считать кубические корни, мы должны знать кубики (так я называю число в кубе) чисел от 1 до 10 . Большинство их и так знает. И сразу обратим внимание на то, какой цифрой они заканчиваются.

Тут надо заметить интересную вещь. Куб чисел 1, 4, 5, 6, 9 и 0 или 10 заканчивается на само число. А числа 2 и 8 и 3 и 7 следует запоминать парами. То есть куб двойки заканчивается на 8, а куб восьмерки — на 2. И с 3 и 7 то же самое: куб тройки заканчивается на 7, а куб семерки — на 3.

Давайте извлечём кубический корень из числа 39 304

Шаг первый

Смотрим, на что оканчивается число 39304? На цифру 4. Это соответствует четверке (смотри табличку выше). Запоминаем эту цифру или где-то записываем (это будет последний цифрой в искомом числе).

Шаг второй

Теперь проигнорируем последние 3 цифры нашего числа и найдем ближайший к этому числу куб, не превосходящий его.

Игнорируем три последние цифры — 39 304 . Осталось 39. Это число располагается между 27=3³ и 64=4³. Но так как нам нужен куб, не превосходящий число, то нас устраивает только 27. Это куб трёх. Поэтому второй цифрой, которую мы запоминаем (или записываем) будет тройка. Пишем её левее четверки и получаем число 34.

На самом деле всё, потому что 34³=39304 . Легко и просто!

Теперь извлечем кубический корень из числа 636 056

Шаг первый

Число заканчивается на 6. Это соответствует шестерке, так как 6 ³=25 6 . Запоминаем шестерку.

Шаг второй

Зачеркиваем три последние цифры и смотрим на оставшиеся три. 636 056 -> 636. Ближайший к этому числу куб, не превосходящий его — 512. Следующий куб —729, он уже больше 636.

512=8³, поэтому второе число, которое мы должны запомнить — 8. Объединяем оба числа и получаем 86. И в самом деле 86³=636056 .

Где это пригодится?

Например, чтобы провести математический фокус. Попросите друга загадать какое-то двухзначное число про себя и никому его не говорить. Теперь пусть он возведет его в куб и скажет вам результат. А вы спустя пару секунд назовете ему загаданное им число. Уверен, что у вас это получится сделать в уме гораздо быстрее, чем он будет дважды умножать число само на себя столбиком на листочке.

Ещё это может пригодиться, чтобы удивить учительницу. Ну или для того, чтобы сэкономить время на ЕГЭ. Хотя последнее очень сомнительно. В школе не учат извлекать кубические корни в уме, поэтому и заданий там таких нет.

Не забывайте подписываться на мои каналы в Ютубе , Инстаграме и ТикТоке . И, конечно, буду рад, если вы поставите лайк и напишете в комментариях, знали ли вы о таком способе или нет. А если поделитесь публикацией в своих соцсетях, то сильно поможете моему каналу стать популярнее.

Источник

Корни и степени

Степенью называется выражение вида .

Здесь — основание степени, — показатель степени.

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

Возвести число в куб — значит умножить его само на себя три раза.

Возвести число в натуральную степень — значит умножить его само на себя раз:

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

Это верно для . Выражение 0 0 не определено.

Определим также, что такое степень с целым отрицательным показателем.

Конечно, все это верно для , поскольку на ноль делить нельзя.

Заметим, что при возведении в минус первую степень дробь переворачивается.

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .

Выражение всегда неотрицательно, т.е. . Например, .

Свойства арифметического квадратного корня:

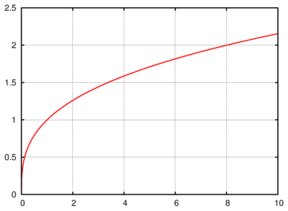
Кубический корень

Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .

Например, , так как ;

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня -ной степени для любого целого .

Корень -ной степени

Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

Сразу договоримся, что основание степени больше 0.

Выражение по определению равно .

При этом также выполняется условие, что больше 0.

Запомним правила действий со степенями:

— при перемножении степеней показатели складываются

— при делении степени на степень показатели вычитаются

— при возведении степени в степень показатели перемножаются

Ты нашел то, что искал? Поделись с друзьями!

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Простые и не очень способы того, как вычислить кубический корень

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.

Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».

В-третьих, для них справедливы все действия со степенями.

• Их можно перемножать. Тогда показатели степеней складываются.
• Корни можно разделить. Степени нужно будет вычесть.
• И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

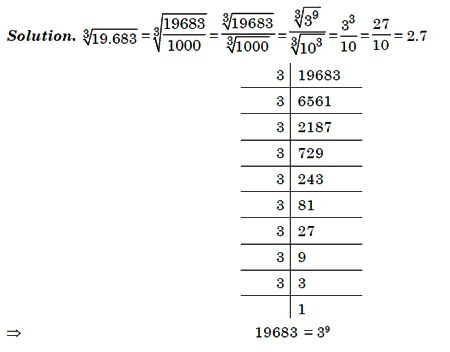
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

1. Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
2. Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
3. Выполнить вычитание.
4. К остатку приписать первую группу цифр после запятой.
5. В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
6. Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
7. Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

1. 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
2. После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
3. а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3 2 + х 3 2 + х 3 2 + х 3

Источник