Что значит кратных семи

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Кратное число — это .

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

1. Делимое – то число, которое собираются делить;
2. Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
3. Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

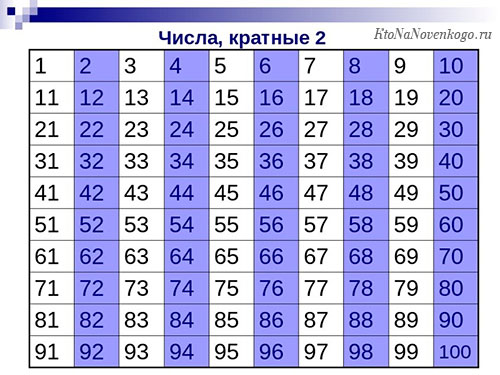
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

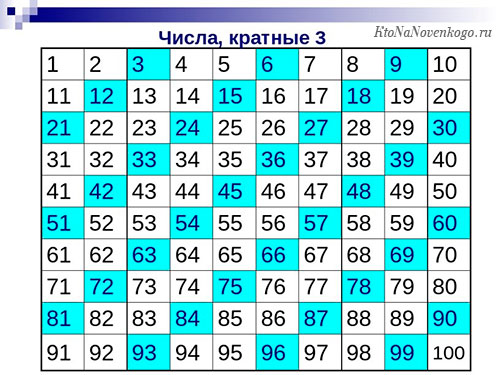
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

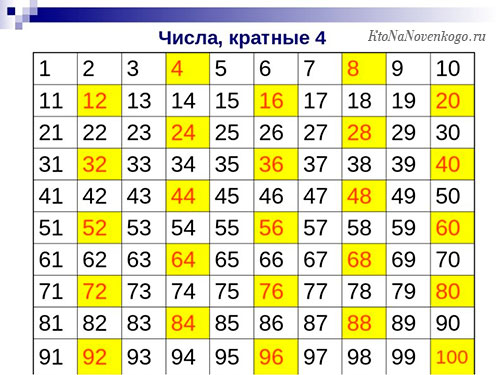
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

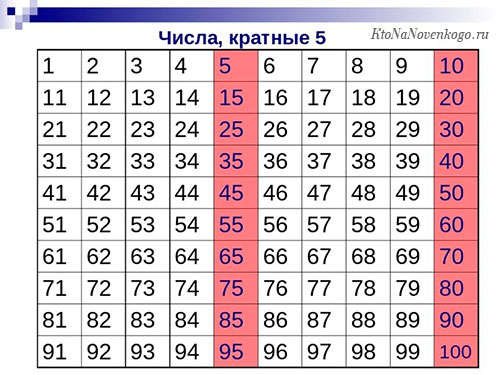
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

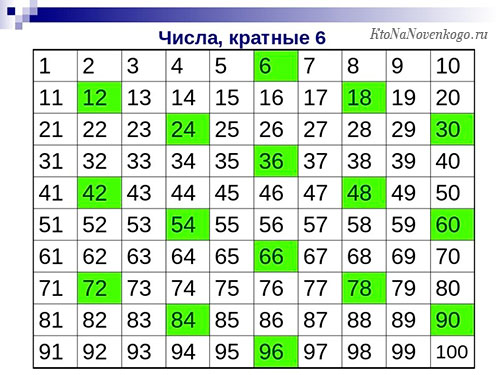
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

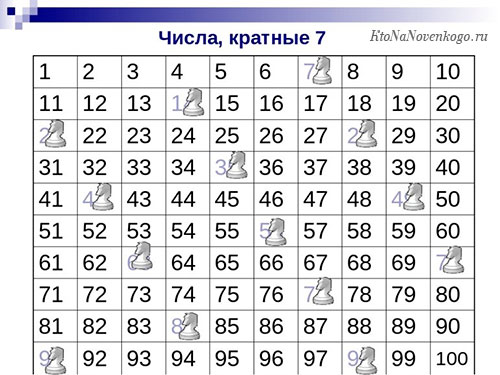
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Числа, кратные 9	27	198	5 877	3 816	117	72
Сумма	9	18	27	18	9	9

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Запишите по порядку, начиная с наименьшего, несколько чисел, кратных 7

Ответ или решение 2

Кратное — это число. которые делится на данное число без остатка.

Самое меньшее числу это и есть это число, значит наименьшее кратное 7 — 7.

Для того чтобы написать ряд чисел, мы будем умножать 7 на натуральный ряд начиная с 1.

Ряд чисел кратных 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70 т.д.

Какие числа называются кратными данному числу

Пусть нам дано некоторое число a. Все числа, на которые делится число a нацело (без остатка), называются кратными числу a. Например, если нам дано число 3, то кратные ему числа — это числа 3 и 1, так как все остальные числа делятся на 3 только с остатком. Необходимо запомнить несколько правил:

• Любое число всегда делится на 1.
• Любое число всегда делится само на себя.
• Числа, которые делятся только на 1 и сами на себя — это простые числа.
• Числа, которые делятся на 1, сами на себя и ещё на какие-то числа — это составные числа.

Какие числа кратны 7

В нашей задаче нам необходимо найти несколько чисел, которые кратны 7, то есть те числа, которые нацело делятся на 7. Запишем несколько таких чисел. Конечно, первое и самое маленькое число — это 7, так как 7/7 = 1. Для дальнейшего выбора чисел, нам необходимо только лишь увеличивать число 7 на 7. Получаем числа, кратные 7:
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105. (ряд можно продолжить бесконечно).

Источник

кратность 7 и циклическое число 142857

Поговорим о числах и цифрах.
Все четные числа кратны двум, но цифра 6 стоит особняком, по той причине,что это единственное натуральное число, до десяти, кратное нечетному-3.
6 обладает сходимостью как для четных, так и для нечетных чисел.
Нечетные числа ведут себя менее предсказуемо,чем четные.
Их кратность гораздо более сложная.
Единице кратны все без исключения числа.
3 кратны числа, кратные 6 и 9 и в ряде случаев числа, кратные 4 и 5.
5 кратны десятки и имеющие 5 на конце.
6 кратна 2 и 3
9 кратна 3
Кратность, геометрия, симметрия чисел закономерна и красива,но самой интересной пожалуй, стоит назвать цифру 7.
Так как, деление на 7, порождает знаменитое число 142857
Из числа 142857 изгнаны нечетные цифры 3,6 и 9, связанные общими закономерностями кратности.
0/7 =0
1/7 =0.142857(142857. )
2/7 =0.285714 (28571. )
3/7 =0.428571(42857. )
4/7 =0.571428
5/7 =0.714285
6/7 =0.857142
7/7 =1.
8/7 =1.142857
9/7 =1.285714
10/7=1.428571
11/7=1.571428
12/7=1.714285
13/7=1.857421
14/7=2.
.
22/7=3.14285714285 — число, ближайшее к числу Пи 3,141592653589793238462643.
Шаг кратности 142857, является периодом разложения обыкновенной дроби 1/7 в десятичную дробь.
Дробь 1/7 — первая обратная величина с максимальным периодом в десятичной записи (длина периода на единицу меньше знаменателя дроби).
Разложенное на множители число 142857 выглядит так:
3 в третьей степени х 11 х 13 х 37
Число 142857, это так называемое число Харшад, Нивена или «Великая радость»,
— натуральное число, делящиеся нацело на сумму своих цифр
142857=5291 х(1+4+2+8+5+7)
https://ru.wikipedia.org/wiki/
А так же, оно является числом Капрекара
142857 в квадрате=200408122449
142857=20408+122449
https://ru.wikipedia.org/wiki/
Соотношение сторон листа формата А4 является десятичной дробью с периодом, равным нашему числу. Так стандартная длина листа А4 равняется 297 мм, а ширина составляет 210 мм. Пропорция, равная отношению длины к ширине листа, выглядит следующим образом 297/210 = 1,4(142857).
Умножим число 142857 на 7, в результате получится 999999. Значит, число 142857 не что иное, как седьмая часть 999999; и, следовательно, дробь 142857/999999 = 1/7. Действительно, если станете превращать 1/7 в десятичную дробь,

142 857 х 1 = 142 857
142 857 х 2 = 285 714
142 857 х 3 = 428 571
142 857 х 4 = 571 428
142 857 х 5 = 714 285
142 857 х 6 = 857 142
Одни и те же цифры меняют свое положение, движутся, как лента.
А 142 857 х 7?
999 999!
Если сложить 142 и 857, получится 999.
428+571=999
285+714=999
857+142=999

14 28 57 = 99
142 857 в квадрате дает 20 408 122 449; 20 408 и 122 449 – две части этого числа. Если их сложить, получится… 142 857.

1/7=142857
13/91=142857
69/91=0,758241 — перевернутое число.
758+241=999
78/91=0,854142
Гурджиев использовал число 142857 в эннеаграмме, для визуализации динамики взаимодействия двумя великими законами Вселенной. Законом Трех и Законом Семи.
Последующие движения эннеаграммы, он использовал в своих священных танцах.
Последованное чередование цифр — есть спиралевидное вращение.
)___________________________
Все великолепие этого мироздания Бог произвел за шесть дней из ничего в украшение величества Своего, седьмой же освятил благословением (см. Быт;2:2–3). Следовательно, поскольку седмеричным числом дней управляется все земное и небесное, потому в качестве введения я буду размышлять об этой неделе, которая царица всех недель, и, насколько смогу, я попытаюсь объяснить день силы (см. Пс;109:3) в его завершении.
fabrica mundi)
Долгое время считалось, что трактат «О сотворении мира» (De fabrica mundi) всего лишь фрагмент одного из многочисленных комментариев свт. Викторина Петавийского (ок. 230–303304), возможно, на книгу Бытия. В последнее время исследователи пришли к убеждению, что это самостоятельное произведение. Впервые публикуется русский перевод с латинского языка этого трактата, выполненный Н.А. Хандогой.

Источник

кратность 7 и циклическое число 142857

Поговорим о числах и цифрах.
Все четные числа кратны двум, но цифра 6 стоит особняком, по той причине,что это единственное натуральное число, до десяти, кратное нечетному-3.
6 обладает сходимостью как для четных, так и для нечетных чисел.
Нечетные числа ведут себя менее предсказуемо,чем четные.
Их кратность гораздо более сложная.
Единице кратны все без исключения числа.
3 кратны числа, кратные 6 и 9 и в ряде случаев числа, кратные 4 и 5.
5 кратны десятки и имеющие 5 на конце.
6 кратна 2 и 3
9 кратна 3
Кратность, геометрия, симметрия чисел закономерна и красива,но самой интересной пожалуй, стоит назвать цифру 7.
Так как, деление на 7, порождает знаменитое число 142857
Из числа 142857 изгнаны нечетные цифры 3,6 и 9, связанные общими закономерностями кратности.
0/7 =0
1/7 =0.142857(142857. )
2/7 =0.285714 (28571. )
3/7 =0.428571(42857. )
4/7 =0.571428
5/7 =0.714285
6/7 =0.857142
7/7 =1.
8/7 =1.142857
9/7 =1.285714
10/7=1.428571
11/7=1.571428
12/7=1.714285
13/7=1.857421
14/7=2.
Шаг кратности 142857, является периодом разложения обыкновенной дроби 1/7 в десятичную дробь.
Дробь 1/7 — первая обратная величина с максимальным периодом в десятичной записи (длина периода на единицу меньше знаменателя дроби).
Разложенное на множители число 142857 выглядит так:
3 в третьей степени х 11 х 13 х 37
Число 142857, это так называемое число Харшад, Нивена или «Великая радость»,
— натуральное число, делящиеся нацело на сумму своих цифр
142857=5291 х(1+4+2+8+5+7)
https://ru.wikipedia.org/wiki/
А так же, оно является числом Капрекара
142857 в квадрате=200408122449
142857=20408+122449
https://ru.wikipedia.org/wiki/
Соотношение сторон листа формата А4 является десятичной дробью с периодом, равным нашему числу. Так стандартная длина листа А4 равняется 297 мм, а ширина составляет 210 мм. Пропорция, равная отношению длины к ширине листа, выглядит следующим образом 297/210 = 1,4(142857).
Умножим число 142857 на 7, в результате получится 999999. Значит, число 142857 не что иное, как седьмая часть 999999; и, следовательно, дробь 142857/999999 = 1/7. Действительно, если станете превращать 1/7 в десятичную дробь,

142 857 х 1 = 142 857
142 857 х 2 = 285 714
142 857 х 3 = 428 571
142 857 х 4 = 571 428
142 857 х 5 = 714 285
142 857 х 6 = 857 142
Одни и те же цифры меняют свое положение, движутся, как лента.
А 142 857 х 7?
999 999!
Если сложить 142 и 857, получится 999.
14 28 57 = 99
142 857 в квадрате дает 20 408 122 449; 20 408 и 122 449 – две части этого числа. Если их сложить, получится… 142 857.
Гурджиев использовал число 142857 в эннеаграмме, для визуализации динамики взаимодействия двумя великими законами Вселенной. Законом Трех и Законом Семи.
Последующие движения эннеаграммы, он использовал в своих священных танцах.

Если число 142 857 разделить последовательно на 11… а результат12987 на 13… то получится число 999

Источник