Что значит кратное 3 или 5

HOWS.RU

Программирование, Seo, Linux, Скрипты, Программы

Сложите все натуральные числа до тысячи, кратные 3 или 5

Давно не писал. Сегодня выходной и я решил начать, время от времени решать задачи с проекта Эйлера. Эти задачи помогут больше понять язык программирования и математику.

В этой задачи и следующих задач, я попытаюсь делать решения на двух языках программирования, на языке Си и на языке Python. Эта задача простая, но все же я решил начать с нее, наверника новичкам она поможет.

Для тех кто не знает, что такое натуральные числа — это числа которые начинаются с 1,2,3,4… и до бесконечности. А кратные числа 3 и 5 — это такие числа, которые делятся на 3 и на 5 с остатком 0. Тоесть 15:3=5, здесь остаток 0, значит число 15, кратное 3. Теперь я попробую решить эту задачу на языке Python:

Для начала давайте выведем на печать все натуральные числа до тысячи кратные 3:

Пример вывода последних чисел:

Далее давайте выведем на печать все натуральные числа до тысячи кратные 5:

Пример вывода последних чисел:

Программа выполнялась в Python 3.3.1 под ОС Arch

В Python % означает остаток от деления, а функция range(1,1001), формирует Python список [1,2,3,4,5,6..]

Можно было записать все вручную, например:

Теперь давайте выведем Все натуральные числа до тысячи кратные 3 или 5:

Вывод на печать будет такой:

В этом куске кода мы добавили оперетор or, который означает или, тоесть мы говорим программе, выводи на печать число которое делится на 3 и у которого остаток от деления 0 или выводи число которое делится на 5 и у которого остаток от деления 0.

Также вместо or, мы могли использовать другие операторы, такие как and.

Теперь давайте до конца доделаем нашу задачу, код получится следующий:

На экран выведет это число:

Здесь мы добавили новую переменную и просто все числа складывали внутри цикла и условия. Теперь получим тоже самое на языке Си:

Получили тоже самое число: 234168

Теперь посмотрим какие изменения в коде языка си. Добавили заголовочный файл stdio.h.

Также в начале объявили переменные и присвоили им тип, оператор or заменился другим оператором ||, прибавление мы сделали через +=. Практически тоже самое.

В си я делал компилирование с помощью cc zadacha.c далее запускал ее как ./a.out. Если вы на windows, то компилируйте и запускайте в ide dev-c++, не забыв подключить сишный компилятор.

Дата публикации: Среда, Май 1st, 2013.

Источник

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Кратное число — это .

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

1. Делимое – то число, которое собираются делить;
2. Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
3. Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

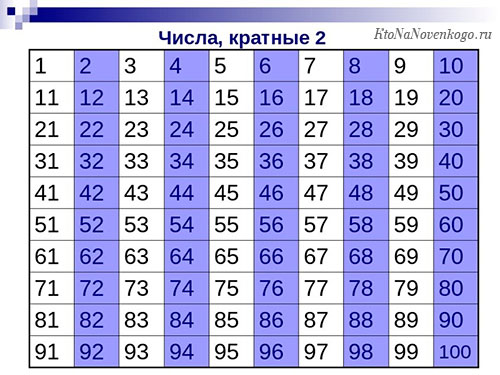
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

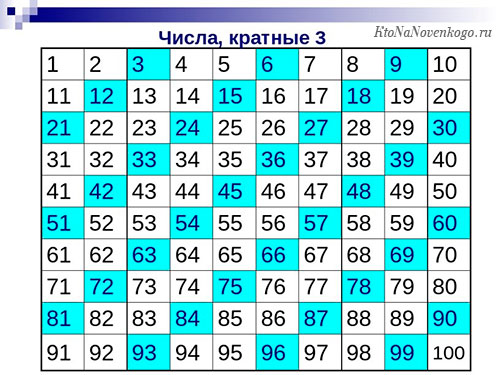
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

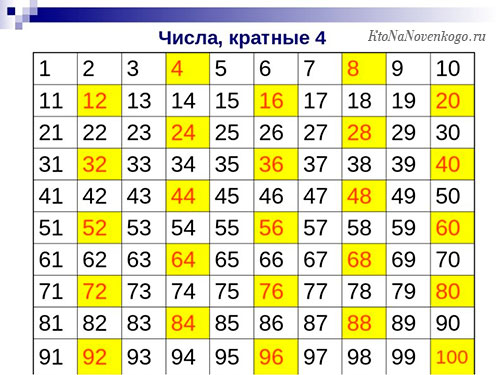
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

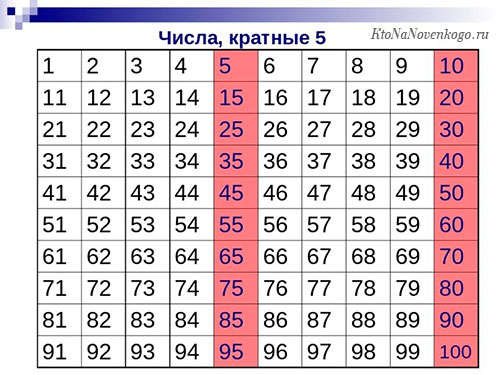
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

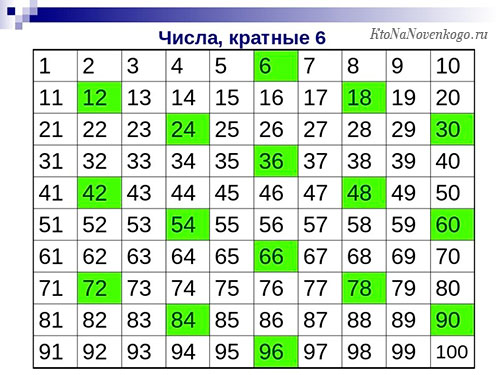
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

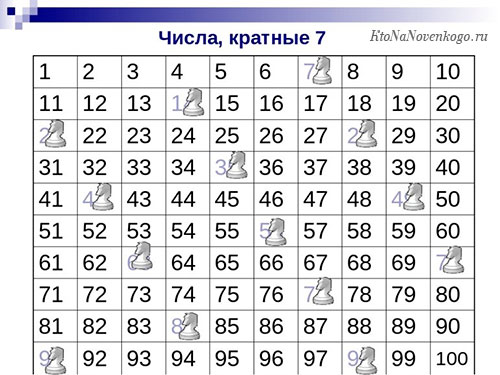
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Числа, кратные 9	27	198	5 877	3 816	117	72
Сумма	9	18	27	18	9	9

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Признаки делимости чисел

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

• Число «0» считается четным числом.

• 0, 8, 24, 66, 88, 100, 120 — чётные.

• 1, 7, 31, 75, 91, 111, 311 — нечётные.

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

• Число 51352 можно разделить на 2, так как последняя цифра (2) делится на 2 без остатка.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

• 20715 можно поделить на 3, так как 2 + 0 + 7 + 1 + 5 = 15 делится на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

• 84100 делится на 4, так как в конце стоят два нуля.
• Число 5324 и 1108 тоже делятся на 4, так как последние цифры образуют числа (24 и 08), которые делятся на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

• 540 и 545 делятся на 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

• Число 612 делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

• 43000 делится на 8, так как 43(000) оканчивается нулями
• 8128 — тоже делится на 8: последние три цифры образуют число 128, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

• 1737 — сумма цифр 1 + 7 + 3 + 7 = 18. 18 делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

• 890 делится на 10.
• 1200 делится на 100.

У нас есть очень крутая статья — деление в столбик, возможно тебе будет интересно!

Источник

Признаки делимости чисел

В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.

Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.

Примеры:

4, 32, 50, 112, 2174 – последние цифры этих чисел четные, значит они делятся на 2.

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.

Примеры:

18 – делится на 3, т.к. 1+8=9, а число 9 делится на 3 (9:3=3).

Признак делимости на 4

Двузначное число

Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.

• 64 – делится на 4, т.к. 6⋅2+4=16, а 16:4=4.
• 35 – не делится на 4, т.к. 3⋅2+5=11, а .

Число разрядов больше 2

Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.

344 – делится на 4, т.к. 44 кратно 4 (по алгоритму выше: 4⋅2+4=12, 12:4=3).

Примечание:

Число делится на 4 без остатка, если:

• в его последнем разряде стоят цифры 0, 4 или 8, а предпоследний разряд при этом является четным;
• в последнем разряде – 2 или 6, а в предпоследнем – нечетные цифры.

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.

Примеры:

10, 65, 125, 300, 3480 – делятся на 5, т.к. оканчиваются на 0 или 5.

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).

Примеры:

• 486 – делится на 6, т.к. делится на 2 (последняя цифра 6 – четная) и на 3 (4+8+6=18, 18:3=6).
• 712 – не делится на 6, т.к. оно кратно только 2.
• 1345 – не делится на 6, т.к. не является кратным ни 2, ни 3.

Признак делимости на 7

Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.

• 91 – делится на 7, т.к. 9⋅3+1=28, а 28:7=4.
• 105 – делится на 7, т.к. 10⋅3+5=35, а 35:7=5 (в числе 105 – десять десятков).
• 812 – делится на 7. Здесь следующая цепочка: 81⋅3+2=245, 24⋅3+5=77, 7⋅3+7=28, а 28:7=4.
• 302 – не делится на 7, т.к. 30⋅3+2=92, 9⋅3+2=29, а число 29 на 7 не делится.

Признак делимости на 8

Трехзначное число

Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.

• 264 – делится 8, т.к. 2⋅4+6⋅2+4=24, а 24:8=3.
• 716 – не делится 8, т.к. 7⋅4+1⋅2+6=36, а .

Число разрядов больше 3

Число делится на 8, когда три последние цифры образуют число, делящееся на 8.

• 2336 – делится на 8, т.к. 336 кратно 8.
• 12547 – не кратно 8, т.к. 547 не делится без остатка на восемь.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.

Примеры:

• 324 – делится на 9, т.к. 3+2+4=9, а 9:9=1.
• 921 – не делится на 9, т.к. 9+2+1=12, а

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Примеры:

• 10, 110, 1500, 12760 – кратные 10 числа, последняя цифра – 0.
• 53, 117, 1254, 2763 – не делятся на 10.

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.

Примеры:

• 737 – делится на 11, т.к. |(7+7)-3|=11, 11:11=1.
• 1364 – делится на 11, т.к. |(1+6)-(3+4)|=0.
• 24587 – не делится на 11, т.к |(2+5+7)-(4+8)|=2, а 2 не делится на 11.

Источник