Что значит конгруэнтные фигуры

конгруэнтные фигуры

Энциклопедический словарь . 2009 .

Смотреть что такое «конгруэнтные фигуры» в других словарях:

КОНГРУЭНТНЫЕ ФИГУРЫ — (от лат. congruens родительный падеж congruentis соответствующий, совпадающий), геометрические фигуры, переходящие друг в друга при движении … Большой Энциклопедический словарь

КОНГРУЭНТНЫЕ ФИГУРЫ — (от лат congruens, род. п. congruentis соответствующий, совпадающий), геом. фигуры, переходящие друг в друга при движении … Естествознание. Энциклопедический словарь

Площадь фигуры — У этого термина существуют и другие значения, см. Площадь (значения). Площадь плоской фигуры аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное… … Википедия

Равновеликие фигуры — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

РАВНОВЕЛИКИЕ И РАВНОСОСТАВЛЕННЫЕ ФИГУРЫ — две фигуры в R2, имеющие равные площади и соответственно два многоугольника M1 и М 2 такие, что их можно разрезать на многоугольники так, что части, составляющие М 1, соответственно конгруэнтны частям, составляющим М 2. Для , равновеликость… … Математическая энциклопедия

Квадрируемая фигура — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

Квадрируемость — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

Площадь (геометрия) — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

Площадь (в геометрии) — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

Площадь многоугольника — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

Источник

Конгруэнтные фигуры

Конгруэнтные фигуры.

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

§ 4. Конгруэнтные фигуры. А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

П е р в о е о п р е д е л е н и е . Фигура Фх конгруэнтна фигуре
Ф, если существует сохраняющее расстояния отображение
фигуры Ф на Фх.
Так как перемещения сохраняют расстояния, часто употребляется
такой метод доказательства конгруэнтности фигур Ф и Фх:
находится перемещение, при котором образом фигуры Ф является
Фх.
В т о р о е о п р е д е л е н и е . Если существует перемещение,
отображающее фигуру Ф на Фх, то говорят, что фигура Фх конгруэнтна
Ф.
Замечание, сделанное перед этим определением, показывает,
что если фигура Фх конгруэнтна фигуре Ф в смысле второго определения,
то Фх конгруэнтна Фив смысле первого определения.

257 Конгруэнтные фигуры.

Для доказательства эквивалентности этих двух определений
остается показать, что если существует сохраняющее расстояния
отображение G, область определения которого — фигура Ф, а
множество значений — Фх, то существует и перемещение F (изометрическое
отображение всей плоскости, а не ее подмножества Ф),
при котором образ фигуры Ф — фигура Фх.
Т е о р е м а 4.1. Для любого сохраняющего расстояния отображения
G произвольной фигуры Ф в плоскость существует перемещение
F, являющееся продолжением G на всю плоскость (для любой
точки X фигуры Ф имеем: F (X) — G (X)).
Д о к а з а т е л ь с т в о . Если Ф состоит из одной или двух
точек, то утверждение теоремы — очевидное следствие A.IV.1.
Рассмотрим другие возможности.
Первый случай: Ф — подмножество прямой.
Пусть А и В — различные точки Ф. Обозначим через Лх и Вг
образы точек А а В при отображении G. Так как G сохраняет расстояния,
|Лх5х1 = |Л5|. Вследствие А.IV.1. существует перемещение
F, переводящее А в Аъ В в Вх.
Отображения G и F сохраняют расстояния. Значит, G (Ф),
F (Ф) — подмножества прямой Л^. Возьмем отличную от Л и Б
точку Xфигуры Ф. НапрямойЛхбх имеется ровно одна точка Х1г
для которой |ЛХ| = |ЛхХх|, |fiX| =|SxXx|. Поэтому и F, и G
переводят X в X’, т. е. F — продолжение G на всю плоскость.
Второй случай: Ф содержит точки А, В, С, не принадлежащие
одной прямой.
Так как G сохраняет расстояния, точки Ах — G (Л), Вх — G (В),
Сх = G (С) также не принадлежат одной прямой, причем | Лх-SxN
= | АВ\, |ВхСх1 = |ВС|, |ЛхСх1 =|ЛС|. Как показано при доказательстве
теоремы 2.1 существует перемещение F, которое, как и
С, переводит Л в Аг, В в Въ С в Сх. Если Ф не содержит других
точек, кроме Л, б и С, теорема доказана. Пусть X — произвольная
точка Ф, отличная от Л, Б, С.
В этом случае мы докажем, что F (X) = G (X), показав, что существует
не более одной точки плоскости, удаленной от Л’ на расстояние
| ЛХ|, от В’ — на |fiX| и от С’— на |СХ|.
В самом деле, имеется не более двух точек Y1 и Y» плоскости,
для каждой из которых расстояние от Ах равно |ЛХ|, а от Вх —
|£Х| (теорема 1.З.), причем эти точки симметричны относительно
прямой АВ. Но \C’Y’\^ | C’Y»\: если эти расстояния равны, а
Y* ф Y», то С’ — точка меди-
атрисы к отрезку Y’Y», т. е.
С’ € (ЛхВх). Это противоречит
предположению С £ (АВ).
Надо добавить, что хотя приведенные
определения и эквивалентны,
числа, показывающие,
сколько имеется отображений,
устанавливающих конгруэнт

258 Конгруэнтные фигуры.

ность фигуры Ф фигуре Фх в смысле первого и второго определений,
могут оказаться различными. Так, с сохранением расстояний
отрезок на отрезок равной длины отображается двумя способами,
а перемещений, переводящих первый отрезок во второй, существует
четыре.
Так как перемещения плоскости образуют группу, сразу получаем:
У.4.1. Отношение конгруэнтности на множестве фигур является
отношением эквивалентности.
Отношение конгруэнтности фигур обозначается знаком е^.
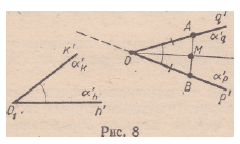
Т е о р е м а 4.2. Для любого луча р’ в заданной полуплоскости
а’ с границей р существует единственный луч q’, имеющий общее
начало с р’, такой, что угол p’q’ конгруэнтен данному углу h’k’.
Д о к а з а т е л ь с т в о . Если в полуплоскости а’ существует
такой луч q’, что Z. p’q’ ^ A.h’k’, то перемещение, отображающее
угол h’k’ на угол p’q’, переводит Ох в О (рис. 8), а луч h’ ,(или k’)
отображается на луч р’\ при этом полуплоскость ah, содержащая k’
(соответственно полуплоскость а*, содержащая Н’), отображается
на а’р. как уже говорилось выше, при перемещениях крайние (граничные)
точки множества отображаются на крайние (граничные)
точки его образа. Таких перемещений в силу A.IV.2 имеется два.
Обозначим их через Ft и F%. Тогда
FAh’)=p’\ f!«)=«;,
F2 (kr) = p’, F2 (a’) = a’.
Fi (k1) и F
g (p’) — искомые лучи. Теорема существования доказана.
Для доказательства единственности остается показать, что
Fy (k’) = F2 (h’). Обозначим через q’ луч Ft (k’). Возьмем на лучах
р’ и q’ точки А и В: \ОА \ = \0В\.
Симметрия относительно медиатрисы ОМ отрезка АВ переводит
р’ в q’, q’ в р’у а полуплоскость а’р, содержащую^ q\ — в полуплоскость
a’q, содержащую р’.
Рассмотрим перемещение Som ° Ft. Имеем:
Som о Fi (&’) = S0M (qr) = p’.
s om o F ,K) = sM(«;) = a;.
Итак, образы флага 0$a’k при перемещениях F2 и Som ° FL
совпадают. В силу единственности перемещения, отображающего
один из данных флагов на другой, Som ° Fx = F2. Так как F2 (h’) =
= (So.m 0 Fj) (h’) = Som (p ) = q’, теорема доказана.
Т е о р е м а 4.3. Если треугольники АуВ^Су и А2В.,С2 таковы,
что BiAjCi ^ Z. В2А2С2, \AiBi\ = \А2В2\, \AiCi\== 1Л2С2!, то
АА2В2С2 ^ ААхВхСх.
Д о к а з а т е л ь с т в о . Так как Z-B^Cx ^ Z.B.2A2C2, существует
перемещение F, отображающее Ах на А2, луч АгВх на луч

259 Конгруэнтные фигуры.

А2Въ а луч Afix на луч Л2С2. Воспользовавшись условиями
\AxBx| = | Л2В2|, \AxCx| = 1Л2С21 и единственностью точки луча,
удаленной от его начала на данное расстояние, получаем, что
Аналогично доказываются другие признаки конгруэнтности
треугольников: по трем сторонам, по стороне и двум прилежащим
к ней углам.
О п р е д е л е н и е . Угол, конгруэнтный своему смежному, называется
прямым углом.
Для выпуклого угла имеются два угла, смежные с ним (рис. 9).
Поэтому вначале необходимо доказать корректность этого определения:
если Z.lg^Z.2, то Z . l ^ Z . 3 (рис. 9).
Угол 2 при симметрии Sa отображается на конгруэнтный ему
угол. Но луч ОА при симметрии Sa отображается на себя и по условию
Z. 1 Z. 2. Так как по теореме 4.2 от луча О А можно отложить
в данной полуплоскости лишь один угол, конгруэнтный данному,
$а _____
то [ОБ) ==> [ОС). Следовательно, и прямая р при симметрии Sa
отображается на’себя.
Из теоремы 3.4 вытекает, что Sp (а) — а. Поэтому угол 1 при
симметрии Sp отображается на угол 3, т. е. Z. 1 Ш АЗ.
Если две прямые пересекаются, то, как известно, они задают
четыре выпуклых угла. Из доказанной корректности определения
прямого угла следует, что если один из этих четырех углов прямой,
то и все четыре угла прямые.
О п р е д е л е н и е . Дее прямые, образующие при пересечении
прямые углы, называются взаимно перпендикулярными.
Т е о р е м а 4.4. Для любой точки О плоскости и любой прямой
р существует одна и только одна прямая, проходящая через О
и перпендикулярная р.
Д о к а з а т е л ь с т в о . Рассмотрим два случая.
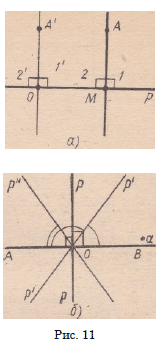
Первый случай’. О $ р.
а) С у щ е с т в о в а н и е . Пусть О* = Sp (О) и М — точка
пересечения прямых 00′ и р (рис. 10, а). При еимметрии Sp лучи
МО и МО’ отображаются друг на друга, луч MN — на себя. Поэтому
углы OMN и O’MN — смежные и конгруэнтные углы. Это
означает, что прямые 00′ и р перпендикулярны.
б) Е д и н с т в е н н о с т ь . Допустим, что через точку О

260 Конгруэнтные фигуры.

проходят два перпендикуляра к прямой
р (рис. 11,6). Тогда, как это следует из
теоремы 4.2, прямые О А и О В при симметрии
Sp отображаются на себя. Так как эти
прямые пересекаются в точке О, отсюда получаем,
что эти прямые имеют вторую общую
точку O’— Sp (О). Но через две точки
проходит единственная прямая, поэтому
(ОА) = (ОВ). Это противоречит сделанному
допущению.

Конгруэнтные фигуры 2

Второй случай1. О £ р.
а) С у щ е с т в о в а н и е . Возьмем
произвольную точку A tp. Как мы только
что показали, существует прямая AM (М £
;
няя точка) развернутого угла не единственна.

Источник

Конгруэнтность (геометрия) — Congruence (geometry)

В геометрии две фигуры или объекты являются конгруэнтными, если они имеют одинаковую форму и размер, или если один имеет такую ​​же форму и размер, что и зеркальное отображение другого.

Более формально, два набора точек называются конгруэнтными, если и только если одна может быть преобразована в другую с помощью изометрии , т. Е. Комбинации жестких движений , а именно сдвига , вращения и отражения . Это означает, что любой объект можно перемещать и отражать (но не изменять размер) так, чтобы он точно совпадал с другим объектом. Таким образом, две отдельные плоские фигуры на листе бумаги являются конгруэнтными, если мы можем вырезать их, а затем полностью сопоставить. Переворачивание бумаги разрешено.

В элементарной геометрии слово конгруэнтное часто используется следующим образом. Слово равно часто используется вместо конгруэнтного для этих объектов.

• Два отрезка совпадают, если они имеют одинаковую длину.
• Два угла равны, если имеют одинаковую меру.
• Два круга конгруэнтны, если имеют одинаковый диаметр.

В этом смысле конгруэнтность двух плоских фигур подразумевает, что их соответствующие характеристики «совпадают» или «равны», включая не только их соответствующие стороны и углы, но также их соответствующие диагонали, периметры и площади.

Связанная концепция подобия применяется, если объекты имеют одинаковую форму, но не обязательно имеют одинаковый размер. (Большинство определений рассматривают конгруэнтность как форму подобия, хотя меньшинство требует, чтобы объекты имели разные размеры, чтобы считаться подобными.)

СОДЕРЖАНИЕ

Определение конгруэнтности многоугольников

Чтобы два многоугольника были конгруэнтными, они должны иметь равное количество сторон (и, следовательно, равное количество — то же количество — вершин). Два многоугольника с n сторонами конгруэнтны тогда и только тогда, когда каждый из них имеет численно идентичные последовательности (даже если по часовой стрелке для одного многоугольника и против часовой стрелки для другого) сторона-угол-сторона-угол -. для n сторон и n углов.

Конгруэнтность многоугольников можно установить графически следующим образом:

• Сначала сопоставьте и пометьте соответствующие вершины двух фигур.
• Во-вторых, нарисуйте вектор от одной из вершин одной из фигур к соответствующей вершине другой фигуры. Переведите первую фигуру по этому вектору так, чтобы эти две вершины совпали.
• В-третьих, поверните переведенную фигуру вокруг совпадающей вершины, пока одна пара соответствующих сторон не совпадет.
• В-четвертых, отразите повернутую фигуру на этой совпадающей стороне, пока фигуры не совпадут.

Если в какой-то момент шаг не может быть завершен, полигоны не совпадают.

Конгруэнтность треугольников

Два треугольника конгруэнтны, если их соответствующие стороны равны по длине, а соответствующие им углы равны по мере.

Если треугольник ABC конгруэнтен треугольнику DEF, математически это соотношение можно записать как:

△ А B C ≅ △ D E F . <\ Displaystyle \ треугольник \ mathrm \ cong \ треугольник \ mathrm .>

Во многих случаях достаточно установить равенство трех соответствующих частей и использовать один из следующих результатов, чтобы вывести конгруэнтность двух треугольников.

Определение конгруэнтности

Достаточные доказательства соответствия между двумя треугольниками в евклидовом пространстве могут быть представлены с помощью следующих сравнений:

• SAS (сторона-угол-сторона): если две пары сторон двух треугольников равны по длине, а прилегающие углы равны при измерении, то треугольники совпадают.
• SSS (сторона-сторона-сторона): Если три пары сторон двух треугольников равны по длине, то треугольники равны.
• ASA (угол-сторона-угол): если две пары углов двух треугольников равны по размеру, а включенные стороны равны по длине, то треугольники конгруэнтны.

Постулат ASA был внесен Фалесом Милетским (греч.). В большинстве систем аксиом три критерия — SAS, SSS и ASA — устанавливаются в виде теорем . В школьной группе по математике система SAS рассматривается как один (№ 15) из 22 постулатов.

• AAS (угол-угол-сторона): если две пары углов двух треугольников равны по размеру, и пара соответствующих не включенных сторон равны по длине, то треугольники конгруэнтны. AAS эквивалентен условию ASA тем фактом, что если заданы любые два угла, то же самое и третий угол, поскольку их сумма должна составлять 180 °. ASA и AAS иногда объединяют в одно условие, AAcorrS — любые два угла и соответствующую сторону.
• RHS (right-angle-hypotenuse-side), также известный как HL (hypotenuse-leg): если два прямоугольных треугольника имеют гипотенузы одинаковой длины, а пара более коротких сторон равны по длине, то треугольники конгруэнтны. .

Боковой угол

Условие SSA (сторона-сторона-угол), которое определяет две стороны и невключенный угол (также известный как ASS, или угол-сторона-сторона), само по себе не доказывает совпадения. Чтобы показать соответствие, требуется дополнительная информация, такая как измерение соответствующих углов и, в некоторых случаях, длины двух пар соответствующих сторон. Есть несколько возможных случаев:

Если два треугольника удовлетворяют условию SSA и длина стороны, противоположной углу, больше или равна длине соседней стороны (SSA, или длинная сторона-короткий боковой угол), то эти два треугольника совпадают. Противоположная сторона иногда длиннее, если соответствующие углы острые, но всегда длиннее, когда соответствующие углы прямые или тупые. Если угол является прямым углом, также известным как постулат гипотенузы (HL) или условие прямоугольной стороны гипотенузы (RHS), третья сторона может быть вычислена с использованием теоремы Пифагора, что позволяет вычислить постулат SSS. применяемый.

Если два треугольника удовлетворяют условию SSA и соответствующие углы являются острыми, а длина стороны, противоположной углу, равна длине смежной стороны, умноженной на синус угла, то два треугольника конгруэнтны.

Если два треугольника удовлетворяют условию SSA и соответствующие углы являются острыми, а длина стороны, противоположной углу, больше, чем длина смежной стороны, умноженная на синус угла (но меньше длины соседней стороны), тогда нельзя показать, что два треугольника совпадают. Это неоднозначный случай, и из данной информации могут быть образованы два разных треугольника, но дополнительная информация, позволяющая их различать, может привести к доказательству соответствия.

Угол-угол-угол

В евклидовой геометрии AAA (угол-угол-угол) (или просто AA, поскольку в евклидовой геометрии углы треугольника в сумме составляют 180 °) не дает информации о размере двух треугольников и, следовательно, доказывает только сходство, а не конгруэнтность в евклидовом пространстве.

Однако в сферической геометрии и гиперболической геометрии (где сумма углов треугольника зависит от размера) AAA достаточно для сравнения на заданной кривизне поверхности.

CPCTC

Этот акроним означает « Соответствующие части конгруэнтных треугольников являются конгруэнтными» , сокращенная версия определения конгруэнтных треугольников.

Более подробно, это сжатый способ сказать, что если треугольники ABC и DEF совпадают, то есть

△ А B C ≅ △ D E F , <\ Displaystyle \ треугольник ABC \ cong \ треугольник DEF,>

с соответствующими парами углов в вершинах A и D ; B и E ; и C и F , и с соответствующими парами сторон AB и DE ; BC и EF ; и CA и FD , то верны следующие утверждения:

А B ¯ ≅ D E ¯ <\ Displaystyle <\ overline > \ cong <\ overline >> B C ¯ ≅ E F ¯ <\ Displaystyle <\ overline > \ cong <\ overline >> А C ¯ ≅ D F ¯ <\ Displaystyle <\ overline > \ cong <\ overline >> ∠ B А C ≅ ∠ E D F <\ Displaystyle \ угол ВАС \ конг \ угол EDF> ∠ А B C ≅ ∠ D E F <\ Displaystyle \ угол ABC \ cong \ angle DEF> ∠ B C А ≅ ∠ E F D . <\ Displaystyle \ angle BCA \ cong \ angle EFD.>

Утверждение часто используется в качестве обоснования в доказательствах элементарной геометрии, когда требуется заключение о конгруэнтности частей двух треугольников после того, как конгруэнтность треугольников была установлена. Например, если два треугольника были показаны как совпадающие по критериям SSS, и утверждение, что соответствующие углы совпадают, необходимо в доказательстве, то CPCTC может использоваться в качестве обоснования этого утверждения.

Связанная теорема — CPCFC , в которой «треугольники» заменены «фигурами», так что теорема применима к любой паре многоугольников или многогранников , которые конгруэнтны.

Определение сравнения в аналитической геометрии

В евклидовой системе конгруэнтность фундаментальна; это аналог равенства для чисел. В аналитической геометрии конгруэнтность может быть определена интуитивно следующим образом: два отображения фигур в одну декартову систему координат совпадают тогда и только тогда, когда для любых двух точек в первом отображении евклидово расстояние между ними равно евклидову расстоянию между соответствующими точки во втором отображении.

А государства более формальное определения , что два подмножества A и B из евклидова пространства R п называется конгруэнтным , если существует изометрия п : R п → R н (элемент из евклидовой группы Е ( п )) с F ( A ) = B . Конгруэнтность — это отношение эквивалентности .

Конгруэнтные конические сечения

Два конических сечения конгруэнтны, если их эксцентриситет и один другой отдельный параметр, их характеризующий, равны. Их эксцентриситет определяет их формы, равенства которых достаточно для установления сходства, а второй параметр затем устанавливает размер. Поскольку две окружности , параболы или прямоугольные гиперболы всегда имеют одинаковый эксцентриситет (в частности, 0 в случае окружностей, 1 в случае парабол и в случае прямоугольных гипербол), две окружности, параболы или прямоугольные гиперболы должны иметь одинаковый эксцентриситет. только одно другое общее значение параметра, определяющее их размер, чтобы они были конгруэнтными. 2 <\ displaystyle <\ sqrt <2>>>

Конгруэнтные многогранники

Для двух многогранников с одинаковым комбинаторным типом (то есть с одинаковым количеством ребер E , одинаковым количеством граней и одинаковым количеством сторон на соответствующих гранях) существует набор измерений E, которые могут установить, является ли многогранники конгруэнтны. Число является точным, что означает, что измерений меньше E недостаточно, если многогранники являются общими для своего комбинаторного типа. Но для особых случаев можно использовать меньшее количество измерений. Например, у куба 12 ребер, но 9 измерений достаточно, чтобы решить, конгруэнтен ли многогранник этого комбинаторного типа данному правильному кубу.

Конгруэнтные треугольники на сфере

Как и в случае плоских треугольников, на сфере два треугольника, разделяющие одну и ту же последовательность угол-сторона-угол (ASA), обязательно конгруэнтны (то есть, у них есть три одинаковые стороны и три одинаковых угла). Это можно увидеть следующим образом: можно расположить одну из вершин с заданным углом на южном полюсе и пройти стороной с заданной длиной вверх по нулевому меридиану. Знание обоих углов на обоих концах сегмента фиксированной длины гарантирует, что две другие стороны исходят с однозначно определенной траекторией и, таким образом, встретятся друг с другом в однозначно определенной точке; таким образом, ASA действительна.

Теоремы сравнения сторона-угол-сторона (SAS) и сторона-сторона-сторона (SSS) также верны для сферы; кроме того, если два сферических треугольника имеют одинаковую последовательность угол-угол-угол (AAA), они конгруэнтны (в отличие от плоских треугольников).

Теорема сравнения плоскость-треугольник, угол-угол-сторона (AAS) не верна для сферических треугольников. Как и в случае с плоской геометрией, боковой-боковой угол (SSA) не подразумевает конгруэнтности.

Обозначение

Обычно для сравнения используется символ равенства с тильдой над ним, ≅ , соответствующий символу Unicode «приблизительно равно» (U + 2245). В Великобритании иногда используется трехстрочный знак равенства ≡ (U + 2261).

Источник