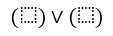- Что значит количество логических переменных
- Таблица истинности
- Что такое таблицы истинности
- Логические операции
- Логические выражения
- Конъюнкция
- Дизъюнкция
- Правила составления таблицы истинности
- Примеры построения таблицы истинности
- Логические выражения и таблица истинности
- Логические выражения и таблица истинности
- Построение таблиц истинности
- Алгоритм построения таблицы истинности логической функции
- Готовые работы на аналогичную тему
- Алгоритм построения логической функции по ее таблице истинности
Что значит количество логических переменных

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Логическая функция — это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части — соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций.
Порядок выполнения логических операций в сложном логическом выражении:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений:
- Определить количество строк:
количество строк = 2 n + строка для заголовка,
n — количество простых высказываний.
Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
- определить количество переменных (простых выражений);
- определить количество логических операций и последовательность их выполнения.
Пример: Составить таблицу истинности логического выражения:
Решение: Ù
- Определить количество строк:
Источник
Таблица истинности
Что такое таблицы истинности
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.
Таблица истинности необходима для совершения логических операций. Она включает в себя n+1 столбцы и 2 n строки, где n — число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов.
Набором называется совокупность значений переменных. А = 0, В = 1. В случае, когда количество переменных n, число различных наборов будет равно 2 N . Например, для трех переменных число разных наборов будет равно 2 3 = 8.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).
Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.
Логические операции
Логические операции — построение из одного или нескольких высказываний нового высказывания.
Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.
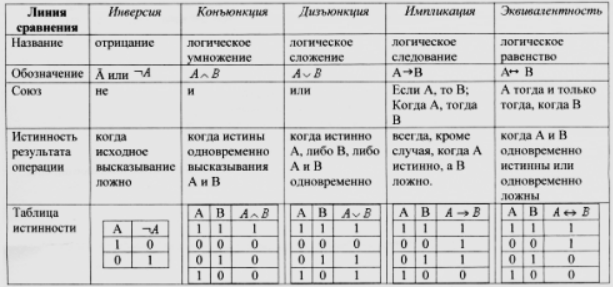
К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.
Логические выражения
Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».
Их можно разделить на два типа:
- выражения, использующие операции сравнения и принимающие логические значения. Например, выражение a Определение
Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.
Унарной в данном случае называется операция, которая используется относительно одной величины.
Конъюнкция
Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧.
Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.
Дизъюнкция
Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.
Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.
Правила составления таблицы истинности
Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.
Строить таблицы истинности необходимо по следующему алгоритму:
- Вычислить число переменных в выражении (n).
- Вычислить общее количество логических операций в выражении.
- Определить последовательность, в которой будут выполняться логические операции.
- Установить количество столбцов в таблице — количество переменных и количество операций.
- Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3.
- Высчитать количество строк в таблице, используя формулу m = 2 n
- Занести в таблицу наборы входных переменных. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2 n −1.
- Заполнить таблицу, совершая логические операции.
Примеры построения таблицы истинности
Задача
Построим таблицу истинности и решим выражение \( F = (A \vee B) \wedge (¬A \vee ¬B)\) . Будем пользоваться приведенным выше алгоритмом.
- Число переменных в выражении n = 2.
- Общее количество логических операций в выражении — 5.
- Последовательность выполнения логических операций — 1, 5, 2, 4, 3.
- Количество столбцов — 7. Логические переменные (А и В) + логические операции \(\vee\) , \(\wedge\) , \(¬\) , \(\vee\) , \(¬\) = 2 +5 = 7.
- Количество строк — 5, исходя из m =2 n , таким образом 2 2 = 4, 4+1 (строка заголовков столбцов) = 5.
- Заполним таблицу.
Решение
| А | В | \(А \vee В\) | ¬А | ¬В | \(¬А \vee ¬В\) | \((A \vee B) \wedge (¬A \vee ¬B)\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0 при A = B = 0 и A = B = 1
Задача
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)
- Число переменных в выражении n = 3.
- Общее количество логических операций в выражении — 3.
- Последовательность выполнения логических операций — 3, 2, 1.
- Количество столбцов — 6. Логические переменные (X, Y, Z) + логические операции \( \vee\) , \(\wedge\) , ¬ = 3 + 3 = 6.
- Количество строк — 9, исходя из m =2 n , таким образом 2 3 = 8, 8+1 (строка заголовков столбцов) = 9.
- Заполним таблицу.
Решение
| X | Y | Z | ¬ Z | \(Y \wedge ¬Z\) | \(X \vee Y \wedge ¬Z\) |
| 0 | 0 | 0 | q | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1.
Источник
Логические выражения и таблица истинности
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2 n , где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
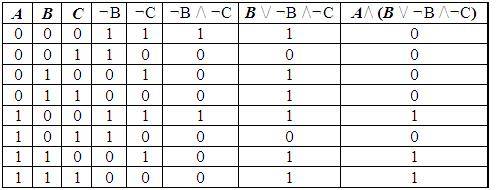
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2 n , m=2 2 =4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
Источник
Построение таблиц истинности
Вы будете перенаправлены на Автор24
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
Готовые работы на аналогичную тему
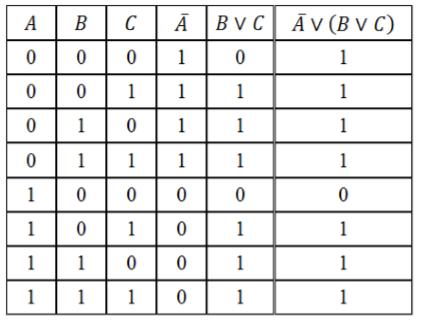
Составить таблицу истинности логического выражения $D=\bar \vee (B \vee C)$.
Решение:
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
Кол-во столбцов = $3 + 3=6$.
Заполним таблицу, учитывая таблицы истинности логических операций.
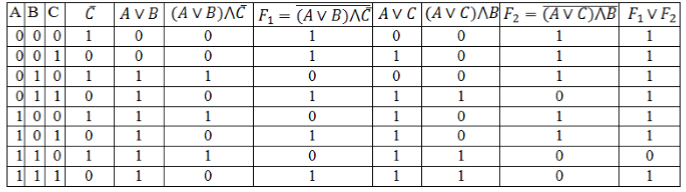
По данному логическому выражению построить таблицу истинности:
Решение:
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($\bar
$); - дизъюнкция, т.к. она находится в скобках ($A \vee B$);
- конъюнкция ($(A\vee B)\bigwedge \overline
$); - отрицание, которое обозначим $F_1$ ($\overline<(A\vee B)\bigwedge \overline
>$); - дизъюнкция ($A \vee C$);
- конъюнкция ($(A\vee C)\bigwedge B$);
- отрицание, которое обозначим $F_2$ ($\overline<(A\vee C)\bigwedge B>$);
Кол-во столбцов = $3 + 8 = 11$.
Заполним таблицу, учитывая таблицу истинности логических операций.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
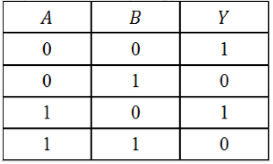
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 12 04 2016
Источник