Что значит кодирование чисел

Кодирование числовой информации

Введение

Если у вас возникли какие-либо вопросы при изучении темы «Кодирование числовой информации», то звоните мне и записывайтесь на первый репетиторский урок по информатике и ИКТ. На моих индивидуальных уроках мы с вами закроем текущие пробелы в ваших знаниях и прорешаем колоссальное количество всевозможных тематических упражнений.

Общие понятие о числовой информации

Думаю, что превалирующее число школьников и студентов знает фразу: «Математика – царица всех наук!». А как известно, математика очень интенсивно оперирует числами, цифрами и действиями над числами.

Первый счет появился много тысячелетий назад, так как даже в очень древние времена люди столкнулись с потребностью в счете. Его возникновение связано с желанием человека проинформировать своих соплеменников о количестве обнаруженных им объектов, предметов. По началу люди просто делили предметы по принципу один-много. То есть не было обозначения для двух, трех, десяти и более различных предметов. Их просто обозначали в количественном отношении как много.

Постепенно люди научились подключать к арифметическому счету пальцы на своих руках. С их помощью можно было считать до пяти, а если использовать обе руки, то до десяти различных предметов. Именно десятичная система счисления получило свое развитие на основе использования при счете пальцев рук.

Вернемся в настоящий временной континуум. Для современного человека знания, позволяющие считать предметы и записывать числа, являются обязательными. Арифметика изучается в школе с первого класса. Цифры, используя которые мы записываем числа, называются арабскими. Алфавит арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего десять различных цифр или состояний.

Числа можно классифицировать на две фундаментальные группы:

Дробные или действительные числа.

Каждое число из представленных групп может быть либо:

Примеры различных десятичных чисел:

-56 — целое отрицательное число;

12.78 — действительное положительное число;

0.0 — действительное число, равное нулю;

12000 — целое положительное число.

Наша цель – понять, каким образом производится кодирование числовой информации, выраженной целыми или дробными числами, которые являются положительными, отрицательными или равными нулю. Другими словами, мы должны понять, как персональный компьютер хранит, обрабатывает, копирует числа на «своем» уровне.

Свойства числовой информации

Конечность. Информация, выраженная числовым значением, должна быть конечной. Процессор персонального компьютера не сможет обработать число, которое не является конечным или завершенным. То есть прежде чем приступить к кодированию числовой информации, процессор должен быть уверен, что данное значение записано полностью и не будет изменено пользователем.

Понятность. Если мы говорим о кодировании числовой информации, которая представлена десятичным числом, то необходимо, чтобы само число состояло из элементов, которые будут понятны исполнителю при кодировании. Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.

Приведенные два свойства являются ключевыми в алгоритмах кодирования числовой информации. Пожалуй, еще стоит отметить неосновное свойство – размер числа. Но в современном мире мощности персональных компьютеров постоянно увеличиваются и самые эффективные процессоры способы обрабатывать огромные значения.

Способы кодирования числовой информации

Сразу необходимо твердо уяснить следующее: процессор персонального компьютера взаимодействует с любыми данными исключительно на уровне цепочек, состоящих из 0 и 1. Набор нулей и единиц называют двоичным или бинарным кодом. То есть любые текстовые, символьные или числовые значения, которые понятны простому человеку, процессор преобразует в двоичный код. Следовательно, наша задача – научиться переводить числовые значения в бинарное представление, состоящее из цепочек 0 и 1.

Для полного осознания алгоритма кодирования числовой информации необходимо очень хорошо уяснить понятие «Машинное слово». Возможно вы слышали, что иногда пользователи говорят, что на их компьютерах установлена 32-х разрядная или 64-х разрядная система Microsoft Windows. Именно значение разрядности (в приведенном примере это 32 или 64) и отвечает за то, сколько бит информации будет выделено для хранения какого-либо математического значения при кодировании числовой информации. То есть, если нам дано положительное целое число 25, то при преобразовании его в бинарный код, ему будет выделено 32 или 64 бита. Также напомню, что один байт информации состоит из 8 битов.

Далее по тексту я буду работать на уровне 16-и разрядной системы. То есть любое кодирование числовой информации будет представлено с использованием машинного слова в 16 бит.

Кодирование целых положительных чисел

Это наиболее простой способ кодирования данных, так как для его реализации необходимо уметь переводить числа из десятичной системы счисления в двоичную систему. Ниже я приведу таблицу, в которой покажу кодирование целых положительных чисел различной значности.

Исходное десятичное число

Закодированное десятичное число в двоичном коде

Источник

Кодирование числовой информации

Вы будете перенаправлены на Автор24

Десятичное и двоичное представление чисел

Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: от $0$ до $9$. Эта система называется десятичной.

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры — логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).

Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.

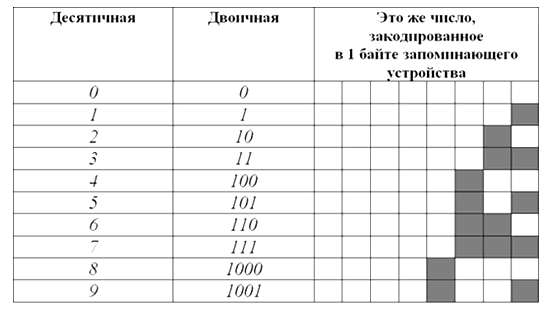
Вот таблица первых десяти чисел в каждой из этих систем счисления:

Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.

Готовые работы на аналогичную тему

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта). Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус — необходимость иметь дело с большим количеством разрядов.

Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы — $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.

Алгоритмы кодирования чисел в двоичной системе счисления

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

Небольшие целые числа без знака.

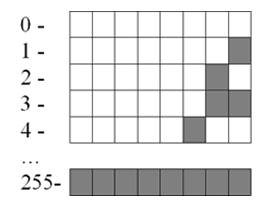
Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

Большие целые числа и числа со знаком.

Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).

Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком «плюс», этот бит остается пустым, если со знаком «минус» – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах. Например, алгоритм кодирования числа $+2676$ будет следующим:

• Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
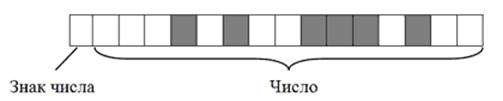
• Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.

В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:

Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:

1. Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
2. Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
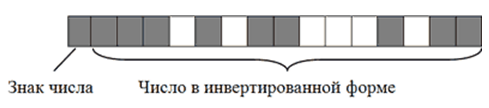
3. Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:

Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).

Дробные числа со знаком.

Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):

• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком «плюс» – бит остается пустым.
• во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
• в следующих за ним $7$ битах записывается значение порядка.
• в оставшихся $23$ битах записывается так называемая мантисса числа.

Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.

Порядок кодирования будет примерно следующим:

1. Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
2. Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
3. Определить значение и знак порядка. Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);

Знак порядка – это направление, в котором пришлось двигать запятую: влево – «плюс», вправо – «минус». В нашем примере запятая двигалась влево, поэтому знак порядка – «плюс».

Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается. Числа с плавающей запятой, кодируемые в $32$ битах, называю числами одинарной точности. Когда для записи числа $32$-битной ячейки недостаточно, компьютер может использовать ячейку из $64$ битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.

Источник

Что значит кодирование чисел

Числа, записанные в разных системах счисления, принципиально ничем не отличаются друг от друга. Значение числа двадцать восемь, обозначающего количество школьников в классе, не изменяется в случае его записи в двоичной, троичной или восьмеричной системах счисления. В этом случае оно записывается с помощью других символов – цифр, но по-прежнему означает то же самое количество школьников. Люди с дества умеют выполнять арифметические операции с числами, записываемыми в десятичной системе счисления. Числа можно складывать и умножать, вычитать и делить, производить такие операции столбиком на листе бумаги, в уме или с использованием калькулятора. Аналогично такие же действия можно производить и с числами, записанными в других системах счисления.

Выполнение арифметических действий с двоичными числами можно рассмотреть на примере операции сложения. Такой выбор обусловлен и тем, что компьютер, работая с двоичными числами, заменяет все арифметические действия операцией сложения. Так, например операция вычитания заменяется операцией сложения с отрицательным числом: А–В= А + (–В). Операция умножения заменяется последовательным сложением, а операция деления выполняется через последовательное умножение и вычитание.

Так же, как и для чисел десятичной системы счисления, сложение многозначных двоичных чисел можно выполнить столбиком, записав разряды одного числа под соответствующими разрядами другого числа. Заметим, что роль десятичной «девятки», как самой старшей цифры, в двоичной системе счисления выполняет цифра 1. Поэтому, если при сложении чисел сумма окажется больше 1, то необходимо перенести единицу в соседний старший разряд.

Приведем пример рассуждений, выполняемых при сложении многозначных чисел в двоичной системе счисления.

• ПРИМЕР 1. Найти сумму двоичных чисел 101₂ + 11₂.
• Решение. Запишем разряды одного числа под соответствующими разрядами другого числа.

1)Начинаем выполнять сложение с самого младшего разряда. Согласно таблице сложения двоичных чисел, 1+1=10. Поэтому ноль пишем в младшем разряде, а единица переходит в соседний старший разряд. Эту единицу отмечаем точкой под чертой в соответствующем разряде.

П р о в е р к а.

Проверка подтвердила правильность полученного результата.

Для автоматизации информационных процессов в памяти различных технических устройств необходимо хранить числовые данные. В связи с этим приведение всех хранимых чисел к двоичному виду с учетом только лишь правил перевода из одной системы счисления в другую оказывается недостаточным. При кодировании чисел необходимо учитывать вид чисел (например, целые) и отводимые для их хранения количества ячеек (байтов) памяти компьютера. Чем больше байтов памяти отводится для хранения числа, тем шире множество чисел, одно из которых может быть сохранено.

Один байт памяти содержит 8 битов и хранит последовательность, состоящую из 8 нулей и единиц. Хранимые в байте памяти нули и единицы нужно рассматривать в качестве цифр двоичного 8-разрядного числа и применять к нему различные правила кодирования чисел.

Очевидно, что восемь двоичных нулей соответствует десятичному числу 0 (00000000₂=0₁₀), а восемь двоичных единиц соответствует десятичному числу 255 (11111111₂=255₁₀). При таком кодировании любые сочетания восьми нулей и единиц будут соответствовать десятичным числам от 0 до 255. Все эти числа неотрицательные, и поэтому их записывают без знака. Значит в одном байте памяти (8бит) можно хранить одно из 256 чисел (2 8 =256).

Во многих случаях целых неотрицательных чисел, ограниченных числом 255, оказывается достаточно для решения задач с использованием компьютерной техники. Числа из этого диапазона могут использоваться для обозначения роста и возраста человека, даты и времени, кодов символов и цветов в компьютере.

• ПРИМЕР 2. Закодировать десятичное число 25 для хранения в байте памяти.
• Решение. Число 25 неотрицательное и находится в диапазоне от 0 до 255. К нему может быть применено правило беззнакового кодирования чисел.

1)Переведем десятичное число 25 в двоичную систему счисления.

2)Пронумеруем биты в байте памяти справа налево от 0 до 7.

Источник