Что значит классификация чисел

Классификация действительных чисел

Основной классификация действительных чисел Он делится на натуральные числа, целые числа, рациональные числа и иррациональные числа. Действительные числа обозначены буквой R.

Существует множество способов построения или описания различных действительных чисел — от простых до более сложных, в зависимости от математической работы, которую вы хотите выполнить..

Как классифицируются действительные числа??

Натуральные числа

Это числа, которые используются для подсчета, например, «в стекле четыре цветка».

Некоторые определения начинают натуральные числа с 0, в то время как другие определения начинаются с 1. Для подсчета используются натуральные числа: 1,2,3,4,5,6,7,8,9,10 . и т. Д .; они используются как порядковые или кардинальные числа.

Натуральные числа — это базы, на основе которых можно построить множество других наборов чисел: целые числа, рациональные числа, действительные числа и комплексные числа среди других..

Эти цепочки расширений составляют натуральные числа, канонически идентифицированные в других системах счисления..

Свойства натуральных чисел, такие как делимость и распределение первичных чисел, изучаются в теории чисел.

Проблемы, связанные с подсчетом и упорядочением, такие как перечисления и разбиения, изучаются в комбинаторном.

На обычном языке, как и в начальных школах, натуральные числа можно назвать счетными числами, чтобы исключить отрицательные целые числа и ноль..

У них есть несколько свойств, таких как: сложение, умножение, вычитание, деление и т. Д..

Целые числа

Целые числа — это те числа, которые можно записать без дробной составляющей. Например: 21, 4, 0, -76 и т. Д. С другой стороны, числа типа 8.58 или √2 не являются целыми числами.

Можно сказать, что целые числа являются полными числами вместе с отрицательными числами натуральных чисел. Они используются, чтобы выразить причитающиеся деньги, глубины относительно уровня моря или отрицательную температуру, чтобы назвать несколько применений.

Набор целых чисел состоит из нуля (0), натуральных положительных чисел (1,2,3 . ) и отрицательных целых чисел (-1, -2, -3 . ). Обычно это называется ZZ или жирным шрифтом Z (Z).

Z является подмножеством группы рациональных чисел Q, которые, в свою очередь, образуют группу действительных чисел R. Как и натуральные числа, Z является бесконечной группой учета.

Целые числа образуют наименьшую группу и наименьший набор натуральных чисел. В теории алгебраических чисел целые числа иногда называют иррациональными целыми, чтобы отличать их от алгебраических целых чисел..

Рациональные числа

Рациональное число — это любое число, которое может быть выражено как компонент или дробь двух целых чисел p / q, числителя p и знаменателя q. Поскольку q может быть равно 1, каждое целое число является рациональным числом.

Множество рациональных чисел, часто называемых «рациональными», обозначается через Q.

Десятичное разложение рационального числа всегда заканчивается после конечного числа цифр или когда одна и та же конечная последовательность цифр повторяется снова и снова.

Кроме того, любое повторное или конечное десятичное число представляет собой рациональное число. Эти утверждения верны не только для базы 10, но и для любой другой базы целых чисел.

Вещественное число, которое не рационально, называется иррациональным. Иррациональные числа включают √2, a π и e, например. Поскольку весь набор пригодных для вычисления чисел является счетным, а группа действительных чисел не счетной, можно сказать, что почти все действительные числа иррациональны.

Рациональные числа могут быть формально определены как классы эквивалентностей пар целых чисел (p, q), так что q ≠ 0 или эквивалентное отношение, определенное (p1, q1) (p2, q2), только если p1, q2 = p2q1.

Рациональные числа вместе с сложением и умножением образуют поля, которые составляют целые числа и содержатся в любой ветви, содержащей целые числа..

Иррациональные числа

Иррациональные числа — это все действительные числа, которые не являются рациональными числами; Иррациональные числа не могут быть выражены в виде дробей. Рациональные числа — это числа, состоящие из долей целых чисел..

Как следствие доказательства Кантора, что все действительные числа неисчислимы и что рациональные числа исчисляются, можно сделать вывод, что почти все действительные числа иррациональны.

Когда радиус длины двух отрезков линии является иррациональным числом, можно сказать, что эти отрезки линии несоизмеримы; это означает, что не существует достаточной длины, чтобы каждый из них мог быть «измерен» с определенным кратным целым числом.

К числу иррациональных чисел относятся радиус π от окружности круга до его диаметра, число Эйлера (e), золотое число (φ) и квадратный корень из двух; Более того, все квадратные корни натуральных чисел иррациональны. Единственным исключением из этого правила являются идеальные квадраты.

Можно видеть, что когда иррациональные числа выражаются позиционно в системе счисления (например, в десятичных числах), они не заканчиваются и не повторяются.

Это означает, что они не содержат последовательность цифр, повторение, с помощью которого производится линия представления.

Например: десятичное представление числа π начинается с 3.14159265358979, но не существует конечного числа цифр, которые могут точно представлять π, и при этом они не могут повторяться.

Доказательство того, что десятичное расширение рационального числа должно заканчиваться или повторяться, отличается от доказательства того, что десятичное расширение должно быть рациональным числом; хотя эти тесты являются базовыми и довольно длинными, они требуют некоторой работы.

Обычно математики, как правило, не используют понятие «окончание или повторение» для определения понятия рационального числа..

Иррациональные числа также могут быть обработаны через непрерывные дроби.

Источник

Разряды и классы чисел

Классы чисел

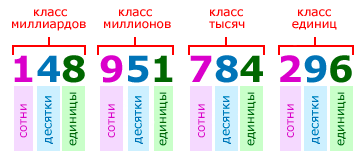
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:

Названия классов многозначных чисел справа налево:

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:

148 951 784 296

и прочитаем число единиц каждого класса слева направо:

148 миллиардов 951 миллион 784 тысячи 296.

При чтении класса единиц в конце обычно не добавляют слово единиц .

Разряды чисел

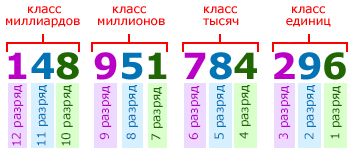
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.

Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:

Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:

• Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
• Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
• Сотни — единицами третьего разряда и пишутся на третьем месте справа.
• Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
• Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
• Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Пример. Запишите цифрами число, которое содержит:

1) 37 единиц второго класса и 565 единиц первого класса;

2) 450 единиц второго класса и 9 единиц первого класса;

3) 8 единиц второго класса и 50 единиц первого класса.

Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:

10 единиц	=	1 десяток;
10 десятков	=	1 сотня;
10 сотен	=	1 тысяча;
10 тысяч	=	1 десяток тысяч;
10 десятков тысяч	=	1 сотня тысяч;
10 сотен тысяч	=	1 тысяча тысяч (1 миллион);

Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.

Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.

Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде.

Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

24 527 — двадцать четыре тысячи пятьсот двадцать семь.

Источник

Разряды и классы чисел по математике — что это?

В начальных классах дети изучают «Разряды и классы чисел», однако эта тема вызывает много вопросов у родителей.

В этой статье Вы сможете «освежить» свои знания и объяснить ребенку эту тему.

Числа и цифры

ЧИСЛА — это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Для записи чисел используются специальные знаки — ЦИФРЫ.
Цифр десять: 1 2 3 4 5 6 7 8 9 0

Натуральные числа

НАТУРАЛЬНЫЕ ЧИСЛА — это числа, которые используются при счёте.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …,
1 — самое маленькое число, а самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль НЕ является натуральным числом.

Разряды и классы натуральных чисел

Для записи чисел используется ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. В десятичной системе счисления пользуются единицами, десятками единиц, десятками десятков — сотнями и т. д.
Каждая новая единица счёта больше предыдущей ровно в 10 раз:

Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).

Позиция (место) цифры в записи числа называется РАЗРЯДОМ. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.

Каждые три разряда натуральных чисел образуют КЛАСС.

Плакат «Сделай уроки сам!» 3-4 класс https://делайурокисам.рф

Основной вопрос, который родители часто задают: зачем ребенку эти знания? Ответ на этот вопрос очень простой — после изучения этого материала, дети переходят к таким темам как сложение и вычитание в столбик, где обязательно необходимо знать разряды числа, чтобы правильно вычислить примеры.

И если ребенок не освоит эту тему, тогда он не сможет правильно решать в столбик.

Складываем и вычитаем через разряды

Сложение столбиком

А) Складываем единицы: 4 + 3 = 7.
Записываем под единицами.
Б) Складываем десятки: 4 + 3 = 7.
Записываем под десятками.
В) Складываем сотни: 4 + 3 = 7.
Записываем под сотнями.
Ответ: 777

Вычитание столбиком

А) Вычитаем единицы: 9 – 3 = 6.
Записываем под единицами.
Б) Вычитаем десятки: 0 меньше,
чем 2, занимаем в сотнях (тысячах).

10 – 2 = 8. Записываем под десятками.
В) Вычитаем сотни: 9 – 4 = 5.
Записываем под сотнями.
Ответ: 586

Как приучить ребенка делать уроки самостоятельно?

Ваш ребенок до сих пор не может самостоятельно сесть и сделать уроки? Ждет от вас подсказок и указаний? Статья расскажет, как в короткие сроки изменить ситуацию и развить ответственное отношение к учебе. Читать далее

Как отучить ребёнка грызть ногти?

Эта статья расскажет о том, какие причины могут привести ребёнка к тому, что он грызёт ногти, в чём заключается вред и как отучить его от этой привычки. Читать далее

Подборка правил: деепричастие

Подборка правил: деепричастие. Читать далее

Почему ребенок не ценит вещи?

В статье рассказывается о том, как исправить проблему небрежного отношения к вещам у ребенка, подробно описаны рекомендации по поводу решения ситуации. Читать далее

Чем занять детей в дороге?

В статье рассказывается о том, чем можно занять ребенка в дороге. Читать далее

Источник