Что значит касательная параллельна прямой

Узнать ещё

Знание — сила. Познавательная информация

Касательная параллельна прямой

Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.

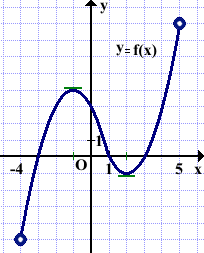
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.

Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.

На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.

Теперь рассмотрим аналогичное задание, в котором дан график производной функции.

2)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.

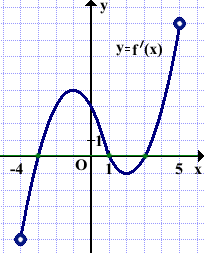
Угловой коэффициент касательной равен значению производной в точке касания: k₂=f'(x_o).

Значит, ищем точки, в которых значение производной равно нулю.

Таких точек три (с абсциссами x=-3, x=1 и x=3).

3)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=3x-11 или совпадает с ней.

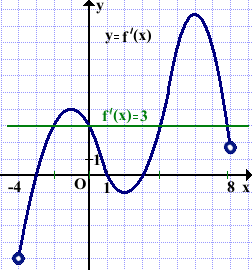
Поэтому ищем точки, в которых значение производной равно 3.

Таких точек в данном примере четыре.

4)На рисунке изображён график производной функции f(x). Найти абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=4-x или совпадает с ней.

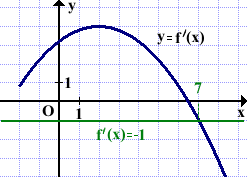
Ищем точку, в которой значение производной равно -1. Абсцисса этой точки x_o=7.

Источник

Уравнение касательной к графику функции

п.1. Уравнение касательной

Рассмотрим кривую \(y=f(x)\).
Выберем на ней точку A с координатами \((x_0,y_0)\), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке \(x_0\): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: \((y_B-y_A)=k(x_B-x_A)\).
Для \(A(x_0,y_0),\ B(x,y)\) получаем: \begin (y-y_0)=k(x-x_0)\\ y=k(x-x_0)+y_0\\ y=f'(x_0)(x-x_0)+f(x_0) \end

Чтобы записать уравнение касательной с угловым коэффициентом в виде \(y=kx+b\), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=\underbrace_<=k>x+\underbrace_ <=b>$$

п.2. Алгоритм построения касательной

На входе: уравнение кривой \(y=f(x)\), абсцисса точки касания \(x_0\).
Шаг 1. Найти значение функции в точке касания \(f(x_0)\)
Шаг 2. Найти общее уравнение производной \(f’ (x)\)
Шаг 3. Найти значение производной в точке касания \(f'(x_0 )\)
Шаг 4. Записать уравнение касательной \(y=f’ (x_0)(x-x_0)+f(x_0)\), привести его к виду \(y=kx+b\)
На выходе: уравнение касательной в виде \(y=kx+b\)

Пусть \(f(x)=x^2+3\). Найдем касательную к этой параболе в точке \(x_0=1\).

\(f(x_0)=1^2+3=4 \)
\(f'(x)=2x \)
\(f'(x_0)=2\cdot 1=2\)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: \(y=2x+2\)

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода \(x_0\notin D\), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку \(x_0\in D\), входящую в область определения. График функции и касательная имеют одну общую точку \((x_0,y_0)\).

Вертикальные касательные характерны для радикалов вида \(y=\sqrt[n]\).

Пусть \(f(x)=\sqrt[5]+1\). Найдем касательную к этой кривой в точке \(x_0=1\).

\(f(x_0)=\sqrt[5]<1-1>+1=1\)
\(f'(x)=\frac15(x-1)^<\frac15-1>+0=\frac15(x-1)^<-\frac45>=\frac<1><5(x-1)^<\frac45>> \)
\(f'(x_0)=\frac<1><5(1-1)^<\frac45>>=\frac10=+\infty\)
В точке \(x_0\) проходит вертикальная касательная.
Её уравнение: \(x=1\)
Ответ: \(y=2x+2\)

п.4. Примеры

Пример 1. Для функции \(f(x)=2x^2+4x\)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0\Rightarrow 2x(x+2)=0\Rightarrow \left[ \begin x=0\\ x=-2 \end \right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке \(x_0=0\): \begin f(x_0)=0,\ \ f'(x)=4x+4\\ f'(x_0)=4\cdot 0+4=4\\ y=4(x-0)+0=4x \end Касательная в точке \(x_0=-2\): \begin f(x_0)=0,\ \ f'(x)=4x+4\\ f'(x_0)=4\cdot (-2)+4=-4\\ y=-4(x+2)+0=-4x-8 \end

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: \(f'(x)=4x+4\) По условию \(f'(x_0)=tg\alpha=tg45^\circ=1\) Решаем уравнение: $$ 4x_0+4=1\Rightarrow 4x_0=-3\Rightarrow x_0=-\frac34 $$ Точка касания \(x_0=-\frac34\) \begin f(x_0)=2\cdot\left(-\frac34\right)^2+4\cdot\left(-\frac34\right)=\frac98-3=-\frac<15> <8>\end Уравнение касательной: \begin y=1\cdot\left(x+\frac34\right)-\frac<15><8>=x-\frac98 \end

в) найдите, в какой точке касательная будет параллельна прямой \(2x+y-6=0\). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: \(y=-2x+6\Rightarrow k=-2\). Касательная должна быть параллельной, значит, её угловой коэффициент тоже \(k=-2\). Получаем уравнение: \begin f'(x_0)=-2\\ 4x_0+4=-2\Rightarrow 4x_0=-6\Rightarrow x_0=-\frac32 \end Точка касания \(x_0=-\frac32\) \begin f(x_0)=2\cdot\left(-\frac32\right)^2+4\cdot\left(-\frac32\right)=\\ =\frac92-6=-\frac32 \end Уравнение касательной: \begin y=-2\cdot\left(x+\frac32\right)-\frac32=-2x-\frac92 \end Или, в каноническом виде: \begin 2x+y+\frac92=0 \end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой \(k=0\). Получаем уравнение: \(f'(x_0)=0\). \begin 4x_0+4=0\Rightarrow 4x_0=-4\Rightarrow x_0=-1 \end Точка касания \(x_0=-1\) \begin f(x_0)=2\cdot(-1)^2+4\cdot(-1)=-2 \end Уравнение касательной: \begin y=0\cdot(x+1)-2=-2 \end

Ответ: а) \(y=4x\) и \(y=-4x-8\); б) \(y=x-\frac98\); в) \(2x+y+\frac92=0\); г) \(y=-2\)

Пример 3*. Найдите точку, в которой касательная к графику функции \(f(x)=\frac-x\) перпендикулярна прямой \(y=11x+3\). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой \(k_1=11\).
Угловой коэффициент перпендикулярной прямой \(k_2=-\frac<1>=-\frac<1><11>\) \begin f'(x)=\left(\frac\right)’-x’=\frac<2x(x+3)-(x^2+2)\cdot 1><(x+3)^2>-1=\frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\\ =\frac<(x+3)^2>=- \frac<11> <(x+3)^2>\end В точке касания: \begin f'(x_0)=k_2\Rightarrow=-\frac<11><(x+3)^2>=-\frac<1><11>\Rightarrow (x+3)^2=121\Rightarrow (x+3)^2-11^2=0\Rightarrow\\ \Rightarrow (x+14)(x+8)=0\Rightarrow \left[ \begin x=-14\\ x=8 \end \right. \end
Уравнение касательной при \(x_0=-14\) \begin f(x_0)=\frac<(-14)^2+2><-14+3>+14=\frac<198><-11>+14=-18+14=-4\\ y=-\frac<1><11>(x+14)-4=-\frac <11>\end Уравнение касательной при \(x_0=8\) \begin f(x_0)=\frac<8^2+2><8+3>-8=\frac<66><11>-8=-2\\ y=-\frac<1><11>(x-8)-2=-\frac <11>\end
Ответ: точка касания (-14;-4), уравнение \(y=-\frac<11>\)
и точка касания (8;-2), уравнение \(-\frac<11>\)

Пример 4*. Найдите уравнения общих касательных к параболам \(y=x^2-5x+6\) и \(y=x^2+x+1\). Укажите точки касания.

Найдем производные функций: \begin f_1′(x)=2x-5,\ \ f_2′(x)=2x+1 \end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных \(g_1(x)\) и \(g_2(x)\) через эти переменные. \begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\\ \\ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) \end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: \begin \begin 2a-5=2b+1\\ 6-a^2=1-b^2 \end \Rightarrow \begin 2(a-b)=6\\ a^2-b^2=5 \end \Rightarrow \begin a-b=3\\ (a-b)(a+b)=5 \end \Rightarrow \begin a-b=3\\ a+b=\frac53 \end \Rightarrow \\ \Rightarrow \begin 2a=3+\frac53\\ 2b=\frac53-3 \end \Rightarrow \begin a=\frac73\\ b=-\frac23 \end \end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2\cdot\frac73-5=-\frac13,\ \ b=6-a^2=6-\frac<49><9>=\frac59 $$ Уравнение общей касательной: $$ y=-\frac x3+\frac59 $$
Точки касания: \begin a=\frac73,\ \ f_1(a)=\left(\frac73\right)^2-5\cdot\frac73+6=\frac<49><9>-\frac<35><3>+6=\frac<49-105+54><9>=-\frac29\\ b=-\frac23,\ \ f_2(b)=\left(-\frac23\right)^2-\frac23+1=\frac49-\frac23+1\frac<4-6+9><9>=\frac79 \end
Ответ: касательная \(y=-\frac x3+\frac59\); точки касания \(\left(\frac73;-\frac29\right)\) и \(\left(-\frac23;\frac79\right)\)

Пример 5*. Докажите, что кривая \(y=x^4+3x^2+2x\) не пересекается с прямой \(y=2x-1\), и найдите расстояние между их ближайшими точками.

Решим уравнение: \(x^4+3x^2+2x=2x-1\) \begin x^4+3x^2+1=0\Rightarrow D=3^2-4=5\Rightarrow x^2=\frac<-3\pm\sqrt<5>> <2>\end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, \(x\in\varnothing\) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом \(k=2\), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой \(y=2x-1\).
Строим уравнение касательной. По условию: \(f'(x)=4x^3+6x+2=2\) \begin 4x^3+6x=0\Rightarrow 2x(2x^2+3)=0\Rightarrow \left[ \begin x=0\\ 2x^2+3=0 \end \right. \Rightarrow \left[ \begin x=0\\ x^2=-\frac32 \end \right. \Rightarrow \left[ \begin x=0\\ x\in\varnothing \end \right. \Rightarrow x=0 \end Точка касания \(x_0=0,\ y_0=0^4+3\cdot 0^2+2\cdot 0=0\).
Уравнение касательной: \(y=2(x-0)+0=2x\)

Ищем расстояние между двумя параллельными прямыми: \(y=2x\) и \(y=2x-1\). Перпендикуляр из точки (0;0) на прямую \(y=2x-1\) имеет угловой коэффициент \(k=-\frac12\), его уравнение: \(y=-\frac12 x+b\). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и \(b=0\).

Уравнение перпендикуляра: \(y=-\frac x2\).
Находим точку пересечения прямой \(y=2x-1\) и перпендикуляра \(y=-\frac x2\): \begin 2x-1=-\frac x2\Rightarrow 2,5x=1\Rightarrow x=0,4;\ y=-\frac<0,4><2>=-0,2 \end Точка пересечения A(0,4;-0,2).
Находим расстояние \(OA=\sqrt<0,4^2+(-0,2)^2>=0,2\sqrt<2^2+1^2>=\frac<\sqrt<5>><5>\)
Ответ: \(\frac<\sqrt<5>><5>\)

Источник

Касательная к окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку ∠АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, ⌒АВ = 62°.

Если провести две касательных к окружности из одной точки, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично должны быть равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

sin BDA = AB : AD = 4,5 : 9 = 0,5

Мы знаем, что прямая, проложенная из точки до центра окружности, делит угол между касательными, проложенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN между ними равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности опускаются две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R) и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ ⌒АВ.

⌒АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

⌒КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Источник