Что значит измерить объем тела

Объем тела, его измерение.

Объем– это положительная скалярная величина, характеризующая размер геометрического тела.

Объемом тела называется положительная скалярная величина, определенная для каждого геометрического тела так, что:

1. равные тела имеют равные объемы;2. если тело составлено из нескольких тел, то его объем равен сумме их объемов.

Будем объем тела Q обозначать V(Q).Чтобы измерить объем тела, нужно выбрать единицу объема. Таковой является куб со стороной, равной единице длины, его объем равен е3. Измерение объема состоит в сравнении объема данного тела с объемом единичного куба. Результатом этого сравнения является такое число х такое, что V(Q) = х ∙ е3, которое называют численным значением объема при данной единице объема.Свойства численных значений объема1. Если тела равны, то равны и численные значения их объемов:

Q1 = Q2 V(Q1) = V(Q2). 2. Если тело Q состоит из тел Q1, Q2,…, Qn, то численное значение объема тела равно сумме численных значений объемов этих тел. 3. При замене единицы измерения объема численное значение объема увеличивается (уменьшается) во столько раз, во сколько раз уменьшается (увеличивается) единица объема. Выразим, например, 9 дм3 в кубических сантиметрах. Известно, что 1 дм3 = 1000 см3, и, следовательно, 9 дм3 = 9 ∙ 1 дм3 = 9 ∙ (1000 см3) = (9 ∙ 1000) ∙ см3 = = 9000 см3.

Для измерения объемов площадей используют стандартные единицы площади: м3, дм3, см3, мм3. Основная единица измерения объема – кубический метр. Соотношения между единицами объема: 10-9 км3 = 1м3 = 103дм3 = 106 см3 = 109 мм3. В начальной школе рассматривается объем прямоугольного параллелепипеда. Рассмотрим случай, когда длина, ширина и высота выражены натуральными числами. Если стороны основания равны а и b, то на это основание можно уложить а ∙ b единичных кубиков. Так как в высоту укладывается с таких слоев, то объем параллелепипеда вычисляется по формуле V = а ∙ b∙ с. Таким образом объем прямоугольного параллелепипеда равен произведению трех его измерений. В начальной школе изучается также такая величина, как емкость. Она рассматривается как объем сыпучих и жидких тел. Единица измерения емкости – литр. 1 л = 1 дм3. Измерить объемы тел более трудно, чем площадь фигур. Приведем несколько способов измерения объемов. 1. Правило Архимеда. Объем воды, вытесненной телом при погружении, равен объему этого тела. 2. Косвенный способ измерения объема. · Посредством измерения длин сторон и других отрезков и нахождения площади с помощью формул. · Нахождение объем через массу и плотность тела. 3. Метод дополнения (разбиения).

4. Объем (емкость) сосудов – с помощью наполнения.

Масса, ее измерения.

Определение. Массой тела называется положительная ве­личина, определенная для каждой фигуры так, что: 1) масса одинакова у тел, уравновешивающих друг друга на весах; 2) масса складывается, когда тела соединяются вместе: масса нескольких тел, взятых вместе, равна сумме их масс. Измерение массы производится с помощью весов. Выбираем тело е, масса которого принимается за единицу. Предполагается, что можно взять и доли этой массы. Например, если за единицу массы взят килограмм, то в процессе измерения можно использовать и такую его долю, как грамм: 1 г = 1/1000 кг. На одну чашку весов кладут тело, массу которого измеряют, а на другую – тела, выбранные в качестве единицы массы, т.е. гири. Этих гирь должно быть столько, чтобы они уравновесили первую чашку весов. В результате взвешивания получается численное значение массы данного тела при выбранной единице массы. Это значение приближенное. Например, если масса тела равна 5 кг 350 г, то число 5350 следует рассматривать как приближенное значение массы данного тела (при единице массы – грамм). Для численных значение массы справедливы все утверждения, сформулированные для длины, т.е. сравнение масс, действия над ними сводятся к сравнению и действиям над числовыми значениями масс (при одной и той же единице массы). Основная единица массы – килограмм. Из этой основной единицы образуются другие единицы массы: грамм, тонна и др.

Источник

Измерение объемов тела

Если вашей целью является снижение веса или наращение мышечной массы, измерьте свои параметры перед началом программы работы над собой. Многие привыкли отслеживать результаты с помощью весов. Но такой традиционный способ не является точным индикатором общего прогресса. Измерение объемов частей тела поможет вести более наглядный учет результатов.

Заведите специальный журнал и записывайте туда наблюдения за изменениями. Это не только придаст дополнительную мотивацию, но и поможет повторно отслеживать результаты своих действий, если вы решите взять паузу и отойти от тренировок на какое-то время. Ведение журнала не займет у вас много времени, а польза от него будет неоценимой.

Когда энтузиазм от первых тренировок начнет пропадать – загляните в журнал. То, чего вы уже добились, не даст вам отступить от цели на пути к стройному телу.

Теперь внимание! Подробно рассказываем, как точно измерить ваше тело с головы до пят.

Рассмотрим тело по зонам:

Шея. Многие люди начинают визуально худеть «сверху вниз». У них в первую очередь претерпевают изменения лицо и шея. Если вы относитесь к их числу, воспользуйтесь сантиметром, для измерения объема шеи. Измерьте область посредине шеи и запишите результат.

Плечи. Тем, кто задался целью нарастить мышечную массу, необходимо следить за изменением параметров плеч. Встаньте прямо и попросите кого-нибудь измерить сантиметром обхват ваших плеч.

Грудь. Эта часть тела правильно измеряется следующим образом: оберните сантиметр вокруг себя на уровне сосков. Зафиксируйте данные.

Бицепс. При измерении этой области учитывайте 2 параметра. Сначала измерьте мышцы в расслабленном, а затем в напряженном состоянии.

Талия. Для того, чтобы получить точные данные, оберните сантиметр вокруг талии на уровне пупка.

Бедра. Самая правильная область для измерения объема бедер – самая широкая их часть. Ориентиром послужат тазовые кости.

Область от бедер до колен. Чтобы правильно измерить эту область, отыщите середину между бедром и коленом. Измеряйте эту часть вашего тела в расслабленном состоянии, не напрягая мышц ног.

Икры ног. Изменение этих частей тела ничтожно мало даже при интенсивных физических нагрузках. И, тем не менее, не поленитесь. Выберите самую широкую часть икры, измерьте и запишите результат в журнал.

Советуем измерять параметры тела после пробуждения. Утром наш организм еще не отягощен пищей, которую он получит в течение дня. Таим образом, вы не рискуете приписать в журнал пару лишних сантиметров, например, в обхвате талии.

Повторяйте «замеры» своего тела через каждые 10-12 недель. Именно за такой временной период организм успевает перестроиться под новый режим тренировок, и можно говорить о каких-либо визуальных изменениях.

Эксперты рекомендуют. В зависимости от телосложения меняется и план работы над мышцами. Так эктоморфу логичнее начать с прокачки плеч. Эндоморфу же необходимо уменьшить объем талии.

Не расстраивайтесь, если первое время результаты будут незначительными. Даже это – большая победа над собой. Радуйтесь самым маленьким изменениям в своих параметрах, хвалите себя за достижения и двигайтесь дальше.

Автор статьи: Саманта Клейтон. Призер Олимпийских игр, фитнес-эксперт, директор по вопросам фитнес обучения Herbalife.

Если вы хотите связаться с Индивидуальным консультантом, который поможет вам сформировать программу тренировок, перейдите по ссылке :

Источник

Объемы геометрических тел

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

• V сохраняется при движениях.
• V удовлетворяет принципу Кавальери.
• Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
• Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

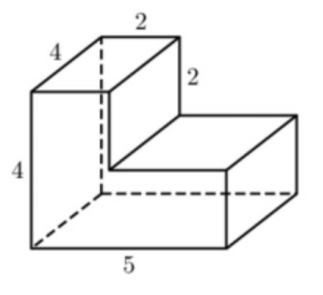
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

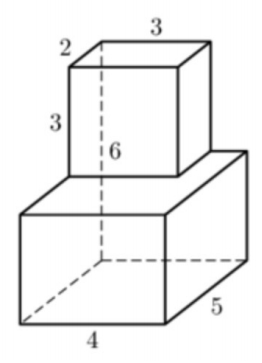
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Разберем, как можно вычислять объемы изучаемых в школе фигур.

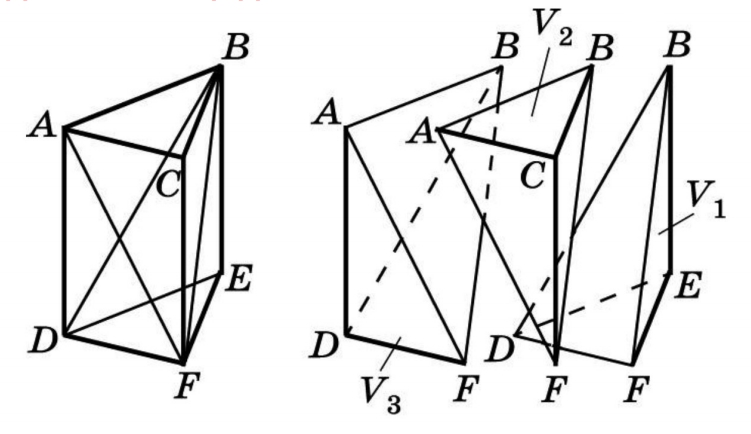
Объем призмы

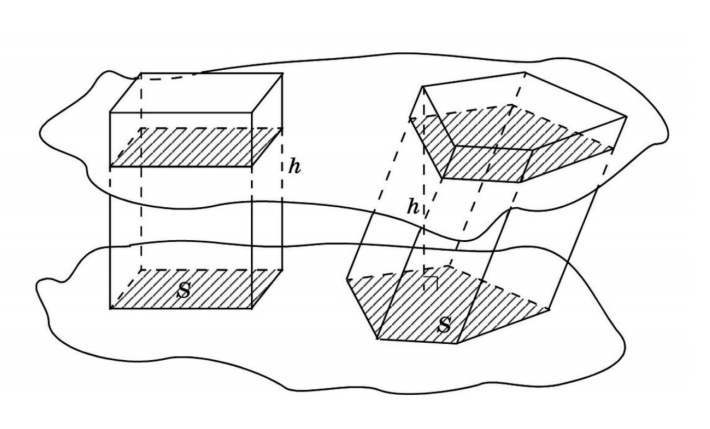
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

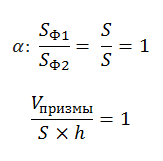
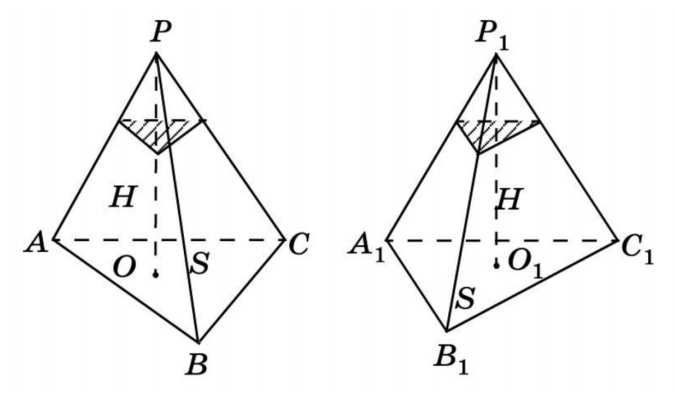
Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

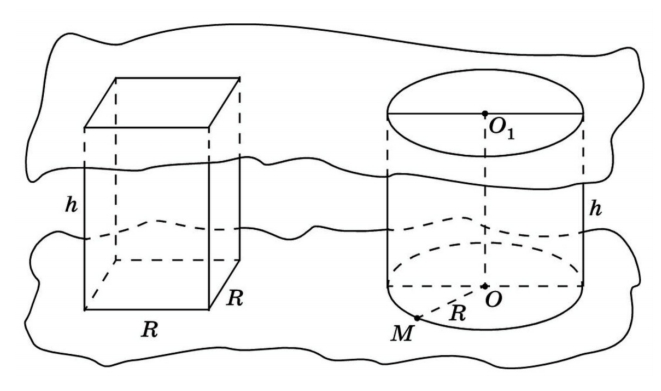
Объем цилиндра

Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

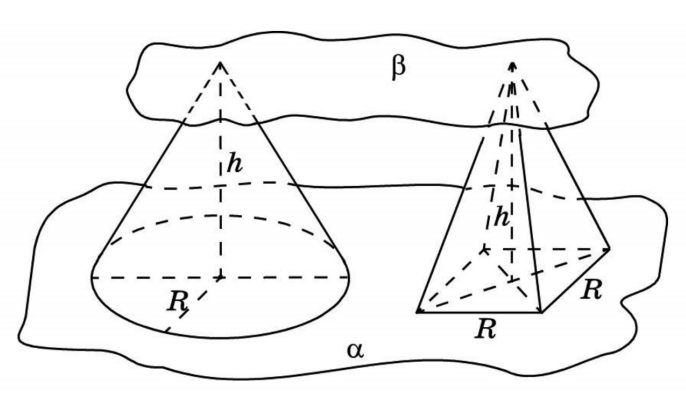
Объем конуса

Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте «Математические этюды» , где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR 2 . Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x 2 . Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R 2 — x 2 ).

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

Источник