искомое
Русско-английский словарь математических терминов. — Американское математическое общество . Э.Д. Лоувотер . 1990 .
Смотреть что такое «искомое» в других словарях:
Искомое — ср. 1. То, что следует найти, отыскать. 2. То, что найдено. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
искомое — ого; ср. Матем. Величина, которую следует определить, установить … Энциклопедический словарь
Искомое — компонент интеллектуальной задачи, составляющий цель действия … Современный образовательный процесс: основные понятия и термины
искомое — ого; ср.; матем. Величина, которую следует определить, установить … Словарь многих выражений
искомое выражение — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN desired expression … Справочник технического переводчика
искомое значение — заданная величина ожидаемое значение требуемое значение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы заданная величинаожидаемое… … Справочник технического переводчика
ИСКОМЫЙ — ИСКОМЫЙ, искомая, искомое (книжн.). 1. Подлежащий определению посредством вычислений (мат.). Искомый коэфициент. Искомая величина. Искомое выражение. 2. в знач. сущ. искомое, искомого, ср. Величина, которую следует определить посредством… … Толковый словарь Ушакова
Линейный поиск — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Линейный, последовательный поиск алгоритм нахождения заданного значения произвольной функции на некотором отрезке. Данный алгоритм являе … Википедия
Сахар свекловичный и тростниковый* — I. Химия. II. Техническое производство. III. Статистика. IV. Акциз на сахар. V. Сахарная нормировка. VI Сахар в международной торговле. I. С. (хим. С 12 Н 22 О 11). Нахождение и добывание свекловичного и тростникового С. см. ниже. С.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сахар свекловичный и тростниковый — I I. Химия. II. Техническое производство. III. Статистика. IV. Акциз на сахар. V. Сахарная нормировка. VI Сахар в международной торговле. I. С. (хим. С12Н22О11). Нахождение и добывание свекловичного и тростникового С. см. ниже. С. кристаллизуется … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
дальномер — прибор для определения расстояний до наблюдаемых объектов без непосредственных измерений на местности, в пространстве. По принципу действия дальномеры подразделяются на две основные группы: первую составляют оптические дальномеры; во вторую… … Энциклопедия техники
Источник
ВОЗ оценила скорость распространения омикрон-штамма
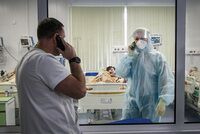
Фото: Denis Balibouse / Reuters
Эксперты Всемирной организации здравоохранения (ВОЗ) оценили скорость распространения нового штамма коронавируса омикрон. По последним данным, есть значительные подтверждения того, что омикрон распространяется гораздо быстрее других видов инфекции. Об этом сообщил гендиректор ВОЗ Тедрос Аданом Гебрейесус, передает РИА Новости.
Теперь у нас есть убедительные доказательства того, что омикрон распространяется значительно быстрее штамма дельта
Гебрейесус также подтвердил, что вирус опасен в том числе и для привитых и переболевших коронавирусной инфекцией.
Омикрон-штамм
Представитель Всемирной организации здравоохранения по борьбе с COVID-19 Дэвид Набарро отметил, что омикрон распространяется чрезвычайно быстро По данным ВОЗ, число новых случаев удваивается каждые два-три дня.
Это значит, что ситуация будет в восемь раз серьезнее через неделю и в 40 раз серьезнее через две недели
При этом основные симптомы омикрон-штамма коронавируса принципиально не отличаются от предыдущих штаммов. По словам представителя ВОЗ в России Мелиты Вуйнович, в список наиболее распространенных проявлений заболевания вошли головная боль, температура и поражение легких, бывают и осложнения, которые ВОЗ отмечала во всех штаммах до сих пор.
Таким образом, понять, кто заболел омикроном, а кто — дельтой, клинически сейчас уже практически невозможно, подчеркнула эксперт.
Вуйнович также предположила, что омикрон-штамм коронавируса может стать «живой вакциной» от COVID-19 и позволит победить пандемию. Она отметила, что такой итог возможен, но подчеркнула, что на сегодняшний день говорить об этом рано, поскольку пациентов с омикроном недостаточно. «Надо подождать не менее недели-полутора, чтобы мы могли точно сказать», — пояснила Вуйнович.
Прогноз на ближайший год
По прогнозам ВОЗ, пандемия коронавируса может завершиться уже в следующем году. Однако, подчеркнул Гебрейесус в ходе брифинга, положить конец COVID-19 удастся, только остановив распространение вируса.
Если мы хотим, чтобы пандемия закончилась в следующем году, мы должны покончить с неравенством и вакцинировать 70 процентов населения каждой страны к середине следующего года
Приблизительно такие же временные рамки ставят и врачи московской городской клинической больницы №52. По их предположениям, пандемия коронавируса может продлиться еще полгода или год.
В свою очередь, директор Европейского регионального бюро Всемирной организации здравоохранения (ВОЗ) Ханс Клюге выразил надежду, что рано или поздно произойдет эволюция от пандемии коронавируса до эндемии, как это произошло с гриппом: тогда COVID-19 перейдет в разряд сезонных респираторных вирусов, от которых людям необходимо делать прививку раз в год.
Ситуация в России
Представитель ВОЗ в России Мелита Вуйнович отметила, что в России видны признаки выхода на плато по COVID-19 и изменение эпидемической ситуации. При этом она обратила внимание, что, несмотря на выход на плато, уровень заболеваемости в стране очень высокий, «близкий к 30 тысячам случаев в день». «Видны хорошие знаки, но не надо абсолютно успокаиваться», — призвала Вуйнович.
Источник
Скорость, Вектор скорости и траектория, Сложение скоростей
Скорость
Средняя скорость частицы характеризует быстроту ее движения за конечный промежуток времени. Неограниченно уменьшая этот промежуток, мы придем к физической величине, характеризующей быстроту движения в данный момент времени. Такая величина называется мгновенной скоростью или просто скоростью:
обозначает математическую операцию перехода к пределу. Под этим символом записывается условие, при котором выполняется данный предельный переход; в рассматриваемом случае это стремление к нулю промежутка времени. При вычислении скорости по этому правилу мы убедимся, что уменьшение промежутка времени приводит к тому, что на некотором этапе получаемые очередные значения средней скорости будут все меньше и меньше отличаться друг от друга. Поэтому на практике при нахождении скорости можно остановиться на конечном значении, достаточно малом для получения требуемой точности значения скорости.
Вектор скорости и траектория.
Рассматриваемый предельный переход имеет ясный геометрический смысл. Поскольку вектор перемещения направлен по хорде, соединяющей две точки траектории, то при сближении этих точек, происходящем при, он принимает положение, соответствующее касательной к траектории в данной точке. Это значит, что вектор скорости направлен по касательной к траектории. Так будет в любой точке траектории (рис. 14). При прямолинейной траектории движения вектор скорости направлен вдоль этой прямой.
Скорость прохождения пути.
Аналогичным переходом определяется мгновенная скорость прохождения пути:
Для плавной кривой, каковой является траектория любого непрерывного механического движения, длина дуги тем меньше отличается от длины стягивающей ее хорды, чем короче эта дуга. В пределе эти длины совпадают. Поэтому при можно считать, что . Это означает, что скорость прохождения пути равна модулю мгновенной скорости . Движение, при котором модуль скорости остается неизменным, называется равномерным. В случае прямолинейной траектории при равномерном движении вектор скорости постоянен, а в случае криволинейной траектории изменяется только его направление.
Сложение скоростей.
Если тело одновременно участвует в нескольких движениях, то его скорость равна векторной сумме скоростей каждого из этих движений. Это непосредственно следует из правила сложения перемещений: так как , то после деления на получаем
Иногда бывает удобно представить некоторое сложное движение как суперпозицию, т. е. наложение двух простых движений. В этом случае равенство (3) можно трактовать как правило разложения вектора скорости на составляющие.
По этой ссылке вы найдёте полный курс лекций по математике:
Задачи.
1.
Переправа через реку. Скорость течения в реке с параллельными берегами всюду одинакова и равна. Ширина реки (рис. 15). Катер может плыть со скоростью относительно воды. На какое расстояние s снесет катер вниз по течению реки, если при переправе нос катера направить строго поперек берегов?
Катер участвует одновременно в двух движениях: со скоростью , направленной поперек течения, и вместе с водой со скоростью которая направлена параллельно берегу. В соответствии с правилом сложения скоростей полная скорость катера относительно берегов равна векторной сумме (рис. 16). Очевидно, что движение катера происходит по прямой, направленной вдоль вектора. Искомое расстояние s, на которое снесет катер при переправе, можно найти из подобия треугольника, образованному векторами скоростей:
Эту задачу легко решить и не прибегая к сложению векторов скоростей.
Очевидно, что расстояние s равно произведению скорости течения на время в течение которого катер пересекает реку. Это время можно найти, разделив ширину реки на скорость движения катера поперек реки. Таким образом, находим Рис. 16. Сложение скоростей при переправе через .В этой простой задаче второй способ решения предпочтительнее, так как он проще. Однако уже при небольшом усложнении условия задачи становятся отчетливо видны преимущества первого способа, основанного на сложении векторов скоростей.
2. Переправа поперек реки. Предположим, что теперь нам нужно переправиться на катере через ту же реку точно поперек, т. е. попасть в точку В, лежащую напротив начальной точки А (рис. 17). Как нужно направить нос катера при переправе? Сколько времени займет такая переправа?Решение. В рассматриваемом случае полная скорость v катера относительно берегов, равная векторной сумме скоростей должна быть направлена поперек реки.
Из рис. 17 сразу видно, что вектор, вдоль которого и смотрит нос катера, должен отклоняться на некоторый угол а вверх по течению реки от направления . Синус этого угла равен отношению модулей скоростей течения и катера относительно воды. Переправа поперек реки без сноса возможна только в том случае, когда скорость катера относительно воды больше скорости течения. Это сразу видно либо из треугольника скоростей на рис. 17 (гипотенуза всегда больше катета), либо из формулы (синус угла а должен быть меньше единицы).Время переправы найдем, разделив ширину реки на полную скорость катера по теореме Пифагора.
Возможно вам будут полезны данные страницы:
3. Снос при быстром течении.
Предположим теперь, что скорость катера относительно воды меньше скорости течения: В таком случае переправа без сноса невозможна. Как следует направить нос катера при переправе, чтобы снос получился минимальным? На какое расстояние этом снесет катер? Решение. Полная скорость относительно берегов во всех рассматриваемых случаях дается формулой. Однако теперь нагляднее выполнить сложение векторов и по правилу треугольника (рис. 18) первым изображаем век гор для которого мы знаем модуль направление, а затем к его концу пристраиваем начало вектора известен только модуль, направление еще предстоит выбрать. Этот выбор нужно сделать так, вектор результирующей скорости как можно меньше отклонялся от направления поперек реки.
Рис. 19. Определение курса (направление вектора) переправы минимальным сносом 18. Сложение скоростей переправе Конец любом направлении должен лежать на окружности радиуса центр которой совпадает концом вектора. Эта окружность показана Так условию задачи то точка соответствующая началу лежит вне этой окружности.
| Из рисунка видно, что образует прямой |
наименьший угол тогда, когда он направлен касательной Следовательно, перпендикулярен вектору треугольник прямоугольный. Таким образом, направлять вверх течению под углом линии Синус этого угла дастся выражением Траектория направлена вдоль вектора, т.е. она перпендикулярна направлению, в котором смотрит катера. Это значит, своей траектории катер движется боком. другом берегу реки причалит точке, до найти из подобия треугольников. Модуль находится теореме Пифагора. результате получаем
4. Лодка тросе. Лодку подтягивают за привязанный носу трос, наматывая равномерно вращающийся барабан Барабан установлен высоком берегу. какой скоростью лодка тот момент, трос горизонтом? Трос выбирается барабаном скоростью.
Решение.
Точка троса, где он привязан к лодке, движется с той же скоростью, что и лодка. Эта скорость v направлена горизонтально. Чтобы связать ее со скоростью выбирания троса, нужно сообразить, что движение троса сводится к повороту вокруг точки В, где он касается барабана, и скольжению вдоль собственного направления, т. е. прямой . Поэтому естественно разложить скорость точки на две составляющие , направленные вдоль и поперек троса (рис. 21). Скорость , направленная поперек, связана с поворотом троса. Модуль скорости направленной вдоль троса, — это и есть данное в условии задачи значение скорости.
По мере приближения лодки к берегу угол а становится больше. Это значит, что cos а убывает и искомая скорость возрастает. Задача для самостоятельного решения Человек находится в поле на расстоянии от прямолинейного участка шоссе. Слева от себя он замечает движущийся по шоссе автомобиль. В каком направлении следует бежать к шоссе, чтобы выбежать на дорогу впереди автомобиля и как можно дальше от него? Скорость автомобиля и, скорость человека.
• Объясните, почему вектор скорости всегда направлен по касательной к траектории.
• В некоторых случаях траектория движения частицы может иметь изломы. Приведите примеры таких движений. Что можно сказать о направлении скорости в точках, где траектория имеет излом?
• В случае непрерывного механического движения вектор скорости не испытывает скачков ни по модулю, ни по направлению. Появление скачков скорости всегда связано с некоторой идеализацией реального процесса. Какие идеализации присутствовали в приведенных вами примерах траекторий с изломами?
• Найдите ошибку в приводимом ниже решении задачи 4. Разложим скорость , точки троса на вертикальную и горизонтальную составляющие (рис. 22). Горизонтальная составляющая это и есть искомая скорость лодки. Поэтому и (неверно!).
Скорость как производная.
Вернемся к выражению (1) для мгновенной скорости. При движении частицы ее радиус-вектор г изменяется, т. е. является некоторой функцией времени:. Перемещение Дг за промежуток времени At представляет собой разность радиусов-векторов в моменты времени. Поэтому формулу (1) можно переписать в виде В математике такую величину называют производной от функции по времени Для нее используют следующие обозначения. Последнее обозначение (точка над буквой) характерно именно для производной по времени. Отметим, что в данном случае производная представляет собой вектор, так как получается в результате дифференцирования векторной функции по скалярному аргументу. Для модуля мгновенной скорости в соответствии справедливо выражение в начале статьи.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник