Что значит интегрированная функция

Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций

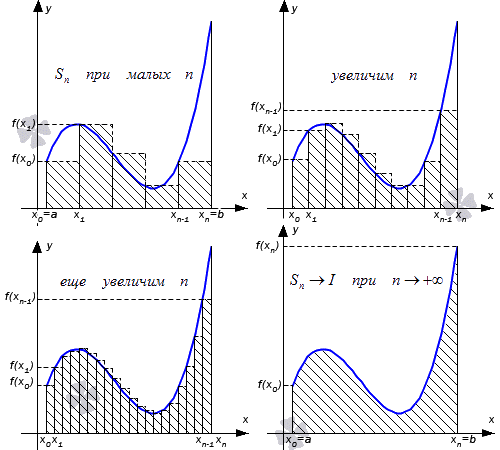
Определение интеграла было дано еще в школе при вычислении площади криволинейной трапеции. Была рассмотрена непрерывная неотрицательная функция y = f ( x ) на отрезке [ a ; b ] , тогда сам отрезок развивался на n равных частей точками a = x 0 x 1 x 2 . . . x n — 1 x n = b . Отсюда получали, что площадь криволинейной трапеции была представлена в виде площадей элементарных треугольников

S n = f ( x 0 ) · ( x 1 — x 0 ) + f ( x 1 ) · ( x 2 — x 1 ) + . . . + f ( x n — 1 ) · x n — x n — 1 = = f ( x 0 ) · b — a n + f ( x 1 ) · b — a n + . . . + f ( x n — 1 ) · b — a n = = b — a n · f ( x 0 ) + f ( x 1 ) + . . . + f ( x n — 1 )

Значение данного выражения стремилось к числу I при бесконечном увеличении количества точек разбиения отрезка [ a ; b ] .

После обобщения выражения и определения получили, что любая непрерывная функция y = f ( x ) с числом I имеет отрезок, который и получил название определенного интеграла.

Его геометрическое понятие было показано в школе в 11 классе. Рассмотрим рисунок, приведенный ниже. Имеем изображение определенного интеграла.

В данной статье будет показано определения определенного интеграла, которые были заданы Риманом и Дарбу, Ньютоном-Лейбницом. Подробно будет показано условие интегрируемости функции на заданном определенном отрезке с перечислением интегрируемых функций.

Определенный интеграл Римана

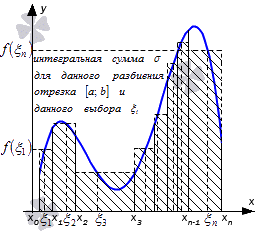
Рассмотрим функцию y = f ( x ), которая определяется на заданном отрезке [ a ; b ] . Необходимо разбить даны отрезок на n количество частей x i — 1 ; x i , i = 1 , 2 , . . . , n точками a = x 0 x 1 x 2 . . . x n — 1 x n = b . Примем обозначение λ = m a x i = 1 , 2 , . . . , n ( x i — x i — 1 ) , а сами точки x i , i = 1 , 2 , . . . , n — 1 необходимо выбрать таким образом, чтобы λ → 0 при n → + ∞ . В выбранном отрезке x i — 1 ; x i , i = 1 , 2 , . . . , n необходимо выбрать точку ζ i . При заданных условиях существует множество способов выбора точек x i , i = 1 , 2 , . . . , n — 1 и ζ i , i = 1 , 2 , . . . , n .

Интегральная сумма функции y = f ( x ) для разбиения отрезка [ a ; b ] с выбором точек ζ i , i = 1 , 2 , . . . , n является выражение вида:

σ = f ( ζ 1 ) · x 1 — x 0 + f ( ζ 2 ) · x 2 — x 1 + . . . + f ( ζ n ) · ( x n — x n — 1 ) = = ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 )

Рассмотрим рисунок, приведенный ниже.

Для того, чтобы разбить заданный отрезок [ a ; b ] и выбрать точки ζ i , i = 1 , 2 , . . . , n , получаем интегральную сумму. Иначе говоря, получаем множество интегральных сумм с различными вариациями выбора x i , i = 1 , 2 , . . . , n и ζ i , i = 1 , 2 , . . . , n .

Число I называют пределом интегральных сумм σ при λ → 0 , когда любое малое положительное эпсилон ε > 0 имеет место быть малым положительным, зависящим от эпсилон, причем δ ( ε ) > 0 , с λ δ , тогда при выборе точек ζ i , i = 1 , 2 , . . . , n неравенство σ — I ε считается справедливым.

Интегрируемой на отрезке [ a ; b ] функцией y = f ( x ) называют такую функцию, у которой имеется конечный предел ее интегральных сумм при λ → 0 . Данное значение предела называют определенным интегралом Римана.

За обозначение интеграла Римана принято брать выражение вида ∫ a b f ( x ) d x . Из определения получим, что определенный интеграл Римана записывается так: ∫ a b f ( x ) d x = lim λ → 0 σ .

Числа a и b называют нижним и верхним пределом интегрирования, а f ( x ) – подынтегральная функция, где x – переменная интегрирования.

Значение определенного интеграла Римана не зависит от переменной интегрирования , тогда получаем интеграл вида ∫ a b f ( x ) d x = ∫ a b f ( t ) d t = ∫ a b f ( u ) d u = ∫ a b f ( q ) d q .

Определенный интеграл Дарбу

Чтобы понять необходимо и достаточное условие существования определенного интеграла Дарбу, необходимо применить несколько определений.

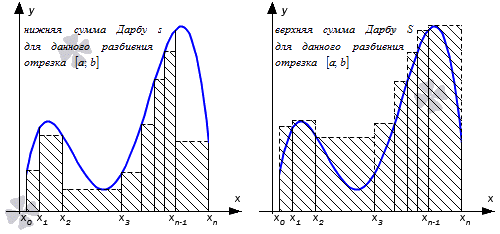
Возьмем на рассмотрение функцию y = f ( x ) , определенную на отрезке [ a ; b ] . Необходимо разбить заданный отрезок на n количество частей при помощи точек a = x 0 x 1 x 2 . . . x n — 1 x n b с условием λ → 0 при n → + ∞ . Тогда m i и M i являются нижней и верхней гранью множества значений заданной функции на i -ом отрезке i = 1 , 2 , . . . , n . Получаем, что для непрерывной и ограниченной функции m i = m i n x ∈ x i — 1 ; x i f ( x ) , M i = m a x x ∈ x i — 1 ; x i f ( x ) , i = 1 , 2 , . . . , n .

s = m 1 · ( x 1 — x 0 ) + m 2 · ( x 2 — x 1 ) + . . . + m n · ( x n — x n — 1 ) = = ∑ i = 1 n m i · ( x i — x i — 1 )

S = M 1 · ( x 1 — x 0 ) + M 2 · ( x 2 — x 1 ) + . . . + M n · ( x n — x n — 1 ) = = ∑ i = 1 n M i · ( x i — x i — 1 )

для разбиения отрезка [ a ; b ] называют нижней и верхней суммами Дарбу.

Рассмотрим рисунок, приведенный ниже.

Отсюда видно, для того, чтобы разбиение данного отрезка было фиксированным, необходимо использовать двойное неравенство s ≤ σ ≤ S , которое является справедливым. Иначе говоря, s и S считаются нижней и верхней гранями множества интегральных сумм.

Интегрируемость функции y = f ( x ) на отрезке [ a ; b ] должна иметь достаточное условие, которое дает предел разности верхней и нижней сумм Дарбу равным нулю при λ → 0 , тогда условие lim λ → 0 ( S — s ) = 0 выполняется. Это и есть необходимое и достаточное условие существования определенного интеграла Дарбу, который так и получил название определенный интеграл Дарбу. Его обозначение записывается в виде ∫ a b f ( x ) d x .

Определенный интеграл Ньютона-Лейбница

Рассмотрим подробно понятие определенного интеграла Ньютона-Лейбница.

Если функция вида y = f ( x ) имеет первообразную F ( x ) , определенную на отрезке [ a ; b ] , со значением первообразной в точке х = а равняется нулю, то есть F ( a ) = 0 . Определенный интеграл Ньютона-Лейбница — значение первообразной в точке интегрирования b , тогда получаем выражение вида ∫ a b f ( x ) d x = F ( b ) при F ( a ) = 0 .

Данное определение связано в формулой Ньютона-Лейбница ∫ a b f ( x ) d x = F ( b ) — F ( a ) . В ней F ( x ) является первообразной из множества, а определенный интеграл имеет первообразную, которая становится равной нулю при х = а .

Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций

Рассмотрим необходимое условие существования определенного интеграла функции на отрезке.

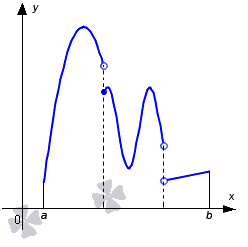
Когда функция вида y = f ( x ) интегрируема на отрезке [ a ; b ] , то имеется в виду, что она им ограничена. Условие считается необходимым, но не достаточным, так как функция ограничена отрезком, при этом она не всегда на нем интегрируема. Это условие применяют для проверки возможности интегрирования имеющейся функции на заданном отрезке. Иначе говоря, проверяется ее ограниченность.

Виды функций, для которых существует определенный интеграл:

• когда функция непрерывна на отрезке [ a ; b ] , значит интегрируема;
• когда функция ограничена на отрезке [ a ; b ] и непрерывна в точках, кроме конечного числа, тогда считается, что она интегрируема на отрезке [ a ; b ] .

Рассмотрим рисунок, приведенный ниже. На нем располагается пример интегрируемой функции.

Итоги

Задавание определенного интеграла Римана происходит через предел интегральных сумм, а интеграл Дарбу – предел разности верхних и нижних сумм Дарбу, в свою очередь интеграл Ньютона-Лейбница – при помощи значения первообразной.

Одновременное существование интеграла Римана и Ньютона-Лейбница, определенных на отрезке [ a ; b ] , возможно, при этом их значения будут равными. Для ограниченной функции существование определенного интеграла Дарбу и Римана невозможно.

Источник

Интегралы для чайников: как решать, правила вычисления, объяснение

• 4 июня 2021 г.
• 10 минут
• 845 341
• 26

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник