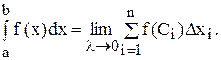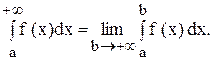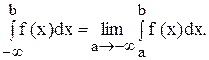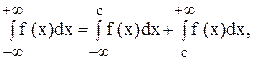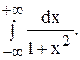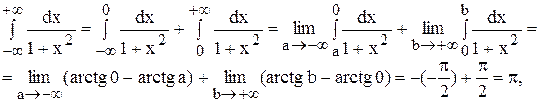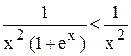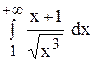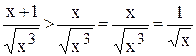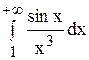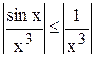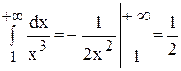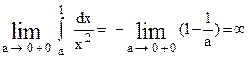Абсолютная и условная сходимость несобственных интегралов
Абсолютная и условная сходимость несобственных интегралов
- Абсолютная и условная фокусировка неправильных интегралов. Вводится понятие А Б О Л Ь т н о г и М СЛ о ВН о г сходимости-376CH. 9. Очистить Интеграл Римана НТИ Интеграл. Пусть f (x)интегрируемо для любого отрезка[a, L]*. * Тогда функция|f (x) l интегрируема для
любого отрезка[a, L]. **Это означает, что примитив G (x), который может быть определен как f (t) dt, удовлетворяет неравенству|F (x)|для всех x^a, где D — Парковка. О П Р Е Д Е Л Е Н и Е1. Неправильный Интеграл\f (x) dx обусловлен абсолютным t, но если J\f (x)\dx
сходится, то это X o d I и m s I. Но 4-х О П Р Е Д Е Л Е Н и Е2. Некорректный Людмила Фирмаль
Интеграл\f (x) d x n-а зывается у С Л О В Н О С Х О я щ и м ы я, если он сходится, а в -+“ Они > \f(x)\dx расходятся. А з а м е ч а н и Е. Если поставить утверждение 2g(X)=|f (X)|>m s, то можно увидеть, что абсолютная сходимость неправильного интеграла означает сходимость. Утверждения 2 и 3 могут только установить абсолютную
сходимость изученных некорректных интегралов. Приведем еще одно указание на сходимость неправильных интегралов первого рода, пригодных для установления этой интегральной и условной сходимости. U t V E R W d e n I E 4 (p R I z n A K D I R I x l e-A belya).. 1) непрерывная функция f(x) a L1 полупрямой A. получаем j f ( * ) g ( * ) dx=F(x) g (x)|J — [F(x)g'(x) dx. (9.1.7) В В зависимости от условий
- теоремы, F(x) ограничивается:\F (x)\+OO, g (x) s>0 и gy(x) 0, поэтому, если вы выберете B для этого e, вы можете гарантировать, что G(Ai) B. Таким образом, и из неравенства (9.1.8) он содержит большое in, неравенство I f f (x) g (x) dx / Людмила Фирмаль
Рассмотрим Интеграл Френеля J sinx2dx. Отчет Sin2x= — — — — cos2xh Интеграл I A в OCictCH2z V2x- DX конвергенция (в Один. для f (x)=cos2x, g (x)=l/(2xa), для 0
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
Несобственные интегралы
1. Несобственные интегралы с бесконечными пределами
Вспомним определение интеграла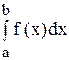 
как предела интегральных сумм: 
В определении предполагается, что интервал интегрирования конечен, а функция f (x) непрерывна в нем. Нарушение этих предположений приводит к несобственным интегралам.
Определение. Если интеграл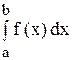 
стремится к конечному пределу при неограниченном возрастании “b”, то этот предел называют несобственным интегралом с бесконечной верхней границей от функции f (x) и обозначают символом 
В этом случае говорят, что несобственный интеграл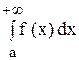 
существует или сходится.
Если указанный предел не существует или существует, но бесконечен, то говорят, что интеграл не существует или расходится.
Аналогично определяется несобственный интеграл с бесконечной нижней границей:
Несобственный интеграл с двумя бесконечными границами определяется формулой:
где с — любая фиксированная точка на оси Ох.
Итак, несобственные интегралы могут быть с бесконечно нижней границей, с бесконечно верхней границей, а также с двумя бесконечными границами.
Признаки сходимости. Абсолютная и условная сходимость
Интеграл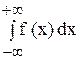 
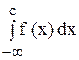
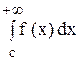
существует только тогда, когда существует каждый из интегралов: 
и 
.
Пример. Исследовать на сходимость интеграл 
Полагая с = 0, получим:
т.е. интеграл сходится.
Иногда нет необходимости вычислять несобственный интеграл, а достаточно лишь знать, сходится он или расходится, сравнив его с другим интегралом.
Теорема сравнения несобственных интегралов.
Пусть в интервале [a; +¥) функции f (x) и j (х) непрерывны и удовлетворяют неравенству 0 £ j (x) £ f (x). Тогда:
а) если интеграл 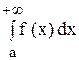сходится, то сходится 
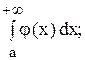
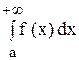
б) если интеграл расходится, то также расходится.
Пример.1. Исследовать, сходится ли интеграл:
Решение. Заметим, что при 1 £ x :
= 1
Следовательно, 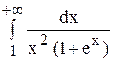сходится и его значение, меньше 1.
Пример. 2. Исследовать, сходится ли интеграл
Замечаем, что 
Но,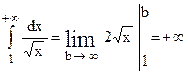 
.
Следовательно, расходится и данный интервал.
Теорема. Если интеграл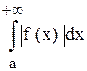 
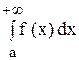
сходится, то сходится и интеграл .
В этом случае последний интеграл называется абсолютно сходящимся.
Если интеграл от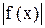 
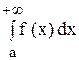
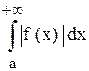
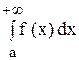
расходится, то об интеграле от f (x) на одном этом основании ещё ничего сказать нельзя: он может расходиться, а может и сходиться. В последнем случае (т.е. когда сходится, 
расходится говорят, что сходится условно (не абсолютно).
Пример. Исследовать сходимость интеграла
Здесь подынтегральная функция – знакопеременная.
Замечаем, что 
Но 
Следовательно, интеграл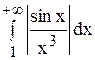 
сходится.
Отсюда следует, что сходится и данный интеграл.
Итак, для определения сходимости несобственного интеграла можно его сравнивать с другим интегралом, который заведомо сходится или расходится.
Несобственные интегралы от разрывных функций
Если на отрезке [a; b] функция f (x) имеет несколько (конечное число) точек разрыва первого рода, это “препятствие” легко устранить, разбив отрезок точками разрыва на несколько отрезков, вычислить определенные интегралы на каждом отдельном участке и результаты сложить.
Рассмотрим определенный интеграл от функции, неограниченной при приближении к одному из концов отрезка [a; b], например,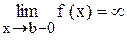 
.
(В таких случаях обычно говорят : ’’Функция имеет бесконечный разрыв на правом конце отрезка интегрирования’’.)
Ясно, что обычное определение интеграла здесь теряет свой смысл.
Определение. Несобственным интегралом от функции f(x), непрерывной при а £ х 
Значит на участке [0, 1)] интеграл также расходится.
Таким образом, данный интеграл расходится на всем отрезке [-1, 1]. Отметим, что если бы мы стали вычислять данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке x = 0, то получили бы неверный результат. Действительно,
, что невозможно.
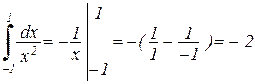
Итак, для исследования несобственного интеграла от разрывной функции, необходимо «разбить» его на несколько интегралов и исследовать их.
Источник
