Что значит группировки слагаемых

Группировка слагаемых и множителей, правило, примеры.

К суммам трех и большего количества слагаемых относится тождественное преобразование, имеющее название группировка слагаемых. Аналогичный вид преобразований существует и для произведений трех, четырех и т.д. множителей, называемый группировкой множителей. В этой статье мы разберем правила группировки слагаемых и множителей, и рассмотрим применение этих правил на примерах.

Навигация по странице.

Группировка слагаемых, примеры

В числовых и буквенных выражениях, содержащих суммы трех и большего количества слагаемых, можно выполнять группировку слагаемых. Что же понимают под этим термином?

Под группировкой слагаемых подразумевается совместное рассмотрение нескольких слагаемых в сумме. Иными словами, группировка слагаемых – это объединение слагаемых в группу.

Существует правило группировки слагаемых: сначала в исходной сумме выполняется перестановка слагаемых так, чтобы группируемые слагаемые оказались рядом, после чего они заключаются в скобки.

Прежде чем перейти к рассмотрению примеров, поясним, на чем основано приведенное правило группировки слагаемых. Оно базируется на переместительном и сочетательном свойстве сложения.

Переходим к примерам. Рассмотрим сумму трех слагаемых вида 1+2+3 . Пусть мы хотим выполнить группировку первого и второго слагаемых. В этом случае нам не нужно выполнять перестановку слагаемых, так как слагаемые, которые мы собираемся сгруппировать, итак находятся рядом. Нам нужно лишь заключить их в скобки, имеем (1+2)+3 . На этом группировка слагаемых завершена.

Разберем еще один пример. Возьмем числовое выражение 1+8+2+9 , представляющее собой сумму четырех слагаемых, и сгруппируем первое слагаемое с последним, а второе – с третьим. Для этого сначала переставляем слагаемые так, чтобы те слагаемые, которые мы собираемся сгруппировать, оказались рядом: 1+9+8+2 . Осталось заключить группируемые слагаемые в скобки (1+9)+(8+2) .

По озвученному правилу выполняется и группировка слагаемых в выражениях с переменными. Например, в сумме вида x+y 3 +3·y 2 +2·x 2 +y+1 можно сгруппировать все слагаемые с переменной x и все слагаемые с переменной y , после этого преобразования мы получим выражение (x+2·x 2 )+(y 3 +3·y 2 +y)+1 .

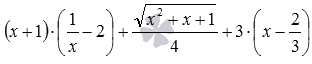
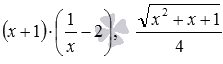
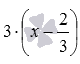
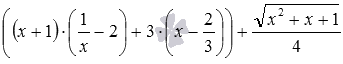
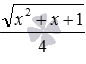
Следует заметить, что часто основные трудности с группировкой слагаемых заключаются не в самой группировке, а в том, чтобы разглядеть в исходном выражении сумму и составляющие ее слагаемые. Особенно это касается громоздких выражений. Когда слагаемые найдены, их группировка не вызывает проблем. Например, выражение представляет собой сумму трех слагаемых и . После того, как мы определили эти слагаемые, мы можем сгруппировать, например, первое слагаемое с третьим, при этом получим выражение . Кстати, в дроби под знаком корня находится сумма трех слагаемых, в которой тоже можно провести группировку.

Группировка слагаемых широко применяется для рационального вычисления значений выражений, при упрощении выражений и при решении многих других математических задач. К примеру, при вычислении значения выражения 1/3+2/7+2/3+3/7 удобно сгруппировать дроби с одинаковым знаменателем, что упрощает и ускоряет вычисления: 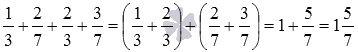. К слову, на группировке слагаемых базируется один из методов разложения многочлена на множители.

Группировка множителей, примеры

Группировка множителей по своему смыслу аналогична группировке слагаемых, только она проводится не в суммах, а в произведениях. Так под группировкой множителей в произведении понимают объединение нескольких множителей в группу.

Группировка множителей проводится по правилу, которое также аналогично правилу группировки слагаемых: группируемые множители переставляются в произведении так, чтобы они оказались рядом одно за другим, после чего они заключаются в скобки. Теоретической базой этого правила являются переместительное и сочетательное свойство умножения.

Для примера сгруппируем отдельно числовые и отдельно буквенные множители в произведении 3·a·7·b . Для этого сначала выполняем перестановку множителей, чтобы группируемые множители оказались рядом, имеем 3·7·a·b , после чего записываем скобки. В результате группировки множителей приходим к выражению вида (3·7)·(a·b) .

Источник

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник

Группировка слагаемых

Группировка слагаемых — это объединение слагаемых в группы с помощью скобок. При группировке слагаемых обычно изменяется порядок их следования в сумме для удобства вычислений.

Метод группировки слагаемых можно применять к суммам, состоящим из трёх и более слагаемых. Группировку можно разбить на три последовательных действия:

1. нахождение слагаемых, которые можно объединить в группу;
2. перестановка слагаемых (применение переместительного закона сложения);
3. заключение слагаемых в скобки (применение сочетательного закона сложения).

Рассмотрим нахождение значения выражения, изображённого на картинке:

Можно просто сначала сложить первые два слагаемых, к полученной сумме прибавить третье слагаемое, а к полученному результату затем прибавить четвёртое слагаемое:

15 + 27 + 55 + 13 = 42 + 55 + 13 = 97 + 13 = 110,

но в данном случае значение выражения будет легче найти, если сначала сгруппировать слагаемые так, чтобы в сумме они давали круглые числа:

15 + 27 + 55 + 13 = (15 + 55) + (27 + 13) = 70 + 40 = 110.

Приём группировки слагаемых обычно используется для упрощения вычислений.

Пример. Вычислить значение выражений, используя приём группировки слагаемых.

1) 248 + 123 + 52 + 7;

2) 101 + 67 + 19 + 3;

3) 340 + 114 + 60 + 26;

4) 154 + 235 + 13 + 115 + 46.

1) 248 + 123 + 52 + 7 = ( 248 + 52) + ( 123 + 7) = 300 + 130 = 430;

2) 101 + 67 + 19 + 3 = ( 101 + 19) + ( 67 + 3) = 120 + 70 = 190;

3) 340 + 114 + 60 + 26 = ( 340 + 60) + ( 114 + 26) = 400 + 140 = 540;

4) 154 + 235 + 13 + 115 + 46 = ( 154 + 46) + ( 235 + 115) + 13 = 200 + 350 + 13 = 563.

Источник

Что значит группировки слагаемых

Автор: Литвинова Александра Сергеевна

Организация: МОУ СШ №103

Населенный пункт: г. Волгоград

1. Литвинова Александра Сергеевна
2. Класс: 3 «Б»
3. Предмет: математика
4. Тема: «Группировка слагаемых»
5. Место и роль урока в изучаемой теме: урок изучения нового материала

Цель: создание условий для формирования умения выполнять группировку слагаемых.

Задачи:

• Образовательные: способствовать формированию умения выполнять группировку слагаемых.
• Развивающие: способствовать развитию совершенствования вычислительных навыков.
• Воспитательные: способствовать воспитанию чувства товарищества, аккуратности, усидчивости.

1. Дидактические средства:

Для учителя: средства ИКТ (презентация), проектор, компьютер, учебник, раздаточный материал.

Для учащихся: учебник, тетрадь.

1. Характеристика этапов урока:

Этапы урока

Содержание этапа

Деятельность учителя

Деятельность учащихся

Формы работы

УУД

1.

Мотивация (самоопределение) к учебной деятельности.

Настрой на предстоящую работу.

Здравствуйте ребята, присаживайтесь.

Меня зовут Александра Сергеевна.

Сегодня урок математики буду вести у вас я

Каждый день – всегда везде

На занятиях в игре

Смело четко говорим

И тихонечко сидим.

Откройте тетради. Запишите дату, классная работа.

Открывают тетрадь, записывают дату.

Регулятивные: самостоятельно организовывать своё рабочее место.

Личностные: овладевать мотивами учебной деятельности и личностным смыслом учения

2.

Актуализация и фиксирование индивидуального затруднения в проблемном действии.

— Начнем мы наш урок с небольшой разминки.

Заполните пропуски в таблице, выполняя вычисления.

мн 120 111 3 7 100

пр 300 896 900 700

Самопроверка по эталону.

Ребята, кто допустил 3 ошибка. Поднимите руку?

Кто не допустил ни одной ошибки?

Экспресс-опрос

-Как называется математическое действие, в котором используется знак +?

-Как называются числа при сложении?

-Как называется результат действия сложения?

Источник

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Источник