Что значит геометрии перпендикулярно

Перпендикулярность

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Смотреть что такое «Перпендикулярность» в других словарях:

ПЕРПЕНДИКУЛЯРНОСТЬ — (от сл. перпендикуляр). Отвесность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕРПЕНДИКУЛЯРНОСТЬ от слова перпендикуляр. Отвесность. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык,… … Словарь иностранных слов русского языка

перпендикулярность — вертикальность, нормальность, ортогональность Словарь русских синонимов. перпендикулярность сущ., кол во синонимов: 4 • вертикальность (3) • … Словарь синонимов

ПЕРПЕНДИКУЛЯРНОСТЬ — ПЕРПЕНДИКУЛЯРНОСТЬ, перпендикулярности, мн. нет, жен. (мат.). Перпендикулярное положение. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

перпендикулярность — ПЕРПЕНДИКУЛЯРНЫЙ, ая, ое; рен, рна. Являющийся перпендикуляром. Перпендикулярные линии. Расположить перпендикулярно (нареч.) к чему н. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Перпендикулярность — 4.16 Перпендикулярность: а) поверхности 6 к поверхностям 7 и 9; Источник: ГОСТ 2110 93: Станки расточные горизонтальные с крестовым столом. Нормы точности оригинал документа … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случай ортогональности. Содержание 1 На плоскости 1.1 Перпендикулярные … Википедия

Перпендикулярность — ж. Перпендикулярное положение, расположенность под прямым углом к чему либо. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

перпендикулярность — перпендикулярность, перпендикулярности, перпендикулярности, перпендикулярностей, перпендикулярности, перпендикулярностям, перпендикулярность, перпендикулярности, перпендикулярностью, перпендикулярностями, перпендикулярности, перпендикулярностях… … Формы слов

перпендикулярность — перпендикул ярность, и … Русский орфографический словарь

перпендикулярность — см. перпендикулярный; и; ж. Перпендикуля/рность плоскостей. Перпендикуля/рность расположения предметов … Словарь многих выражений

Источник

Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

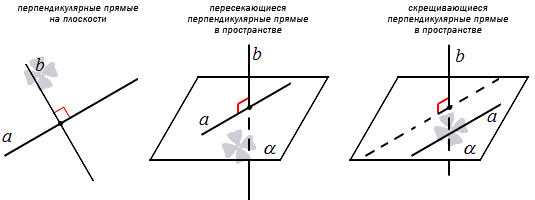
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается « ⊥ », а запись принимает вид a ⊥ b , что значит, прямая a перпендикулярна прямой b .

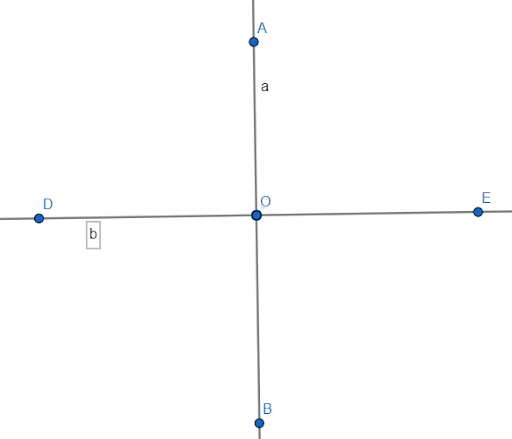
Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые O x , O z , O y перпендикулярны попарно: O x и O z , O x и O y , O y и O z .

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b .

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Пусть введена прямоугольная декартова система координат О х у с заданными уравнениями прямой на плоскости, которые определяют прямые a и b . Направляющие векторы прямых a и b обозначим a → и b → . Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a → и b → . Это возможно только при скалярном произведении векторов a → = ( a x , a y ) и b → = ( b x , b y ) равном нулю, а запись имеет вид a → , b → = a x · b x + a y · b y = 0 . Получим, что необходимым и достаточным условием перпендикулярности прямых a и b , находящихся в прямоугольной системе координат О х у на плоскости, является a → , b → = a x · b x + a y · b y = 0 , где a → = ( a x , a y ) и b → = b x , b y — это направляющие векторы прямых a и b .

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b .

Заданы три точки A ( 8 , 6 ) , B ( 6 , 3 ) , C ( 2 , 10 ) в прямоугольной системе координат О х у . Определить, прямые А В и А С перпендикулярны или нет.

Прямые А В и А С имеют направляющие векторы A B → и A C → соответственно. Для начала вычислим A B → = ( — 2 , — 3 ) , A C → = ( — 6 , 4 ) . Получим, что векторы A B → и A C → перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

A B → , A C → = ( — 2 ) · ( — 6 ) + ( — 3 ) · 4 = 0

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Определить, заданные прямые x — 1 2 = y — 7 3 и x = 1 + λ y = 2 — 2 · λ перпендикулярны или нет.

Решение

a → = ( 2 , 3 ) является направляющим вектором заданной прямой x — 1 2 = y — 7 3 ,

b → = ( 1 , — 2 ) является направляющим вектором прямой x = 1 + λ y = 2 — 2 · λ .

Перейдем к вычислению скалярного произведения векторов a → и b → . Выражение будет записано:

a → , b → = 2 · 1 + 3 · — 2 = 2 — 6 ≠ 0

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a → , b → = a x · b x + a y · b y + a z · b z = 0 , где a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x 2 = y — 1 = z + 1 0 и x = λ y = 1 + 2 · λ z = 4 · λ

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a → = ( 2 , — 1 , 0 ) и b → = ( 1 , 2 , 4 ) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a → , b → = 2 · 1 + ( — 1 ) · 2 + 0 · 4 = 0 .

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b , это и есть необходимое и достаточное условие.

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида A x + B y + C = 0 , уравнения прямой в отрезках вида x a + y b = 1 , уравнения прямой с угловым коэффициентом вида y = k x + b координаты векторов возможно найти.

Выяснить, перпендикулярны ли прямые 3 x — y + 2 = 0 и x 3 2 + y 1 2 = 1 .

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что n α → = ( 3 , — 1 ) — это нормальный вектор для прямой 3 x — y + 2 = 0 .

Упростим уравнение x 3 2 + y 1 2 = 1 до вида 2 3 x + 2 y — 1 = 0 . Теперь четко видны координаты нормального вектора, которые запишем в такой форме n b → = 2 3 , 2 .

Векторы n a → = ( 3 , — 1 ) и n b → = 2 3 , 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0 . Получим n a → , n b → = 3 · 2 3 + ( — 1 ) · 2 = 0 .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y = k 1 x + b 1 , а прямая b — y = k 2 x + b 2 , отсюда следует, что нормальные векторы будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) . Само условие перпендикулярности сводится к k 1 · k 2 + ( — 1 ) · ( — 1 ) = 0 ⇔ k 1 · k 2 = — 1 .

Выяснить, перпендикулярны ли прямые y = — 3 7 x и y = 7 3 x — 1 2 .

Прямая y = — 3 7 x имеет угловой коэффициент, равный — 3 7 , а прямая y = 7 3 x — 1 2 — 7 3 .

Произведение угловых коэффициентов дает значение — 1 , — 3 7 · 7 3 = — 1 , то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Определить, являются ли заданные прямые x — y — 1 = 0 и x 0 = y — 4 2 перпендикулярными.

Получаем, что нормальный вектор прямой x — y — 1 = 0 имеет координаты n a → = ( 1 , — 1 ) , а b → = ( 0 , 2 ) — направляющий вектор прямой x 0 = y — 4 2 .

Отсюда видно, что векторы n a → = ( 1 , — 1 ) и b → = ( 0 , 2 ) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t , чтобы выполнялось равенство n a → = t · b → . Отсюда вывод, что прямые не являются перпендикулярными.

Источник

Определение перпендикулярных прямых, их свойства, характеристика

Содержание:

В геометрии существует понятие параллельных и перпендикулярных прямых. Ко вторым относится особый вид пересечения простейших геометрических фигур. Рассмотрим, какие прямые называются перпендикулярными. После теоретической выкладки материала научим правильно чертить такие чертежи при помощи угольника. Также разберёмся, что такое перпендикуляр к прямой, его свойства, обозначение.

Перпендикулярные прямые: определение, свойства

Теперь вы понимаете, что значит перпендикулярные прямые.
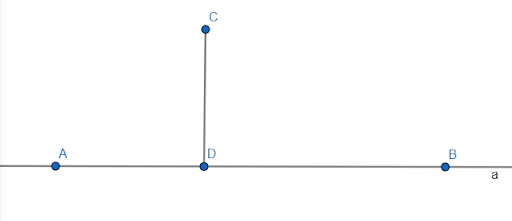
Дана линия a (AB) и не лежащая на ней точка C. Соединяющий их отрезок CD называется перпендикулярным, если отрезок CD образует с AB прямые углы. Точка D – основание перпендикуляра.

Способы построения

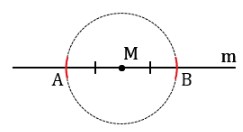
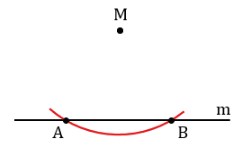
Второй способ сложнее. Дана линия m с лежащей на ней точкой M: M ∈ m. Построить отрезок PQ, проходящий через точку M и пересекающий m под прямым углом.

• Произвольно чертится линия (желательно горизонтально) m, на неё наносится точка M в произвольном месте.

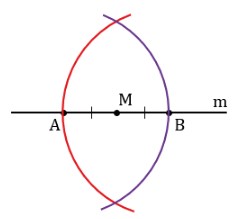
• Игла циркуля устанавливается в точку M, на лучах m ставится пара засечек на одинаковом расстоянии от M: это отрезки AM и MB, равные по длине.

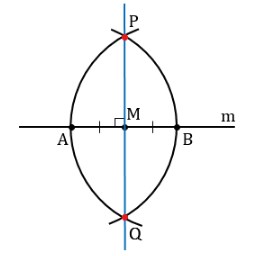
• Игла циркуля устанавливается последовательно в точки A и B, строятся дуги, приблизительно заканчивающиеся в точках, из которых к M будет опускаться перпендикуляр. Важно, чтобы части окружности пересеклись под и над m в точках P, Q.

• Через центр M проводится отрезок PQ, пересекающий прямую под углом 90°.

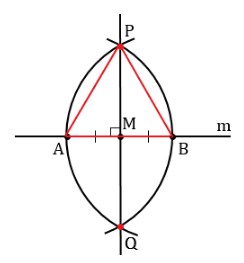
Теперь разберёмся, как доказать, что отрезки (прямые) перпендикулярны. Для этого рассмотрим треугольник APB или AQB (из условий задачи они одинаковые).

Две стороны простейшего многоугольника построены по радиусам одинаковых кругов, значит, они равны по длине – получаем равнобедренный треугольник, где AP = PB. Из условий задачи AM = BM, значит MP – медиана равнобедренного треугольника (исходя из определения этого термина). Отрезок PM – высота геометрической фигуры, она перпендикулярна основанию: PM ⟂ AB, что требовалось доказать.

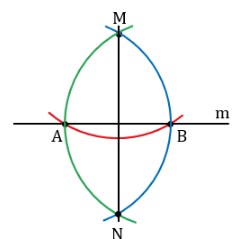
Проводим линию m и не лежащую на ней точку M. Рисуем окружность с центром M, пересекающую m в паре точек: A, B.

Чертим окружности с центрами в A и B, пересекающие M. Симметричную ей относительно прямой m точку обозначим N. Соединим их отрезком MN.

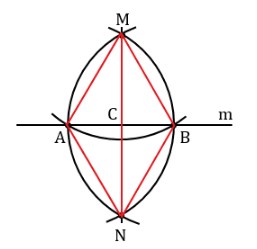
Докажем перпендикулярность MN линии m.

В треугольниках ANM с BNM равны стороны: AN = NB = AM = NB, AB – общая. Если три стороны треугольников равны, значит геометрические фигуры одинаковые: ∠АМС = ∠ВМС. Отрезки MC и CN – биссектрисы треугольников, где AB – основание. Далее, исходя из свойств равнобедренного треугольника, MC и CN – высоты геометрической фигуры, они перпендикулярны основанию. Получается, AB ⟂ MN.

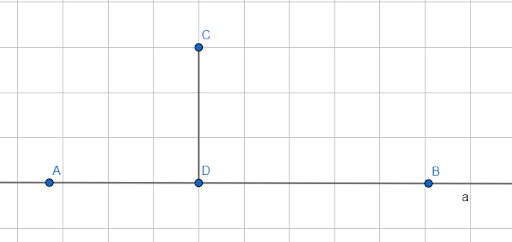
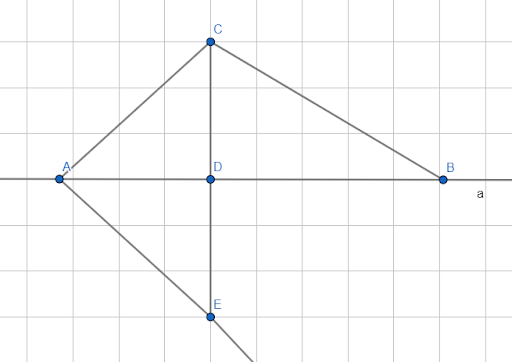
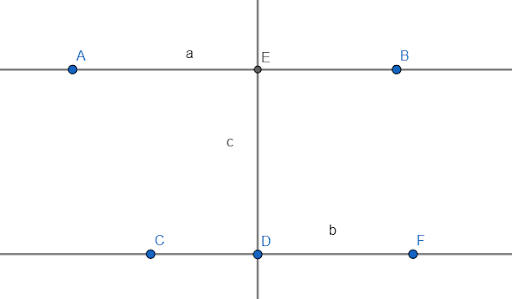
Задача

Мы доказали, что CE ⟂ a.
Последний шаг: покажем, что из точки C к прямой a нельзя провести более одного перпендикуляра.
Предположим: из точки С на прямую a возможно опустить второй перпендикуляр CD1. Тогда получим △CDD1 уже с парой прямых углов, что невозможно – у треугольника более одного прямого угла быть не может. Значит, из точки C нельзя опустить более одного перпендикуляра.
Исходя из рассмотренного материала, следует закономерное свойство двух прямых a и b, перпендикулярных к третьей c: между собой они параллельны: a||b.

Перпендикулярные отрезки – это отрезки, пересекающиеся под углом 90°.

Источник