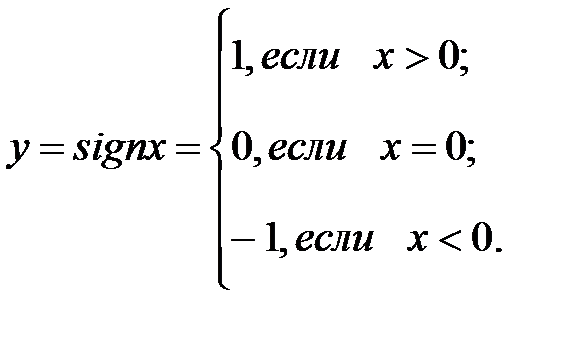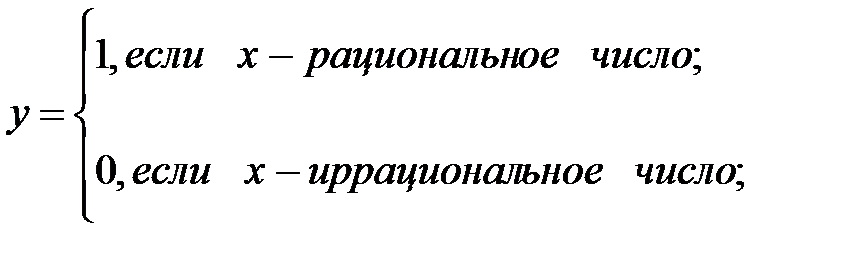Ограниченные сверху, снизу и ограниченные функции
Определение №1.Функция 
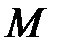
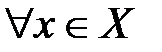
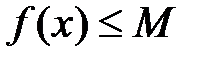
, определенная на некотором множестве 
, называется ограниченной сверху на этом множестве, если существует такое число 
, что для любого 
выполняется неравенство: 
.
Определение №2.Функция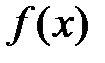 
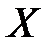
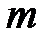
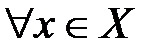
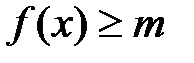
, определенная на некотором множестве 
, называется ограниченной снизу на этом множестве, если существует такое число 
, что для любого 
выполняется неравенство 
.
Определение №3. Функция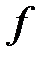 
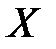
, ограниченная сверху и снизу на множестве , называется ограниченной на этом множестве.
Очевидно, что функция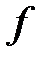 
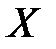
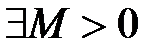
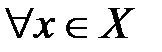
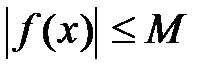
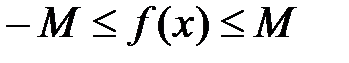
ограничена на множестве тогда, когда существует такое число 
, что для любого 
выполняется неравенство 
или 
.
Верхняя и нижняя грани функции
Определение №1.Верхняя грань множества значений 
числовой функции 
, определенной на множестве , называется верхней гранью функции . Обозначение: 
или 
.
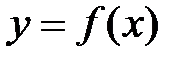
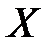
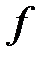
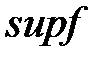
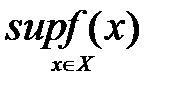
Определение №2. Нижняя грань множества значений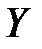 
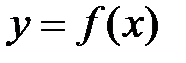
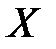
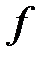
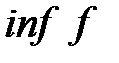
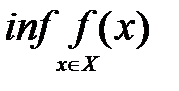
числовой функции 
, определенной на множестве , называется нижней гранью функции . Обозначение: 
или 
.
Замечание.1. Верхняя (нижняя) грань функции может быть как конечной, так и бесконечной.
2. Функция ограничена сверху (снизу) на множестве 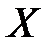тогда и только тогда, когда она имеет на этом множестве конечную верхнюю (нижнюю) грань.
Наибольшие, наименьшие, максимальные, минимальные и экстремальные значения функции
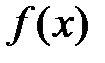
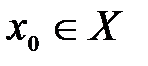
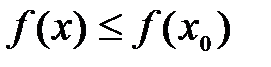
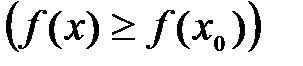
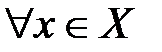
Определение №1.Функция , определенная на множестве , принимает в точке 
наибольшие (наименьшие) значения, если 
.
Определение №2.Наибольшие (наименьшие) значения функции называется также максимальным (минимальным) значением и пишется: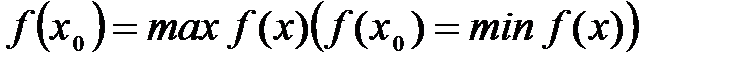 
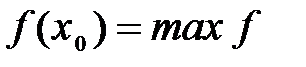
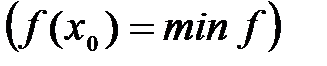
или 
.
Определение №3.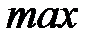 
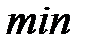
и 
значения функции называются экстремальными.
График функции
Определение №1.График функции – это множество пар точек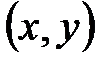 
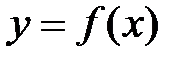
, координаты которых связаны соотношением 
.
Определение №2.Соотношение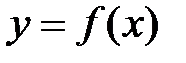 
называется уравнением графика функции.
Пример:График функции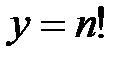 
состоит из отдельных точек (рис.1.).
| 8 4 |
| y4 |
| 1! |
| 2! |
| 3! |
| x |
| -1 |
| -1 |
| x1 |
| y1 |
| y2 |
| y |
| x |
Замечание. Не всякая линия является графиком какой-либо одной функции.
Пример.Уравнение окружности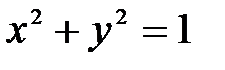 
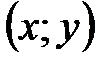
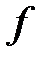
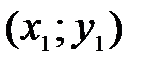
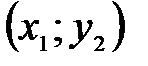
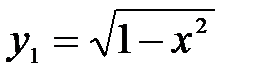
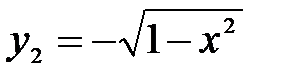
не является графиком одной функции, так как каждое 
входит не в одну, а в две пары чисел 
этого множества 
. 
и 
, где 
; 
.
А это противоречит требованию однозначности в определении функций. Но часть окружности, лежащая в нижней полуплоскости, является графиком функции 
. А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции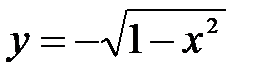 
.
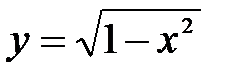
Способы задания функции
Определение.Задать функцию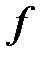 
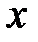
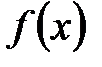
– это значит, указать, как по каждому значению аргумента 
найти соответствующие ему значения функции 
.
Существует три способа задания функции: аналитический, табличный и графический.
I. Аналитический явный способ задания функции
Сущность способа: Зависимость между переменными величинами определяется с помощью формулы. Она указывает, какие действия надо выполнить, чтобы получить значение функции, соответствующие данному значению аргумента.
Пример: Формула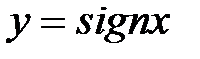 
(сигнум с латинского языка «знак») задает функцию 
| y |
| x |
| -1 |
Данная функция задана с помощью нескольких формул. Эта функция определена на всей числовой прямой. А множество ее значений состоит из –1;0;1.
2. Функция Дирихле 
определена на всей числовой прямой. А множество ее значений состоит из двух чисел: 1,0. Функцию Дирихле графически изобразить нельзя.
II. Аналитически неявный способ задания функции
1. Неявные функции
Определение.Пусть задано уравнение вида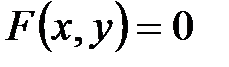 
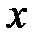
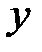
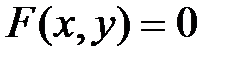
, т.е. задана функция двух действительных переменных 
и 
. Причем, рассматриваются только такие пары (если они существуют), для которых выполняется условие 
. Функции, задаваемые таким образом, называются неявными.
Замечание.1. Термин «неявная» отражает не характер функциональной зависимости, а лишь способ ее задания.
2. Одна и та же функция может быть задана как явно, так и неявно.
Пример: Функции, заданные явно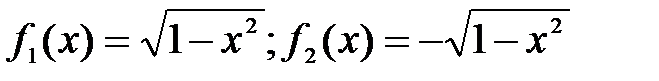 
могут быть заданы и неявным образом с помощью уравнения: 
.
3. Сложные функции
Если заданы функции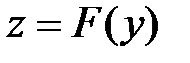 
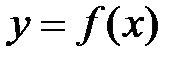
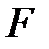
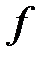
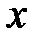
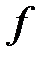
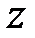
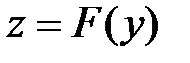
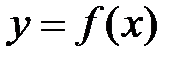
и 
, причем, область определения функции 
содержит множество значений функции , тогда каждому 
из области определения функции естественным образом соответствует 
такое, что 
, где 
.
Определение.Функция, определяемая соотношением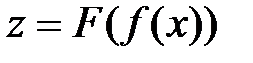 
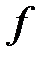
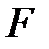
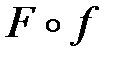
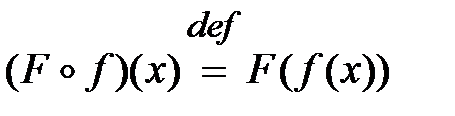
называется сложной функцией или, композицией функций или суперпозицией функций и и обозначается 
т.е.
.
Сложная функция отражает не характер функциональной зависимости, а лишь способ ее задания.
Пример.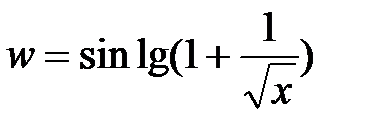 
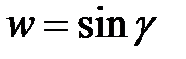
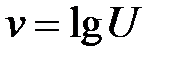
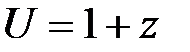
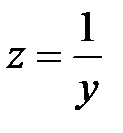
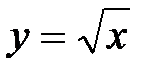
. Данную функцию можно рассматривать как суперпозицию следующих функций: 
; 
; 
; 
; 
.
III. Табличный способ задания функции
Пусть дана таблица
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| y | −1 |
Поставим в соответствие каждому значению 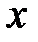, записанному в первой строке таблицы, число 
, стоящее во второй строке под числом . Тогда, можно сказать, что функция задана таблично. Областью определения этой функции является множество, состоящее из 8 чисел . Они перечислены в первой строке таблицы. Множеством значений этой функции является множества, состоящее из 8 чисел 
, перечисленных во второй строке. С помощью таблицы можно задать функцию только при конечном числе значений аргумента. Таблицы часто используются для задания функции.
Пример: Таблицы тригонометрических функций; таблицы логарифмов и т.д.
IV. Графический способ задания функции
Соответствие между переменными 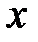и y задается посредством графика. Обычно графики чертятся с помощью самопишущих приборов. Данный способ задания функции используется при физических, медицинских измерениях.
Источник
