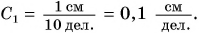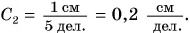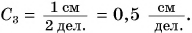Что значит если величина прямо измерена

Прямое измерение

Измерения как экспериментальные процессы весьма разнообразны. Это объясняется множеством экспериментальных величин, различным характером измерения величин, различными требованиями точности измерения и другие.

Наиболее распространена классификация видов измерений в зависимости от способа обработки экспериментальных данных. В соответствии с этой классификацией измерения делятся на прямые, косвенные, совместные и совокупные.

Содержание

Прямое измерение

Прямое измерение — это измерение, при котором искомое значение физической величины находится непосредственно из опытных данных в результате сравнения измеряемой величины с эталонами.

Косвенное измерение

Косвенное измерение — измерение, при котором искомое значение величины находится на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

• сопротивлениерезистора находим на основании закона Ома подстановкой значений силы тока и напряжения, получаемых в результате прямых измерений.

Совместное измерение

Совместное измерение — одновременное измерение нескольких неодноименных величин, для нахождения зависимости между ними. При этом решается система уравнений.

• определение зависимости сопротивления от температуры. При этом измеряются неодноименные величины, по результатам измерений определяется зависимость.

Совокупное измерение

Совокупное измерение — одновременное измерение нескольких одноименных величин, при котором искомые значения величин находятся решением системы уравнений, состоящих из результирующих прямых измерений различных сочетаний этих величин.

• измерение сопротивления резисторов, соединённых треугольником. При этом измеряется значение сопротивления между вершинами. По результатам определяются сопротивления резисторов.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Прямое измерение» в других словарях:

прямое измерение — Измерение, при котором искомое значение физической величины получают непосредственно. Примечание. Термин прямое измерение возник как противоположный термину косвенное измерение. Строго говоря, измерение всегда прямое и рассматривается как… … Справочник технического переводчика

прямое измерение — 3.5 прямое измерение (direct measurement): Измерение, посредством которого отдельные компоненты и/или группы компонентов определяются путем сравнения с идентичными компонентами в ГСО. Источник … Словарь-справочник терминов нормативно-технической документации

Прямое измерение — 19) прямое измерение измерение, при котором искомое значение величины получают непосредственно от средства измерений;. Источник: Федеральный закон от 26.06.2008 N 102 ФЗ (ред. от 28.07.2012) Об обеспечении единства измерений … Официальная терминология

прямое измерение — tiesioginis matavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Matuojamojo dydžio vertės nustatymas tiesiog iš eksperimento duomenų. pavyzdys( iai) Kūno masės matavimas skaitmeninėmis svarstyklėmis. atitikmenys: angl. direct… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

прямое измерение — tiesioginis matavimas statusas T sritis fizika atitikmenys: angl. direct measurement vok. direkte Messung, f rus. непосредственное измерение, n; прямое измерение, n pranc. mesure directe, f … Fizikos terminų žodynas

прямое измерение — tiesioginis matavimas statusas T sritis automatika atitikmenys: angl. direct measurement vok. direkte Messung, f; Direktmessung, f rus. прямое измерение, n pranc. mesurage direct, m; mesure directe, f … Automatikos terminų žodynas

Прямое измерение — 1. Измерение, при котором искомое значение величины получают непосредственно Употребляется в документе: ОСТ 45.159 2000 Отраслевая система обеспечения единства измерений. Термины и определения … Телекоммуникационный словарь

Измерение (физика) — Измерение совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением… … Википедия

Измерение — У этого термина существуют и другие значения, см. Измерение (значения). Измерение совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом… … Википедия

Измерение — [measurement] операция, посредством которой определяется отношение одной (измеряемой) величины к другой однородной величине (принимаемой за единицу); число, выражающее такое отношение, называется численным значением измеряемой величины.… … Энциклопедический словарь по металлургии

Источник

Метрология. Прямые и косвенные измерения.

Метрологией называется наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Измерением называется нахождение значения физической величины опытным путем с помощью специальных технических средств. Результатом измерения является количественная характеристика физической величины в виде числа единиц измеряемой величины и погрешность, с которой получено данное число.

Виды измерений. В зависимости от способа получения числового значения измеряемой величины измерения делятся на прямые, косвенные и совокупные измерения.

Прямыми называются измерения, при которых искомое значение величины получают из опытных данных. При прямых измерениях экспериментальные операции производятся над самой измеряемой величиной. Числовое значение измеряемой величины получают в экспериментальном сравнении с мерой или по показаниям приборов. Например, измерение тока амперметром, напряжения вольтметром, температуры термометром, массы на весах.

Косвенными называют такие измерения, при которых числовое значение измеряемой величины определяется по известной функциональной зависимости через другие величины, которые можно прямо измерить. При косвенных измерениях числовое значение измеряемой величины получают с участием оператора на основе прямых измерений – решением одного уравнения. К косвенным измерениям прибегают в тех случаях, когда неудобно или невозможно осуществить автоматическое вычисление известной зависимости между одной или несколькими входными величинами и измеряемой величиной. Например, мощность в цепях постоянного тока определяет оператор, умножая напряжение на ток, измеренные прямым измерением с помощью амперметра и вольтметра.

Отклонение результата измерения от истинного значения измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения равна разности между результатом измерения и истинным значением измеряемой величины : .

Относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к истинному значению измеряемой величины. Обычно относительная погрешность выражается в процентах %.

25. Основные понятия и определения: информация, алгоритм, программа, команда, данные, технические устройства.

Информация — от латинского слова «information», что означает сведения, разъяснения, изложение.

Применительно к компьютерной обработке данных под информацией понимают некоторую последовательность символических обозначений (букв, цифр, закодированных графических образов и звуков и т.п.), несущую смысловую нагрузку и представленную в понятном компьютеру виде. Каждый новый символ в такой последовательности символов увеличивает информационный объём сообщения.

Алгоритм — последовательность чётко определенных действий, выполнение которых ведёт к решению задачи. Алгоритм, записанный на языке машины, есть программа решения задачи.

Свойства алгоритмов: дискретность, понятность, результативность, определенность, массовость.

Программа — последовательность действий, инструкций, предписаний для некоторого вычислительного устройства; файл, содержащий эту последовательность действий.

Команда — это указание компьютерной программе действовать как некий интерпретатор для решения задачи. В более общем случае, команда — это указание некоему интерфейсу командной строки.

Данные — информация, представленная в формализованном виде, что обеспечивает возможность ее хранения, обработки и передачи.

Технические устройства (средства информатизации) – это совокупность систем, машин, приборов, механизмов, устройств и прочих видов оборудования, предназначенных для автоматизации различных технологических процессов информатики, причем таких, выходным продуктом которых является именно информация (сведения, знания) или данные, используемые для удовлетворения информационных потребностей в разных областях предметной деятельности общества.

Все технические средства информатизации в зависимости от выполняемых функций можно разделить на шесть групп : устройства ввода информации, устройства вывода информации, устройства обработки информации, устройства передачи и приема информации, устройства хранения информации, многофункциональные устройства.

Источник

Точность измерений и погрешности в физике — определение и формулы с примерами

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):

(5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины: и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

• Для линейки 1:
• Для линейки 2:
• Для линейки 3:

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Определение площади и объема
• Связь физики с другими науками
• Макромир, мегамир и микромир в физике
• Пространство и время
• Как зарождалась физика
• Единая физическая картина мира
• Физика и научно-технический прогресс
• Физические величины и их единицы измерения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник