Действия с конденсатором



9. Емкость плоского конденсатора С1 = 10 -10 Ф. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U1 = 600 В и отключили от источника. Какую работу необходимо совершить, чтобы вынуть диэлектрик из конденсатора? Трением пренебречь.
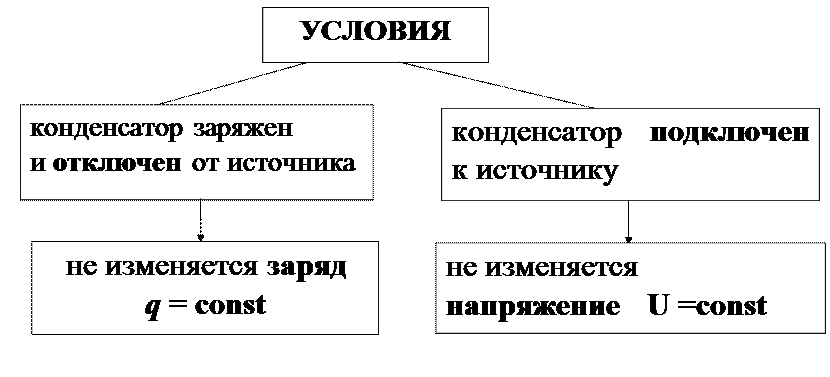
Если конденсатор отключили от источника, то напряжение уменьшается, но остается q = const.Энергия конденсатора: 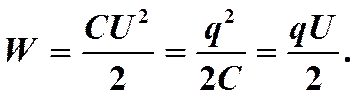
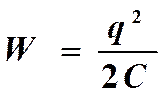
.
Если конденсатор остается подключенным к источнику, то q ≠ const, а
U = const = q1/C1 = q2/C2и W = ½ (CU 2 ).
10.Плоский конденсатор электроемкостью 4нФ подсоединен к источнику напряжения 10 В. Затем, не отключая конденсатор от источника, расстояние между его обкладками увеличили в 2 раза.
1) Найти, во сколько раз изменились следующие величины: а) электроемкость конденсатора, б) заряд на его обкладках, в) напряжение на конденсаторе, г) поверхностная плотность заряда, д) напряженность электростатического поля, е) поток Е через пластину конденсатора,
ж) электрическая индукция D, з) плотность энергии электрического поля в конденсаторе,
и) энергия конденсатора.
2) Рассчитать работу, затраченную на изменение расстояния между обкладками.
3) Найти заряд, прошедший через источник.
1) а) 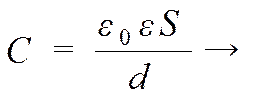
в) Т.к. конденсатор от источника не отключается, то U2 = U1 = U =10 B, но изменяется заряд:
г) 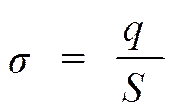
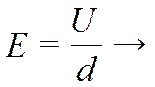
е)NE = ES , NE2 / NE1 = ½. ж) 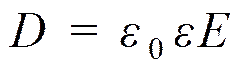
и)Когда U = const, то W = ½CU 2 ,
2) Работа внешних сил, затраченная на изменение расстояние между обкладками, рассчитывается как изменение энергии конденсатора:
3) Найдем заряд, прошедший через источник:
Источник
35. Электродинамика  Читать 0 мин.
Читать 0 мин.
35.441. Цепи
Через конденсатор постоянный ток не течёт.
Напряжение на параллельных участках цепи одинаково.
В системе отключенных конденсаторов заряд всегда остаётся постоянным. Напряжение и ёмкость может меняться.
Выделившееся количество теплоты равно разности начальной и конечной энергии:
Eн ― начальная энергия системы [Дж];
Ек ― конечная энергия системы [Дж].
Начальные и конечные энергии определяются энергиями конденсаторов и катушек индуктивности входящих в цепь.
После установления равновесия, напряжение есть только на конденсаторах, не подключенных параллельно к резисторам.
Конденсатор в цепи постоянного тока
Плоский конденсатор представляет собой пластинки, на которых может скапливаться заряд. Между пластинками находится пространство, заполненное диэлектриком (или воздухом в роли диэлектрика). Поскольку диэлектрики ― вещества, плохо проводящие ток, от одной пластины конденсатора через слой диэлектрика на другую пластину заряд перейти не может, а значит, через конденсатор ток не проходит. Если на участке цепи находится такой конденсатор ― этот участок «заблокирован», тока в нем нет.
Если на участке цепи находится конденсатор не заряженный, или заряженный частично, а цепь подключают к источнику тока ― на обкладках конденсатора начинает скапливаться заряд. Это означает, что на этом участке цепи до конденсатора есть ток ― до тех пор, пока конденсатор не заряжен полностью.
Если цепь от источника тока отключить, и в ней есть заряженный конденсатор ― конденсатор начинает разряжаться. Заряды с одной обкладки конденсатора пытаются перейти на другую, по «длинному пути» ― через всю цепь, создавая, таким образом, ток. Ток в такой цепи будет до тех пор, пока конденсатор не разрядится.
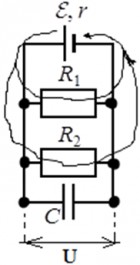
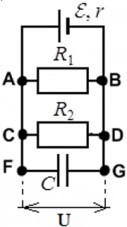
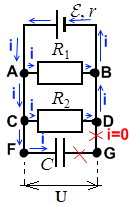
Пример: Пусть в цепи есть два резистора с сопротивлениями R1 и R2, источник ЭДС ε, и конденсатор емкостью C:
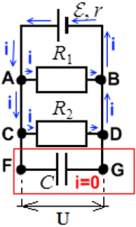
Конденсатор C полностью заряжен. В этом случае токи в цепи не проходят через участок цепи FG ― его словно нет в цепи, и в расчетах параметров цепи он не учитывается. Ток считается выходящим из положительно заряженной клеммы источника ЭДС (тонкая и длинная) к входящим в отрицательно заряженную клемму (жирная короткая черта):
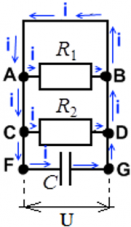
Конденсатор разряжен или заряжен не док конца. В этом случае конденсатор только заряжается, и ток в цепи через точку F проходит — вплоть до обкладки конденсатора – но дальше, в точку G ток не проходит.
Конденсатор заряжен, но от источника ЭДС цепь отключена. В этом случае ток идет через всю цепь ― пока конденсатор может служить источником зарядов и пока полностью не разрядится. Когда конденсатор разрядится ― ток в цепи прекратится.
Напряжения на всех параллельных участках цепи равны ― это основное свойство параллельного подключения. Вне зависимости от того, находится на ветви резистор, или конденсатор. Таким образом, во всех случаях для примера выше, напряжение на конденсаторе C равно напряжению на резисторе R1, и равно напряжению на резисторе R2. Благодаря этому свойству, зная, например, энергию, скопившуюся на заряженном конденсаторе, или его заряд, можно вычислить напряжение на резисторах.
Заряженный конденсатор, отключенный от цепи. У заряженного конденсатора на обкладках находится определенное количество заряда. Если конденсатор отключить от цепи ― заряду некуда переместиться, и он остается на конденсаторе неизменным. Получить дополнительный заряд, если он заряжен не до конца, конденсатору тоже неоткуда. Заряд конденсатора, отключенного от цепи, постоянен.
Электроемкость конденсатора ― это его физико-геометрическая характеристика, показывающая, как много заряда он может скопить. Электроемкость конденсатор не зависит ни от заряда на его обкладках, ни от напряжения в цепи.
Электроемкость конденсатора равна C = $\frac <\varphi_2 - \varphi_1>= \frac
$ , где
C ― электроемкость конденсатора, [Ф];
(φ2 – φ1) ― разность потенциалов на обкладках конденсатора, [В];
U ― напряжение на обкладках конденсатора [В].
Электроемкость плоского конденсатора зависит от размеров его пластин, расстояния между ними, а также типа диэлектрика, который заполняет пространство между пластинами.
Электроемкость плоского конденсатора равна C = $\frac<\varepsilon\varepsilon_0 S>
C ― ёмкость конденсатора [Ф];
ε ― диэлектрическая проницаемость;
ε0 ― электрическая постоянная;
S ― площадь обкладок конденсатора [м2];
d ― расстояние между обкладками [м].
В электрической цепи за счет сопротивления, которое преодолевают движущиеся в материале заряды, выделяется тепло. Количество теплоты, которая выделяется в цепи, равно разности начальной и конечной энергии всей системы Q = Eн – Eк¸ где
Eн ― начальная энергия системы [Дж];
Eк ― конечная энергия системы [Дж].
В цепи энергия скапливается на конденсаторах (энергия электрического поля) и на катушках индуктивности (энергия магнитного поля). Поэтому энергия электромагнитных сил в цепи в любой момент равна сумме энергий на конденсаторах и на катушках, которые входят в цепь.
Энергия электрического поля заряженного конденсатора равна We = $\frac
We ― энергия электрического поля конденсатора, [Дж];
C ― электроемкость конденсатора, [Ф];
U ― напряжение на обкладках конденсатора, [В];
q ― заряд на обкладках конденсатора, [Кл].
Энергия магнитного поля катушки индуктивности равна E = $\frac
E ― энергия магнитного поля катушки [Дж];
L ― индуктивность катушки [Гн];
I ― сила тока в катушке [А].
Состояние равновесия и зарядка конденсаторов
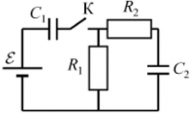
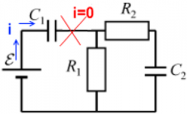
Пример 1: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, оба конденсатора емкостями C1 и C2 разряжены.
Ток от источника ЭДС до конденсатора C1 будет идти до тех пор, пока конденсатор C1 не будет полностью заряжен. При этом от конденсатора C1 дальше заряды не проходят ― ни на резисторы R1 и R2, ни на конденсаторC2. Как только конденсатор C1 полностью заряжается, в системе наступает состояние равновесия ― напряжение на конденсаторе становится равным ЭДС, весь возможный заряд конденсатор принял. Поскольку ток через него не прошел до конденсатора C2 ― этот конденсатор так и остался незаряженным. Напряжение есть лишь на конденсаторе C1, а на конденсаторе C2напряжение равно нулю. Зарядка конденсатораC1:
После того, как конденсатор C1 заряжен, ток в цепи прекращается.
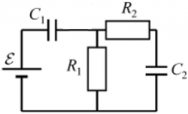
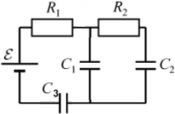
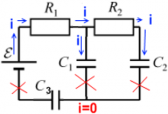
Пример 2: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, все три конденсатора емкостями C1, C2 и C3 разряжены.
Ток, выходя из источника ЭДС, разделяется на два тока ― один питает подзарядку конденсатораC1, а другой ― конденсатораC2. Состояние равновесия наступает, когда оба конденсатора полностью заряжены ― в цепи ток больше не проходит. Но так как ток дальше конденсаторов не проходит ― конденсатор C3 не получает заряд, и остается разряженным. Напряжение на конденсаторе C3 равно нулю.
Зарядка конденсаторов C1 иC2:
После того, как конденсаторыC1 и C2 заряжены, ток в цепи прекращается.
Источник
Зарядка и разрядка конденсатора
Пишу для школьников (для лучшего понимания ими основ физики). Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений.
Основной характеристикой конденсатора является его электрическая ёмкость С .
Под ёмкостью конденсатора понимается его способность накопить на своих обкладках и удержать на них электрический заряд.
Чем больший электрический заряд соберёт на себе конденсатор, тем больший заряд при разряде он отдаст во внешнюю электрическую цепь.
Ёмкость плоского конденсатора тем больше, чем больше площадь его пластин, чем меньше расстояние между ними и чем больше диэлектрическая проницаемость диэлектрика между его обкладками (объяснение дано в Занятии 53 ):
На практике конденсатор заряжают, присоединив его обкладки к полюсам источника постоянного напряжения.
Как происходит процесс зарядки конденсатора?
До зарядки каждая обкладка конденсатора имела одинаково е количество положительных и отрицательных зарядов, то есть не была заряжена.
Чтобы зарядить конденсатор надо, чтобы какое-то количество свободных электронов перешло с одной обкладки на другую. Поэтому обкладки и получают одинаковые по модулю, но противоположные по знаку заряды.
Вдумаемся в смысл слов:
- чтобы зарядить конденсатор, надо разъединит ь заряды;
- чтобы разрядить конденсатор, надо соединить разъединённые заряды.
Проведём мысленный эксперимент.
Имеются две металлические пластинки . Каждая из них не заряжена . Это значит, что в них содержится одинаковое количество положительных и отрицательных зарядов.
Перемещаться в металле могут только свободные (оторвавшиеся от атомов валентные) электроны.
Представим, что эти пластинки привели в очень тесное соприкосновение, при котором часть свободных электронов перешла, например, с верхней пластинки на нижнюю.
Тогда на поверхности верхней пластинки появится положительный заряд (там будет недостаток электронов). Поверхность же нижней пластинки зарядится отрицательно (на ней избыток электронов).
Пластинки, имеющие противоположные знаки, притягиваются друг к другу. Чтобы их разъединить, надо совершить механическую работу против силы притяжения.
После перемещения пластинок на некоторое расстояние друг от друга (после совершения механической работы), они окажутся заряженными разноимёнными равными по модулю зарядами.
Совершив работу, мы разделили заряды и зарядили пластинки. Совершённая механическая работа перешла в энергию электрического поля, образовавшегося между пластинками, которые можно считать обкладками плоского конденсатора.
Рассуждая так, мы представили процесс зарядки конденсатора.
Теперь представим процесс разрядки конденсатора.
Чтобы разрядить конденсатор, надо соединить разъединённые заряды, то есть вернуть электроны, перешедшие с верхней пластинки на нижнюю, на верхнюю пластинку. Тогда обе пластинки опять окажутся незаряженными.
Для этого надо заряженные пластинки соединить проводом. Тогда свободные электроны с отрицательно заряженной пластинки, отталкиваясь от неё, станут перемещаться в ближайший к пластинке участок провода. В результате заряд отрицательно заряженной пластинки уменьшается.
Количество электронов в этом участке провода ( прилегающего к отрицательно заряженной пластинке) увеличится . Эти электроны передадут движение (энергию) электронам соседнего участка провода и так далее.
Одновременно с другого конца провода, соединённого с положительно заряженной пластинкой, свободные электроны переходят на пластинку , уменьшая её положительный заряд . Направленное движение электронов и здесь передаётся от участка к участку провода.
Перераспределение электронов от участка к участку в проводе (электрический ток) происходит до тех пор, пока количество положительных и отрицательных зарядов в каждой пластинке не станет одинаковым ( пока разъединённые при зарядке пластин заряды не соединятся).
Процесс разрядки конденсатора — это процесс соединения разъединённых зарядов .
Так можно представить процессы зарядки и разрядки конденсатора.
Теперь рассмотрим качественно процесс зарядки конденсатора от источника постоянного тока.
Источник



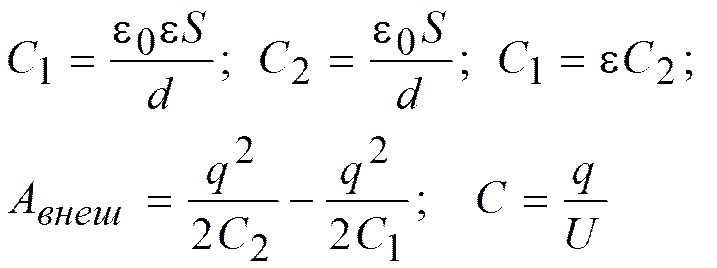
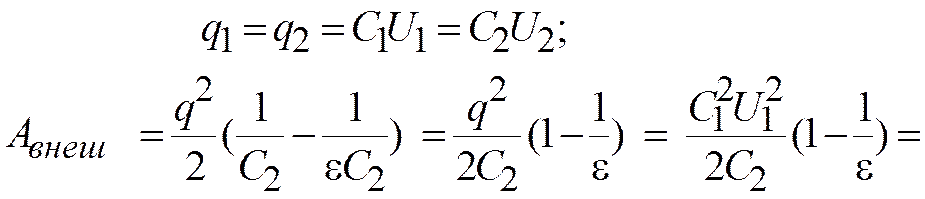

 Читать 0 мин.
Читать 0 мин.