- Значение слова эллипсоид
- эллипсоид в словаре кроссвордиста
- Толковый словарь русского языка. Д.Н. Ушаков
- Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
- Энциклопедический словарь, 1998 г.
- Имена, названия, словосочетания и фразы содержащие «эллипсоид»:
- Большая Советская Энциклопедия
- Имена, названия, словосочетания и фразы содержащие «эллипсоид»:
- Википедия
- Имена, названия, словосочетания и фразы содержащие «эллипсоид»:
- Примеры употребления слова эллипсоид в литературе.
- Эллипсоид
- Литература
- Полезное
- Смотреть что такое «Эллипсоид» в других словарях:
- Эллипсоид
- Из Википедии — свободной энциклопедии
- Эллипсоид — Ellipsoid
- СОДЕРЖАНИЕ
- Стандартное уравнение
- Параметризация
- Объем
- Площадь поверхности
- Примерная формула
- Плоские секции
- Характеристики
- Определение эллипса плоского сечения
- Штифтовая конструкция
- Этапы строительства
- Полуоси
- Converse
- Конфокальные эллипсоиды
- Предельный случай, эллипсоид вращения
- Свойства фокальной гиперболы
- Свойство фокального эллипса
- В общем положении
- Как квадрика
- Параметрическое представление
- Приложения
- Динамические свойства
- Динамика жидкостей
- По вероятности и статистике
- В высших измерениях
Значение слова эллипсоид
эллипсоид в словаре кроссвордиста
эллипсоид
Толковый словарь русского языка. Д.Н. Ушаков
эллипсоида, м. (мат.). Яйцевидное шарообразное тело получающееся при вращении эллипса вокруг одной из своих осей.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
м. Поверхность, образуемая вращением эллипса вокруг одной из своих осей.
Энциклопедический словарь, 1998 г.
замкнутая поверхность (2-го порядка). Эллипсоид можно получить из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях (рис.). Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения.
Имена, названия, словосочетания и фразы содержащие «эллипсоид»:
Большая Советская Энциклопедия
(от эллипс и греч. eidos ≈ вид), замкнутая центральная поверхность второго порядка . Э. имеет центр симметрии О (см. рис.) и три оси симметрии, которые называются осями Э. Точки пересечения координатных осей с Э. называются его вершинами. Сечения Э. плоскостями являются эллипсами (в частности, всегда можно указать круговые сечения Э.). В надлежащей системе координат уравнение Э. имеет вид:
Имена, названия, словосочетания и фразы содержащие «эллипсоид»:
Википедия
Имена, названия, словосочетания и фразы содержащие «эллипсоид»:
Примеры употребления слова эллипсоид в литературе.
А нам это существо представляется то шаром, то вытянутым извивающимся эллипсоидом вращения, то колеблющейся вереницей разнокалиберных сфер.
Земля не шар и — несмотря на близость вычислений Ньютона к реальности — не эллипсоид, а особое тело вращения, названное за отсутствием иных аналогий геоидом, т.
Корень, если можно было его так назвать, был едва заметен в лучах интравизоров — маленькая трехметровая опухоль в дне километрового эллипсоида, но опухоль эта постепенно прогрессировала, росла и спустя месяц достигла шестидесяти метров, привлекая к себе пристальное внимание ученых.
Давно уже переставший быть полусферой купол, пройдя стадии гиперболоида и параболоида, превратился в половину эллипсоида вращения, и эллипсоид этот все вытягивался.
Сенсоры зонда показывали, что до него не менее семисот пятидесяти километров, однако даже с этого расстояния, многократно увеличенный телекамерами он выглядел просто до неприличия большим — огромный эллипсоид не менее чем километрового диаметра, установить более точные размеры было сложно — подводить зонд слишком близко Дик опасался — еще примут за ракету и собьют, останешься потом без глаз и ушей.
В хрустальном эллипсоиде на высоте семи метров над полотном дороги сидели в креслах два машиниста, разделенные высоким пирамидальным колпаком электронного водителя-робота.
Вскоре, бешено вращаясь, гигантский решетчатый шар прототипа раскалился докрасна, вытянулся сначала в эллипсоид, а затем в узкое веретено, исчезнувшее в облаке раскаленных газов, втягиваемых в бездонную яму черной дыры.
Более половины огромного желтого пятна занимала черная тень Луны, которая несомненно приняла форму удлиняющегося эллипсоида.
Продолжив дело и ожидая результатов, Джек достал из шкатулки небольшой вибромолот и стал осторожно оббивать камень вокруг чужеродного включения, пока в кремне не появилась трещина и не открыла гладкий желтый эллипсоид в полдюйма длиной.
Источник: библиотека Максима Мошкова
Транслитерация: ellipsoid
Задом наперед читается как: диоспиллэ
Эллипсоид состоит из 9 букв
Источник
Эллипсоид
Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:


Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.
В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.
Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли.
Площадь поверхности эллипсоида вращения:
Литература
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр / интерактивный компьютерный учебник.
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Эллипсоид» в других словарях:
Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь
ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка
эллипсоид — а, м. ellipsoïde m. спец. Поверхность, образуемая вращением эллипса вокруг одной из своих осей. БАС 1. Глобусы в виде шара, груши, элипсоида. Кукольник Примеч. // К. 1851 1 556. Гало. Это эллипсоид диаметром более 600 тысяч световых лет,… … Исторический словарь галлицизмов русского языка
Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия
эллипсоид — сущ., кол во синонимов: 5 • безгранник (2) • коноид (4) • референц эллипсоид (2) … Словарь синонимов
ЭЛЛИПСОИД — ЭЛЛИПСОИД, эллипсоида, муж. (мат.). Яйцевидное шарообразное тело, получающееся при вращении эллипса вокруг одной из своих осей. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
эллипсоид — а; м. [от греч. elleipsis выпадение, опущение и eidos вид] Матем. Поверхность, образуемая вращением эллипса (1.Э.; 1 зн.) вокруг одной из своих осей. ◁ Эллипсоидный, ая, ое. * * * эллипсоид замкнутая поверхность (2 го порядка). Эллипсоид можно… … Энциклопедический словарь
Эллипсоид — [ellipsoid] замкнутая центральная поверхность 2 го порядка. Эллипсоид имеет центр симметрии и три оси симметрии, которые называются осями эллипсоида: Смотри также: эллипсоид деформации эллипсоид напряжений … Энциклопедический словарь по металлургии
эллипсоид — 3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси. Примечание Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.… … Словарь-справочник терминов нормативно-технической документации
ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь
Источник
Эллипсоид
Из Википедии — свободной энциклопедии
Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 , <\displaystyle <\frac 

Величины a, b, c называют полуосями эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.
В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.
Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли.
Параметрическое уравнение эллипсоида
x = a sin ( θ ) cos ( φ ) , y = b sin ( θ ) sin ( φ ) , z = c cos ( θ ) , <\displaystyle <\begin
0 ≤ θ ≤ π , 0 ≤ φ 2 π . <\displaystyle 0\leq \theta \leq \pi ,\qquad 0\leq \varphi
Площадь поверхности эллипсоида вращения [ источник не указан 3059 дней ] :
S = 4 π b 2 ( 1 + 2 3 e 2 + 3 5 e 4 + 4 7 e 6 + . . . + k + 1 2 k + 1 e 2 k + . . . ) . <\displaystyle S=4\pi b^<2>\left(1+<\frac <2><3>>e^<2>+<\frac <3><5>>e^<4>+<\frac <4><7>>e^<6>+. +<\frac
Oblate, prolate — сплюснутый и вытянутый соответственно.
Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Объём эллипсоида:
V = 4 3 π a b c . <\displaystyle V=<\frac <4><3>>\pi abc.>
Источник
Эллипсоид — Ellipsoid
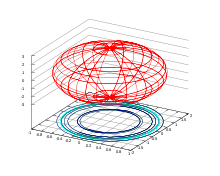
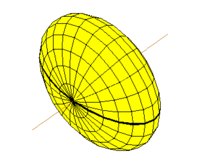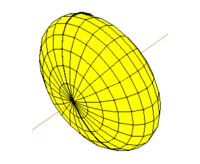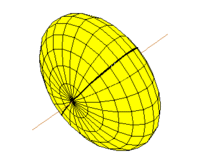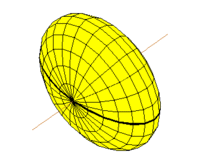
- Сфера , a = b = c = 4 ; Топ
- Сфероид , a = b = 5 , c = 3 ; внизу слева ,
- Трехосный эллипсоид, a = 4,5 , b = 6 ; c = 3 , внизу справа
Эллипсоида является поверхностью , которая может быть получена из сферы путем деформации его при помощи направленных скейлингов , или в более общем случае , из аффинного преобразования .
Эллипсоид — это квадратичная поверхность ; то есть поверхность , которая может быть определена как нулевое множество о наличии полинома степени два в трех переменная. Среди квадратичных поверхностей эллипсоид характеризуется одним из двух следующих свойств. Каждое плоское поперечное сечение представляет собой либо эллипс , либо пусто, либо сводится к одной точке (это объясняет название, означающее «подобный эллипсу»). Он ограничен , а значит, может быть заключен в достаточно большую сферу.
Эллипсоид имеет три попарно перпендикулярные оси симметрии, которые пересекаются в центре симметрии , называемом центром эллипсоида. Эти отрезки , которые разделяются на оси симметрии по эллипсоида называются главными осями , или просто осей эллипсоида. Если три оси имеют разную длину, эллипсоид называется трехосным или редко разносторонним , а оси определены однозначно.
Если две оси имеют одинаковую длину, то эллипсоид представляет собой эллипсоид вращения , также называемый сфероидом . В этом случае эллипсоид инвариантен относительно вращения вокруг третьей оси, поэтому существует бесконечное множество способов выбора двух перпендикулярных осей одинаковой длины. Если третья ось короче, эллипсоид представляет собой сплюснутый сфероид ; если длиннее, то это вытянутый сфероид . Если три оси имеют одинаковую длину, эллипсоид представляет собой сферу.
СОДЕРЖАНИЕ
Стандартное уравнение
Используя декартову систему координат, в которой начало координат является центром эллипсоида, а оси координат являются осями эллипсоида, неявное уравнение эллипсоида имеет стандартную форму
Икс 2 а 2 + у 2 б 2 + z 2 c 2 знак равно 1 , <\ displaystyle <\ frac
Точки ( a , 0, 0) , (0, b , 0) и (0, 0, c ) лежат на поверхности. Отрезки от начала координат до этих точек называются главными полуосями эллипсоида, потому что a , b , c составляют половину длины главных осей. Они соответствуют большой полуоси и малой полуоси в качестве эллипса .
Параметризация
Эллипсоид можно параметризовать несколькими способами, которые проще выразить, когда оси эллипсоида совпадают с осями координат. Обычный выбор
Икс знак равно а грех ( θ ) потому что ( φ ) , у знак равно б грех ( θ ) грех ( φ ) , z знак равно c потому что ( θ ) , <\ Displaystyle <\ begin <выровнен>Икс & = а \ грех (\ тета) \ соз (\ varphi), \\ у & = Ь \ грех (\ тета) \ грех (\ varphi), \\ z & = с \ соз (\ тета), \ конец <выровнено>> \, \!>
0 ≤ θ ≤ π , 0 ≤ φ 2 π . <\ displaystyle 0 \ leq \ theta \ leq \ pi, \ qquad 0 \ leq \ varphi
Эти параметры можно интерпретировать как сферические координаты , где θ — полярный угол, а φ — азимутальный угол точки ( x , y , z ) эллипсоида.
Измерение от центра, а не от полюса,
Икс знак равно а потому что ( θ ) потому что ( λ ) , у знак равно б потому что ( θ ) грех ( λ ) , z знак равно c грех ( θ ) , <\ Displaystyle <\ begin
— π 2 ≤ θ ≤ π 2 , 0 ≤ λ 2 π , <\ displaystyle - <\ tfrac <\ pi><2>> \ leq \ theta \ leq <\ tfrac <\ pi><2>>, \ qquad 0 \ leq \ lambda
Измерение углов непосредственно к поверхности эллипсоида, а не к описанной сфере,
[ Икс у z ] знак равно р [ потому что ( γ ) потому что ( λ ) потому что ( γ ) грех ( λ ) грех ( γ ) ] <\ Displaystyle <\ begin
р знак равно а б c c 2 ( б 2 потому что 2 λ + а 2 грех 2 λ ) потому что 2 γ + а 2 б 2 грех 2 γ , — π 2 ≤ γ ≤ π 2 , 0 ≤ λ 2 π . <\ displaystyle <\ begin
γ будет геоцентрической широтой на Земле, а λ — долготой. Это истинные сферические координаты с началом в центре эллипсоида.
В геодезии , то геодезическая широта наиболее часто используются, как угол между вертикальным и экваториальной плоскостью, определенным для двухосного эллипсоида. Для более общего трехосного эллипсоида см эллипсоидальную широту .
Объем
V знак равно 4 3 π а б c . <\ displaystyle V = <\ tfrac <4><3>> \ pi abc.>
В терминах главных диаметров A , B , C (где A = 2 a , B = 2 b , C = 2 c ) объем равен
V знак равно π 6 А B C <\ Displaystyle V = <\ tfrac <\ pi><6>> ABC> 
Это уравнение сводится к уравнению объема сферы, когда все три эллиптических радиуса равны, и к уравнению сплющенного или вытянутого сфероида, когда два из них равны.
Объем эллипсоида является 2 / 3 объем описанного эллиптического цилиндра , и π / 6 объем описанной коробки. В объемах этих вписанные и разграниченные коробки соответственно:
V вписанный знак равно 8 3 3 а б c , V ограниченный знак равно 8 а б c . <\ displaystyle V _ <\ text
Площадь поверхности
Площадь поверхности общего (трехосного) эллипсоида равна
S знак равно 2 π c 2 + 2 π а б грех ( φ ) ( E ( φ , k ) грех 2 ( φ ) + F ( φ , k ) потому что 2 ( φ ) ) , <\ displaystyle S = 2 \ pi c ^ <2>+ <\ frac <2 \ pi ab><\ sin (\ varphi)>> \ left (E (\ varphi, k) \, \ sin ^ <2>(\ varphi) + F (\ varphi, k) \, \ cos ^ <2>(\ varphi) \ right),>
потому что ( φ ) знак равно c а , k 2 знак равно а 2 ( б 2 — c 2 ) б 2 ( а 2 — c 2 ) , а ≥ б ≥ c , <\ displaystyle \ cos (\ varphi) = <\ frac
и где F ( φ , k ) и E ( φ , k ) — неполные эллиптические интегралы первого и второго рода соответственно.
Площадь поверхности эллипсоида вращения (или сфероида) может быть выражена через элементарные функции :
S сплюснутый знак равно 2 π а 2 ( 1 + c 2 е а 2 Artanh е ) , куда е 2 знак равно 1 — c 2 а 2 а также ( c а ) , <\ displaystyle S _ <\ text <сжатый>> = 2 \ pi a ^ <2>\ left (1 + <\ frac
S сплюснутый знак равно 2 π а 2 ( 1 + 1 — е 2 е Artanh е ) <\ displaystyle S _ <\ text <сжатый>> = 2 \ pi a ^ <2>\ left (1 + <\ frac <1-e ^ <2>>
S сплюснутый знак равно 2 π а 2 + π c 2 е пер 1 + е 1 — е <\ Displaystyle S _ <\ текст <сплющенный>> = 2 \ pi a ^ <2>\ + <\ frac <\ pi c ^ <2>>
a),>»> S вытянутый знак равно 2 π а 2 ( 1 + c а е Arcsin е ) куда е 2 знак равно 1 — а 2 c 2 а также ( c > а ) , <\ displaystyle S _ <\ text 
которые, как следует из основных тригонометрических тождеств, являются эквивалентными выражениями (т. е. формулу для S сжатого можно использовать для вычисления площади поверхности вытянутого эллипсоида и наоборот). В обоих случаях е можно снова определить как эксцентриситет эллипса, образованного поперечным сечением оси симметрии. (См. Эллипс ). Вывод этих результатов можно найти в стандартных источниках, например Mathworld .
Примерная формула
S ≈ 4 π а п б п + а п c п + б п c п 3 п . <\ Displaystyle S \ приблизительно 4 \ pi <\ sqrt [
] <\ frac b ^
+ a ^
c ^
+ b ^
c ^
> <3>>>. \, \!>
Здесь p ≈ 1,6075 дает относительную ошибку не более 1,061%; значение p = 8 / 5 = 1,6 оптимально для эллипсоидов, близких к сферической, с относительной погрешностью не более 1,178%.
В «плоском» пределе c, намного меньшем, чем a и b , площадь составляет примерно 2π ab , что эквивалентно p ≈ 1,5850 .
Плоские секции
Характеристики
Пересечение плоскости и сферы представляет собой окружность (либо сводится к одной точке, либо пусто). Любой эллипсоид является изображением единичной сферы при некотором аффинном преобразовании, а любая плоскость является изображением некоторой другой плоскости при таком же преобразовании. Итак, поскольку аффинные преобразования преобразуют круги в эллипсы, пересечение плоскости с эллипсоидом является эллипсом, единственной точкой или пусто. Очевидно, что сфероиды содержат круги. Это также верно, но менее очевидно, для трехосных эллипсоидов (см. Круглый раздел ).
Определение эллипса плоского сечения
Дано: Эллипсоид х 2 / а 2 + y 2 / б 2 + z 2 / с 2 = 1 и плоскость с уравнением n x x + n y y + n z z = d , которые имеют общий эллипс.
Требуется: три вектора f 0 (центр) и f 1 , f 2 (сопряженные векторы), такие, что эллипс можно представить параметрическим уравнением
Икс знак равно ж 0 + ж 1 потому что т + ж 2 грех т <\ displaystyle \ mathbf
Решение: масштабирование u = Икс / а , v = у / б , w = z / c переводит эллипсоид на единичную сферу u 2 + v 2 + w 2 = 1 и заданную плоскость на плоскость с уравнением
п Икс а ты + п у б v + п z c ш знак равно d . <\ displaystyle \ n_
м знак равно [ м ты м v м ш ] <\ displaystyle \; \ mathbf
его единичный вектор нормали. Следовательно
е 0 знак равно δ м <\ displaystyle \ mathbf
является центром пересечений окружности и
ρ знак равно 1 — δ 2 <\ Displaystyle \; \ rho = <\ sqrt <1- \ delta ^ <2>>> \;>
его радиус (см. диаграмму).
Если m w = ± 1 (т. Е. Плоскость горизонтальна), пусть
е 1 знак равно [ ρ 0 0 ] , е 2 знак равно [ 0 ρ 0 ] . <\ displaystyle \ \ mathbf
е 1 знак равно ρ м ты 2 + м v 2 [ м v — м ты 0 ] , е 2 знак равно м × е 1 . <\ displaystyle \ mathbf
В любом случае векторы e 1 , e 2 ортогональны, параллельны плоскости пересечения и имеют длину ρ (радиус окружности). Следовательно, окружность пересечения может быть описана параметрическим уравнением
ты знак равно е 0 + е 1 потому что т + е 2 грех т . <\ displaystyle \; \ mathbf = \ mathbf
Обратное масштабирование (см. Выше) преобразует единичную сферу обратно в эллипсоид, а векторы e 0 , e 1 , e 2 отображаются на векторы f 0 , f 1 , f 2 , которые требовались для параметрического представления эллипса пересечения. .
Как найти вершины и полуоси эллипса, описано в эллипсе .
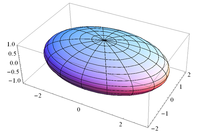
Пример: на диаграммах показан эллипсоид с полуосями a = 4, b = 5, c = 3, разрезанный плоскостью x + y + z = 5 .
Штифтовая конструкция
Конструкция эллипсоида в виде булавок и струн — это передача идеи построения эллипса с использованием двух булавок и веревки (см. Диаграмму).
Построение «кегли и струны» эллипсоида вращения дается конструкцией вращающегося эллипса «кегли».
Построение точек трехосного эллипсоида сложнее. Первые идеи принадлежат шотландскому физику Дж. К. Максвеллу (1868 г.). Основные исследования и распространение на квадрики были выполнены немецким математиком О. Штауде в 1882, 1886 и 1898 годах. Описание конструкции эллипсоидов и гиперболоидов с помощью булавок и струн содержится в книге « Геометрия и воображение», написанной Д. Гильберт и С. Фоссен тоже.
Этапы строительства
- Выберите эллипс E и гиперболу H , которые представляют собой пару фокальных коник : E ( φ ) знак равно ( а потому что φ , б грех φ , 0 ) ЧАС ( ψ ) знак равно ( c шиш ψ , 0 , б грех ψ ) , c 2 знак равно а 2 — б 2 <\ Displaystyle <\ begin <выровнено>E (\ varphi) & = (a \ cos \ varphi, b \ sin \ varphi, 0) \\ H (\ psi) & = (c \ cosh \ psi, 0, b \ sinh \ psi), \ quad c ^ <2>= a ^ <2>-b ^ <2>\ end
>>
с вершинами и фокусами эллипса
S 1 знак равно ( а , 0 , 0 ) , F 1 знак равно ( c , 0 , 0 ) , F 2 знак равно ( — c , 0 , 0 ) , S 2 знак равно ( — а , 0 , 0 ) <\ Displaystyle S_ <1>= (a, 0,0), \ quad F_ <1>= (c, 0,0), \ quad F_ <2>= (- c, 0,0), \ quad S_ <2>= (- а, 0,0)>

Полуоси
Уравнения для полуосей сгенерированного эллипсоида могут быть получены путем специального выбора для точки P :
Y знак равно ( 0 , р у , 0 ) , Z знак равно ( 0 , 0 , р z ) . <\ displaystyle Y = (0, r_
Нижняя часть диаграммы показывает, что F 1 и F 2 также являются фокусами эллипса в плоскости xy . Следовательно, она конфокальна данному эллипсу, а длина струны l = 2 r x + ( a — c ) . Решение относительно r x дает r x = 1 / 2 ( л — а + в ) ; кроме того, г 2
лет = г 2
х — с 2 .
Из верхней диаграммы мы видим, что S 1 и S 2 являются фокусами эллиптического сечения эллипсоида в плоскости xz и что r 2
z = г 2
х — а 2 .
Converse
Если, наоборот, трехосный эллипсоид задается его уравнением, то из уравнений на шаге 3 можно вывести параметры a , b , l для конструкции из булавок и струн.
Конфокальные эллипсоиды
Если Е представляет собой эллипсоид конфокальный к Е с квадратами его полуосей
р ¯ Икс 2 знак равно р Икс 2 — λ , р ¯ у 2 знак равно р у 2 — λ , р ¯ z 2 знак равно р z 2 — λ <\ displaystyle <\ overline
то из уравнений E
р Икс 2 — р у 2 знак равно c 2 , р Икс 2 — р z 2 знак равно а 2 , р у 2 — р z 2 знак равно а 2 — c 2 знак равно б 2 <\ displaystyle r_
можно обнаружить, что соответствующие координационные коники , используемые для штырей-и-струнной конструкции имеют одинаковые полуоси а , б , гр как эллипсоид Е . Поэтому (аналогично фокусам эллипса) фокальные коники трехосного эллипсоида рассматриваются как (бесконечное множество) фокусов и называются фокальными кривыми эллипсоида.
Верно и обратное утверждение: если выбрать вторую строку длины l и определить
λ знак равно р Икс 2 — р ¯ Икс 2 <\ displaystyle \ lambda = r_
р ¯ у 2 знак равно р у 2 — λ , р ¯ z 2 знак равно р z 2 — λ <\ displaystyle <\ overline
действительны, что означает, что два эллипсоида конфокальны.
Предельный случай, эллипсоид вращения
В случае a = c ( сфероид ) получаем S 1 = F 1 и S 2 = F 2 , что означает, что фокальный эллипс вырождается в отрезок прямой, а фокальная гипербола схлопывается до двух бесконечных отрезков прямой на оси x. . Эллипсоид вращательно-симметричен относительно оси x и
р Икс знак равно л 2 , р у знак равно р z знак равно р Икс 2 — c 2 <\ displaystyle r_ 
Свойства фокальной гиперболы
Свойство фокального эллипса
Фокальный эллипс вместе с его внутренней частью можно рассматривать как предельную поверхность (бесконечно тонкий эллипсоид) пучка софокусных эллипсоидов, определяемого параметрами a , b при r z → 0 . Для предельного случая получаем
р Икс знак равно а , р у знак равно б , л знак равно 3 а — c . <\ displaystyle r_
В общем положении
Как квадрика
Если v — точка, а A — вещественная симметричная положительно определенная матрица , то набор точек x , удовлетворяющих уравнению
( Икс — v ) Т А ( Икс — v ) знак равно 1 <\ displaystyle (\ mathbf
эллипсоид с центром в v . В собственных векторах из А являются главными осями эллипсоида, а собственные значения из A являются обратными квадратами полуосей: -2 , б -2 и с -2 .
Обратимое линейное преобразование, примененное к сфере, дает эллипсоид, который может быть приведен к указанной выше стандартной форме подходящим вращением , что является следствием полярного разложения (также см. Спектральную теорему ). Если линейное преобразование представлено симметричной матрицей 3 × 3 , то собственные векторы матрицы ортогональны (согласно спектральной теореме ) и представляют направления осей эллипсоида; длины полуосей вычисляются из собственных значений. Сингулярное разложение и полярное разложение матричные разложения тесно связаны с этими геометрическими наблюдениями.
Параметрическое представление
Ключом к параметрическому представлению эллипсоида в общем положении является альтернативное определение:
Эллипсоид — это аффинное изображение единичной сферы.
Аффинное преобразование может быть представлено в виде перевода с вектором ф 0 и регулярным 3 × 3 матрицы A :
Икс ↦ ж 0 + А Икс знак равно ж 0 + Икс ж 1 + у ж 2 + z ж 3 <\ displaystyle \ mathbf
Параметрическое представление эллипсоида общего положения может быть получено с помощью параметрического представления единичной сферы (см. Выше) и аффинного преобразования:
Икс ( θ , φ ) знак равно ж 0 + ж 1 потому что θ потому что φ + ж 2 потому что θ грех φ + ж 3 грех θ , — π 2 θ π 2 , 0 ≤ φ 2 π <\ displaystyle \ mathbf 
Если векторы f 1 , f 2 , f 3 образуют ортогональную систему, шесть точек с векторами f 0 ± f 1,2,3 являются вершинами эллипсоида и | f 1 |, | f 2 |, | f 3 | — полуглавные оси.
Вектор нормали к поверхности в точке x ( θ , φ ) равен
п ( θ , φ ) знак равно ж 2 × ж 3 потому что θ потому что φ + ж 3 × ж 1 потому что θ грех φ + ж 1 × ж 2 грех θ . <\ displaystyle \ mathbf
Для любого эллипсоида существует неявное представление F ( x , y , z ) = 0 . Если для простоты центр эллипсоида является началом координат, f 0 = 0 , следующее уравнение описывает эллипсоид выше:
F ( Икс , у , z ) знак равно Det ( Икс , ж 2 , ж 3 ) 2 + Det ( ж 1 , Икс , ж 3 ) 2 + Det ( ж 1 , ж 2 , Икс ) 2 — Det ( ж 1 , ж 2 , ж 3 ) 2 знак равно 0 <\ Displaystyle F (x, y, z) = \ operatorname
Приложения
Эллипсоидальная форма находит множество практических применений:
Геодезия
- Эллипсоид Земли , математическая фигура, приближающая форму Земли .
- Справочный эллипсоид , математическая фигура, аппроксимирующая форму планетных тел в целом.
Механика
- Эллипсоид Пуансо , геометрический метод для визуализации движения без крутящего момента вращающегося твердого тела .
- Эллипсоид напряжений Ламе , альтернатива кругу Мора для графического представления напряженного состояния в точке.
- Эллипсоид управляемости , используемый для описания свободы движения робота.
- Эллипсоид Якоби , трехосный эллипсоид, образованный вращающейся жидкостью.
Кристаллография
- Индексный эллипсоид , диаграмма эллипсоида, изображающая ориентацию и относительную величину показателей преломления в кристалле .
- Тепловой эллипсоид , эллипсоиды, используемые в кристаллографии для обозначения величин и направлений тепловых колебаний атомов в кристаллических структурах .
Осветительные приборы
- Эллипсоидальный прожектор с отражателем
- Прожектор с эллипсоидальным рефлектором
Медицина
- Измерения , полученные из МРТ визуализации простаты могут быть использованы для определения объема железы с помощью аппроксимации L × Ш × Н × 0,52 (где 0,52 приблизительный π / 6 )
Динамические свойства
Масса эллипсоида равномерной плотности р является
м знак равно V ρ знак равно 4 3 π а б c ρ . <\ displaystyle m = V \ rho = <\ tfrac <4><3>> \ pi abc \ rho.>
В моменты инерции эллипсоида однородной плотности являются
я Икс Икс знак равно 1 5 м ( б 2 + c 2 ) , я у у знак равно 1 5 м ( c 2 + а 2 ) , я z z знак равно 1 5 м ( а 2 + б 2 ) , я Икс у знак равно я у z знак равно я z Икс знак равно 0. <\ displaystyle <\ begin
При a = b = c эти моменты инерции сводятся к моментам инерции для сферы однородной плотности.
Эллипсоиды и кубоиды стабильно вращаются вдоль своей большой или малой оси, но не вдоль средней оси. Это можно увидеть экспериментально, бросив ластик с некоторым вращением. Кроме того, соображения момента инерции означают, что вращение вдоль большой оси более легко нарушить, чем вращение вдоль малой оси.
Одним из практических последствий этого является то, что разносторонние астрономические тела, такие как Хаумеа, обычно вращаются вдоль своих малых осей (как и Земля, которая просто сплюснута ); кроме того, из-за приливной блокировки спутники находятся на синхронной орбите, такие как орбита Мимаса, с их большой осью, выровненной радиально по отношению к их планете.
Вращающееся тело из однородной самогравитирующей жидкости примет форму сфероида Маклорена (сплюснутый сфероид) или эллипсоида Якоби (разносторонний эллипсоид), когда оно находится в гидростатическом равновесии и при умеренных скоростях вращения. При более быстром вращении можно ожидать неэллипсоидальных грушевидных или яйцевидных форм, но они нестабильны.
Динамика жидкостей
Эллипсоид — это наиболее общая форма, для которой можно было рассчитать ползущий поток жидкости вокруг твердого тела. В расчетах учитывается сила, необходимая для перемещения в жидкости и вращения в ней. Приложения включают определение размера и формы больших молекул, скорости опускания мелких частиц и способности микроорганизмов плавать .
По вероятности и статистике
В эллиптических распределениях , обобщающие многомерное нормальное распределение и используются в области финансов , могут быть определены в терминах их функций плотности . Когда они существуют, функции плотности f имеют структуру:
ж ( Икс ) знак равно k ⋅ грамм ( ( Икс — μ ) Σ — 1 ( Икс — μ ) Т ) <\ displaystyle f (x) = k \ cdot g \ left ((\ mathbf
где k — масштабный коэффициент, x — n- мерный случайный вектор-строка со средним вектором μ (который также является средним вектором, если последний существует), Σ — положительно определенная матрица, которая пропорциональна ковариационной матрице, если последняя существует , а g — отображение функции неотрицательных вещественных чисел в неотрицательные числа, дающее конечную площадь под кривой. Многомерное нормальное распределение — это частный случай, когда g ( z ) = exp (- z / 2 ) для квадратичной формы z .
Таким образом, функция плотности представляет собой скалярное преобразование квадратичного выражения в скалярное преобразование. Более того, уравнение для любой поверхности изоплотности утверждает, что выражение квадрики равно некоторой константе, специфичной для этого значения плотности, а поверхность изоплотности является эллипсоидом.
В высших измерениях
Hyperellipsoid или эллипсоид размерности в евклидовом пространстве размерности , является квадратичная гиперповерхность определяется полиномом второй степени , который имеет однородную часть второй степени , которая является положительно определенной квадратичной формой . п — 1 <\ displaystyle n-1> 
Можно также определить гиперэллипсоид как изображение сферы при обратимом аффинном преобразовании . Спектральная теорема снова может быть использована для получения стандартного уравнения вида
Икс 1 2 а 1 2 + Икс 2 2 а 2 2 + ⋯ + Икс п 2 а п 2 знак равно 1. <\ displaystyle <\ frac
Объем n- мерного гиперэллипсоида можно получить, заменив R n произведением полуосей a 1 a 2 . a n в формуле для объема гиперсферы :
V знак равно π п 2 Γ ( п 2 + 1 ) а 1 а 2 ⋯ а п <\ displaystyle V = <\ frac <\ pi ^ <\ frac
Источник