Что значит эквивалентные матрицы

Эквивалентные матрицы

Пусть R и S два векторных пространства размерности n и m соответственно над числовым полем K, и пусть A линейный оператор отображающий R в S . Выясним, как меняется матрица оператора A при изменении базисов в пространствах R в S.

Выберем произвольные базисы в пространствах R в S и обозначим через и соответственно. Тогда (см. в линейные операторы) векторному равенству

соответствует матричное равенство

где х и у векторы x и y, представленные в виде координатных столбцов в базисах и соответственно.

Выберем теперь в пространствах R и S другие базисы и. В новых базисах векторному равенству (1) будет соответствовать матричное равенство

Обозначим через Q и P невырожденные квадратные матрицы порядков n и m соответственно, которые осуществляют преобразование координат в пространствах R и S при переходе от старых базисов к новым (см. линейное пространство). Тогда связь между векторами в старых и новых базисах можно представить следующими равенствами:

x’=Qx, y’=Py.

(4)

Тогда, учитывая (3) и (4), имеем

y’=Py=PAx=PAQ -1 x’.

(5)

Обозначив T=Q −1 , и учитывая (3) и (5) получим:

Определение 1. Две прямоугольные матрицы A и B одинаковых размеров называются эквивалентными, если существуют две квадратные невырожденные матрицы P и T такие, что выполнено равенство

Отметим, что если A -матрица порядка m×n, то P и T квадратные матрицы порядков m и n, соответственно.

Из (6) следует, что две матрицы, соответствующие одному и тому же линейному оператору A при различном выборе базисов в пространствах R и S эквивалентны между собой. Верно и обратное утверждение. Если матрица A соответствует оператору A, а матрица B эквивалентна матрице A, то она соответствует этому же линейному оператору A при других базисах в R и S.

Выясним, при каких условиях две матрицы эквивалентны.

Теорема. Для того, чтобы две матрицы одинаковых размеров были эквивалентны между собой, необходимо и достаточно, чтобы они имели один и тот же ранг.

Доказательство. Необходимость. Так как умножение матрицы на квадратную невырожденную матрицу не может изменить ранг матрицы, то из (7) имеем:

rang B=rang A.

Достаточность. Пусть задан линейный оператор A, отображающий пространство R в S и пусть этому оператору отвечает матрица A размера m×n в базисах в R и в S, соответственно. Обозначим через r число линейно независимых векторов из числа Ae₁, Ae₂. Ae_n. Пусть линейно независимы первые r векторы Ae₁, Ae₂. Ae_r. Тогда остальные n-r векторы выражаются линейно через эти векторы:

Aek= n cij Aej, (k=r+1. n) ∑ j= 1

(8)

Зададим новый базис в пространстве R:

Тогда учитывая (8), имеем:

Далее выберем векторы в качестве векторов базиса в S:

fj‘= Aej‘, j=1,2. r

(10)

Дополним эти векторы некоторыми векторами до базиса в S.

Тогда матрица оператора A в новых базисах , согласно (9) и (10) будет иметь следующий вид:

(11)

где в матрице E ‘ -на главной диагонали стоят r единиц, а остальные элементы равны нулю.

Так как матрицы A и E ‘ соответствуют одному и тому же оператору A, то они эквивалентны между собой. Выше мы показали, что эквивалентные матрицы имеют один и тот же ранг, следовательно ранг исходной матрицы A равен r.

Из вышеуказанного следует, что произвольная m×n матрица ранга r эквивалентна матрице E ‘ — порядка m×n. Но E ‘ — однозначно определяется заданием размерности m×n матрицы и его ранга r. Следовательно все прямоугольные матрицы порядка m×n и ранга r эквивалентны одной и той же матрице E ‘ и, следовательно, эквивалентны между собой.■

Источник

Равенство матриц, эквивалентные матрицы

Вы будете перенаправлены на Автор24

В теории матриц часто встречаются понятия равенства и эквивалентности матриц.

Матрица $A=\left(a_ \right)_ $ называется равной матрице $B=\left(b_ \right)_ $, если их размерности совпадают $(m=k,n=l)$ и соответствующие элементы сравниваемых матриц равны между собой.

Для матриц 2-го порядка, записанных в общем виде, равенство матриц можно записать следующим образом:

Определить, равны ли матрицы.

Матрицы А и В имеют одинаковый порядок, равный 2$\times $2. Соответствующие элементы сравниваемых матриц равны, следовательно, матрицы равны.

Матрицы А и В имеют разный порядок, равный 2$\times $2 и 2$\times $1 соответственно.

Матрицы А и В имеют одинаковый порядок, равный 2$\times $2. Однако не все соответствующие элементы сравниваемых матриц равны, следовательно, матрицы не являются равными.

Готовые работы на аналогичную тему

Элементарное преобразование матрицы — это такое преобразование, в результате которого сохраняется эквивалентность матриц. Другими словами, элементарное преобразование не изменяет множества решений системы линейных алгебраических уравнений (СЛАУ), которую представляет данная матрица.

К элементарным преобразованиям строк матриц относятся:

• умножение строки матрицы на число $k$, не равное нулю (определитель матрицы при этом увеличивается в $k$ раз);
• перестановка местами двух любых строк матрицы;
• прибавление к элементам одной строки матрицы элементов другой ее строки.

То же самое применимо и к столбцам матрицы и называется элементарными преобразованиями столбцов.

Если от матрицы А с помощью элементарного преобразования перешли к матрице В, то исходная и полученная матрицы называются эквивалентными. Для обозначения эквивалентности матриц используют знак «$ \sim$», например, $A\sim B$.

Выполнить по очереди элементарные преобразования строк матрицы.

Поменяем местами первую строку и вторую строку матрицы А:

Умножим первую строку матрицы В на число 2:

Сложим первую строку со второй строкой матрицы:

Ступенчатая матрица — это матрица, которая удовлетворяет следующим условиям:

• при наличии в матрице нулевой строки все строки, находящиеся ниже ее, тоже являются нулевыми;
• первый ненулевой элемент каждой ненулевой строки должен быть расположен строго правее ведущего элемента в строке, которая находится выше данной.

Привести матрицу к ступенчатому виду можно с помощью эквивалентных преобразований.

Дана матрица: $A=\left(\begin <-2>& <1>& <4>\\ <1>& <0>& <3>\\ <1>& <2>& <3>\end\right)$. Выполнить приведение матрицы к ступенчатому виду.

Поменяем местами первую и вторую строки матрицы А:

Умножим первую строку матрицы В на число 2 и сложим ее со второй строкой:

Умножим первую строку матрицы С на число -1 и сложим ее с третьей строкой:

Умножим вторую строку матрицы D на число -2 и сложим ее с третьей строкой:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 18 11 2021

Источник

Эквивалентные преобразования матрицы

В данной публикации мы рассмотрим, что такое элементарные (эквивалентные) преобразования матрицы, какие бывают виды, а также разберем примеры для демонстрации теории на практике.

Определение и виды элементарных преобразований

Элементарными называются такие преобразования матрицы, при которых сохраняется эквивалентность матриц (из-за этого их часто называют эквивалентными). Другими словами такие преобразования не меняют множество решений СЛАУ, которая представлена данной матрицей.

Элементарные преобразования применяются в метода Гаусса, чтобы привести матрицу к треугольному или ступенчатому виду.

К элементарным преобразованиям относятся:

• перестановка двух любых строк местами;
• умножение любой строки на ненулевую константу;
• сумма двух любых строк, одна из которых умножена на определенное ненулевое число.

Примечание: аналогичные действия применимы и к столбцам матрицы.

Матрицы A и B являются эквивалентными, если B получена путем элементарных преобразований A (или наоборот). Для обозначения эквивалентности используется специальный символ – “

Примеры эквивалентных преобразований матрицы

Давайте на примере матрицы ниже покажем все виды элементарных преобразований.

1. Поменяем вторую и третью строки местами.

2. Умножим первую строку на число 3.

3. Вычтем из третьей строки удвоенную вторую.

Источник

Элементарные преобразования над строками матрицы.Эквивалентные матрицы

Элементарными преобразованиями над строками матриц называются следующие преобразования строк:

1. умножение строки на ненулевое число;
2. перестановка двух строк;
3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число.

Если от матрицы $A$ к матрице $B$ перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают $A \sim B$ .

Примеры элементарных преобразований

Продемонстрируем все элементарные преобразования на примере матрицы $A=\left(\begin 1 & 3 & 3 \\ 3 & 2 & 2 \end\right)$

Умножим первую строку матрицы на два, то есть каждый элемент первой строки умножаем на двойку, в результате получим матрицу $B$ , эквивалентную заданной матрице $A$ :

$$A=\left(\begin 1 & 3 & 3 \\ 3 & 2 & 2 \end\right) \sim B=\left(\begin 1 \cdot 2 & 3 \cdot 2 & 3 \cdot 2 \\ 3 & 2 & 2 \end\right)=\left(\begin 2 & 6 & 6 \\ 3 & 2 & 2 \end\right)$$

Поменяем первую и вторую строки матрицы $B$ местами, получаем эквивалентную ей матрицу $C$ :

$$B=\left(\begin 2 & 6 & 6 \\ 3 & 2 & 2 \end\right) \sim C=\left(\begin 3 & 2 & 2 \\ 2 & 6 & 6 \end\right)$$

От первой строки матрицы $C$ отнимем вторую строку, получаем эквивалентную матрицу $D$ :

$$C=\left(\begin 3 & 2 & 2 \\ 2 & 6 & 6 \end\right) \sim D=\left(\begin 3-2 & 2-6 & 2-6 \\ 2 & 6 & 6 \end\right)=\left(\begin 1 & -4 & -4 \\ 2 & 6 & 6 \end\right)$$

В итоге делаем вывод, что матрицы $A$ и $D$ эквивалентны, так как от одной из них перешли к другой при помощи эквивалентных преобразований над строками.

Источник

Эквивалентность матриц

Простейший вид матрицы линейного оператора.

Матрицы A и B называются эквивалентными, если найдутся невырожденные матрицы Q и T, что A=QBT.

Теорема 6.1. Если матрицы эквивалентны, то их ранги равны.

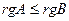
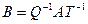
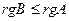
Доказательство. Поскольку ранг произведения не превосходит ранги сомножителей, то . Так как , то . Объединяя два неравенства, получаем требуемое утверждение.

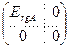
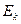
Теорема 6.2. Элементарными преобразованиями со строками и столбцами матрицу A можно привести к блочному виду , где — единичная матрица порядка k, а 0 – нулевая матрица соответствующих размеров.

Доказательство. Приведем алгоритм приведения матрицы A к указанному виду. Номера столбцов будут указываться в квадратных скобках, а номера строк – в круглых скобках.

2. Если 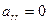то перейдем на шаг 4, иначе перейдем на шаг 3.

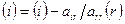
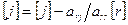
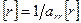
3. Сделаем преобразования со строками , где i=r+1,…,m, и со столбцами , где j=r+1,…,n, и . Увеличим r на 1 и вернемся на шаг 2.

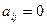
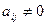
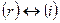
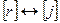
4. Если , при i=r+1,…,m, j=r+1,…,n, то конец. В противном случае найдем i,j>r, что . Переставим строки и столбцы , вернемся на шаг 2.

Очевидно, что алгоритмом будет строиться последовательность эквивалентных матриц, последняя из которых имеет требуемый вид.

Теорема 6.3. Матрицы A и B одинаковых размеров эквивалентны тогда и только тогда, когда их ранги равны.

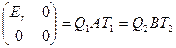
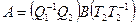
Доказательство. Если матрицы эквивалентны, то их ранги равны (Теорема 6.1). Пусть ранги матриц равны. Тогда найдутся невырожденные матрицы, что , где r=rgA=rgB (Теорема 6.2). Следовательно, , и матрицы A и B – эквивалентны.

Результаты данного пункта позволяют находить простейший вид матрицы линейного оператора и базисы пространств, в которых матрица линейного оператора имеет этот простейший вид.

Источник

Читайте также:  У меня было шесть пальцев что это значит