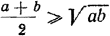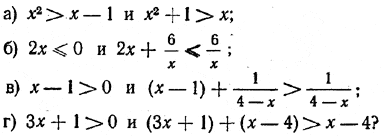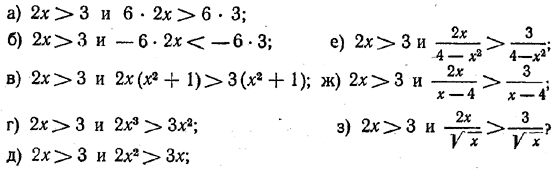Что значит эквивалентно неравенству
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I
§ 20 Эквивалентные неравенства и их свойства
До сих пор мы рассматривали тождественные неравенства, то есть такие неравенства, которые выполняются (обращаются в числовые неравенства) при всех допустимых или специально указанных значениях входящих в них букв. К таким относятся, например, неравенства:
а + 1 > а, а 2 > 0, 
Теперь мы переходим к изучению неравенств, которые выполняются не при всех, а лишь при некоторых (а может быть, и ни. при каких!) допустимых значениях букв. Примером такого неравенства может служить неравенство
Оно выполняется при любых положительных значениях х, хотя допустимыми значениями х являются все числа, в том числе и отрицательные.
Решить неравенство, содержащее неизвестную величину, — это значит найти все те значения этой неизвестной величины, при которых данное неравенство выполняется.
Подобно решению уравнений, решение неравенств обычно проводится путем сведения их к более простым, эквивалентным (или равносильным) неравенствам.
Два неравенства, содержащие одну и ту же неизвестную величину, называются эквивалентными (или равносильными), если они выполняются при одних и тех же значениях этой величины.
Примером эквивалентных неравенств могут служить неравенства 2х > 0 и —3х 0 и х 2 > 0 не эквивалентны, поскольку первое из них верно только при положительных значениях х, а второе — как при положительных, так и при отрицательных значениях х.
Неравенства, каждое из которых не выполняется ни при каких значениях неизвестной величины, также считаются эквивалентными. Примером таких неравенств могут служить неравенства
Эквивалентные неравенства обладают рядом важных свойств, которые мы приводим без доказательства.
Свойство 1. Если к обеим частям неравенства прибавить или из обеих частей вычесть число или выражение, определенное для всех значений неизвестной величины, то получится неравенство, эквивалентное данному.
Примеры. 1) Если к обеим частям неравенства х > 2 — х прибавить число —2, то в результате получится неравенство х — 2 > —х. Это неравенство, как утверждает свойство 1, должно быть эквивалентно данному неравенству х > 2 — х.
2) Прибавим к каждой части неравенства 1 /x 1 /x 0 выражение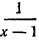 
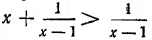
, мы получим неравенство 
. Исходное неравенство верно при всех положительных значениях х и, в частности, при х = 1. Полученное же неравенство при х = 1 не имеет смысла. Поэтому при х = 1 оно выполняться не может. Таким образом, рассматриваемые два неравенства не эквивалентны.
Из первого свойства эквивалентных неравенств вытекает важное для дальнейшего следствие. Любое слагаемое, определенное для всех значений неизвестной величины, можно перенести из одной части неравенства в другую, поменяв знак этого слагаемого на противоположный.
Действительно, пусть дано неравенство
где Р(х), Q(х) и R(х) представляют собой некоторые выражения, зависящие от х, причем Q(х) определено для любых значений х. Нам нужно доказать, что такое неравенство эквивалентно неравенству
Доказательство этого факта очень простое: неравенство (2) получается, если из обеих частей неравенства (1) отнять Q(х).
Пример. Пусть дано неравенство 3х + 1 1 /4. При этих же значениях х должно, следовательно, выполняться и данное неравенство 3х + 1 0,
которое не эквивалентно исходному неравенству.
Свойство 2. Если обе части неравенства умножить на положительное число или выражение, принимающее только положительные значения и определенное для всех значений неизвестной величины, то получится неравенство, эквивалентное данному.
Примеры. 1) Если обе части неравенства х > 2 — х умножить на положительное число 3, то получится неравенство 3х > 6 — 3х, эквивалентное данному.
2) Выражение х 2 + 1 принимает только положительные значения и определено для всех значений х. Поэтому неравенство х 2 + 1) 2 + 1,
Следует особо подчеркнуть, что то выражение, на которое мы умножаем обе части исходного неравенства, должно удовлетворять двум требованиям:
а) оно обязано принимать только положительные значения и
б) быть определенным для всех значений неизвестной величины.
Если хотя бы одно из этих требований не удовлетворяется, то исходное и полученное из него неравенства могут оказаться неэквивалентными. Поясним это на следующих примерах.
1) Неравенство х > 0 выполняется только для положительных значений х. Умножив его почленно на х, мы получим неравенство х 2 > 0. Оно верно как для положительных, так и для отрицательных значений х. Несоответствие этого результата со свойством 2 легко объяснить. Ведь выражение х, на которое мы умножили обе части исходного неравенства х > 0, принимает как положительные, так и отрицательные значения. А на этот случай свойство 2 не дает никаких гарантий.
2) Умножив неравенство х > 0 на выражение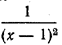 
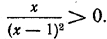
, мы получим неравенство 
Предлагаем учащимся самостоятельно показать, что это неравенство не эквивалентно данному, и объяснить, почему 2-е свойство эквивалентных неравенств здесь не применимо.
Свойство 3. Если обе части неравенства умножить на отрицательное число или выражение, которое определено для всех значений неизвестной величины и принимает только отрицательные значения, а знак неравенства изменить на противоположный ( > на ), то получится неравенство, эквивалентное данному.
Это свойство вполне аналогично 2-му свойству. Поэтому подробно останавливаться на нем мы не будем.
152. Эквивалентны ли неравенства:
153. Эквивалентны ли неравенства:
152. а) Да; б) нет; в) нет; г) да. 153. а) Да; б) да; в) да; г) да; д) нет; е) нет; ж) нет; з). да.
Источник
Что значит эквивалентно неравенству
6.4 эквивалентные неравенства
Определение. Два неравенства f1(x) > g1(x) и
y
называются равносильными или эквивалентными, если множества их решений совпадают
Другими словами, два неравенства являются эквивалентными, если решения первого неравенства являются решениями второго неравенства, а решения второго неравенства являются решениями
первого неравенства. Если два неравенства эквивалентны, то между ними ставится знак ⇔.
2 x 10 ⇔ x − 2 3, потому что каждое неравенство имеет множество решений ]5;
+∞[. Два неравенства с одинаковой переменной, которые не имеют решений, также равносильны, по
тому что их множество решений ∅.
Теорема 1. Если к левой и правой части неравенства f(x)
> g(x) прибавить одно и то же число или выражение F(x), которое имеет смысл при всех допустимых значениях переменной данного неравенства, то получим неравенство эквивалентное данному неравенству
Доказательство. Сначала покажем, что все решения данного неравенства f(x) > g(x) являются решениями неравенства f(x) + + F(x) > g(x) + F(x). Пусть число a – любое решение данного неравенства. Тогда верно неравенство f(a) > g(a). Прибавим к обеим частям этого неравенства число F(a). Мы получим верное числовое неравенство f(x) + F(x) > g(x) + F(x). Отсюда следует, что число a является решением неравенства f(x) + F(x) > g(x) + F(x). Но a – это произвольно выбранное число из множества решений данного неравенства. Поэтому мы доказали, что все решения данного неравенства являются решениями нового неравенства.
Следствие. Члены неравенства можно переносить из одной части неравенства в другую часть с противоположным знаком.
Теорема 2. Если обе части неравенства f(x) > g(x) умножить или разделить на одно и то же положительное число m,
то получатся неравенства того же смысла
m m
Эти неравенства эквивалентны данному неравенству f(x)
Теорема 3. Если обе части неравенства f(x) > g(x) умножить или разделить на одно и то же отрицательное число m, то получатся неравенства противоположного смысла
m m
Эти неравенства эквивалентны данному неравенству f(x) >
Содержание
Читать: Аннотация
Читать: Введение
Читать: 1 алгебраические выражения. одночлены и многочлены
Читать: 1.1 выражение. числовое значение выражения. одночлены и многочлены Читать: 1.2 целые алгебраические выражения.Читать: 1.3 деление целых алгебраических выраженийЧитать: 1.4 формулы сокращенного умноженияЧитать: 1.5 разложение многочленов на множители
Читать: 2 алгебраические дробиЧитать: 2.1 определение. основное свойство алгебраической дробиЧитать: 2.2 выделение целой части из алгебраической дроби
Читать: 3 уравнения. линейные уравненияЧитать: 3.1 равенства и их свойстваЧитать: 3.2 равносильные (эквивалентные) уравненияЧитать: 3.3 свойства равносильности уравнений.Читать: 3.4 область допустимых значений уравненияЧитать: 3.5 решение линейного уравнения с одним неизвестнымЧитать: 3.6 линейное уравнение с двумя неизвестными
Читать: 4 системы линейных уравненийЧитать: 4.1 система двух линейных уравнений с двумя неизвестнымиЧитать: 4.2 равносильные (эквивалентные) системыЧитать: 4.3 методы решения системы двух линейных уравнений с двумя неизвестнымиЧитать: 4.4 решение системы уравнений методом определителейЧитать: 4.5 система трех линейных уравнений с тремя неизвестными
Читать: 5 квадратные уравненияЧитать: 5.1 определение квадратного уравненияЧитать: 5.2 решение неполных квадратных уравненийЧитать: 5.3 решение полного квадратного уравненияЧитать: 5.4 свойства корней квадратного уравненияЧитать: 5.5 разложение квадратного трехчлена на множителиЧитать: 5.6 биквадратные уравнения.
Читать: 6 неравенстваЧитать: 6.1 основные понятия и определенияЧитать: 6.2 свойства числовых неравенствЧитать: 6.3 неравенства с одной переменнойЧитать: 6.4 эквивалентные неравенстваЧитать: 6.5 линейные неравенства и их решениеЧитать: 6.6 система линейных неравенств
Читать: 7 решение нелинейных уравнений и системЧитать: 7.1 уравнения, которые содержат модульЧитать: 7.2 рациональные уравненияЧитать: 7.3 иррациональные уравненияЧитать: 7.4 системы алгебраических уравненийЧитать: 7.5 показательные уравнения и системы
Читать: Список литературы
Источник
