Что значит экспоненциально убывает

Что такое Экспонента

В этой статье нет ни слова о коронавирусе!

Экспоненциальный рост — одно из частых выражений в интернете, что же такое экспонента, давайте разложим «по полкам» и на примерах.

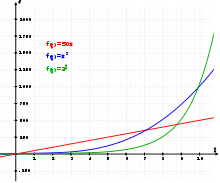
В математике экспонента «в чистом виде» — это показательная функция y(x) = ex, производная которой равна самой функции. Коэффициент e = 2,72 (число Эйлера). Рост такой функции происходит очень быстро, чем больше x, тем быстрее рост. К примеру, для х=0 экспонента равна 1, при х=1 функция растет до 2,72, а уже на х=5 она принимает значение 148. На графиках это выглядит как кривая, стремительно поднимающаяся вверх.

Представьте себе снежный ком который катится с горы, он постоянно увеличивается. Чем больше он становится, тем быстрее катится, чем быстрее катится, тем быстрее растет, получается расстояние, которое проходит снежный ком, зависит от времени как экспонента и его скорость выражается той же самой экспонентой.

У экспоненциально протекающих процессов есть одно общее свойство: за одинаковый интервал времени их параметры меняются в одинаковое число раз. Банковский вклад каждый год увеличивается на 7%, снежный ком за минуту увеличивается в три раза, а количество урана-235 на атомных электростанциях уменьшается вдвое каждые 700 миллионов лет. Экспоненциальные функции окружают нас повсюду. Экспоненциально развиваются все явления, в которых присутствует обратная связь, когда результат влияет на скорость процесса. В случае со снежным комом обратная связь положительная: чем больше результат, тем быстрее протекает процесс. А масса и скорость снежного кома y экспоненциально возрастают со временем x . Аналогично ведут себя деньги в банке при фиксированной процентной ставке. Чем больше денег, тем больше ежегодный прирост — и тем быстрее денег хватит на домик на Мальдивах. Так же увеличивается численность животных при отсутствии внешних угроз: чем больше популяция, тем больше размножающихся особей, тем быстрее она увеличивается. А еще, когда микрофон подносишь близко к динамику, то самый тихий шорох через секунду превратится в звонкий гул.

(При подготовке статьи были использованы материалы кандидата физико-математических наук, старшего научного сотрудника физического факультета МГУ Константина Катамадзе).

Пишите в комментариях о каких новых словах или терминах вы хотели бы узнать.

Источник

Экспоненциальный рост

Экспоненциальный рост — возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону. Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейному, степенному или геометрическому зависимостям.

Содержание

Свойства

Для любой экспоненциально растущей величины, чем большее значение она принимает, тем быстрее растет. Также это означает, что величина зависимой переменной и скорость ее роста прямо пропорциональны. Но при этом, в отличие от гиперболической экспоненциальная кривая никогда не уходит в бесконечность за конечный промежуток времени.

Экспоненциальный рост в итоге оказывается более быстрым, чем любая геометрическая прогрессия, чем любой степенной, и тем более, чем любой линейный рост.

Математическая запись

Экспоненциальный рост описывается дифференциальным уравнением:

Решение этого дифференциального уравнения — экспонента:

Примеры

Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов. Другим примером экспоненциального роста являются сложные проценты.

См. также

Ссылки

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Экспоненциальный рост» в других словарях:

ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ — Возрастание величины (возрастание в геометрической прогрессии), которая растет со скоростью, пропорциональной ее значению. Говорят: такой рост подчиняется экспоненциальному закону . Это означает, что для любой экспоненциально растущей величины,… … Словарь бизнес-терминов

экспоненциальный рост — eksponentinis didėjimas statusas T sritis fizika atitikmenys: angl. exponential rising vok. Exponentialanstieg, m rus. экспоненциальный рост, m pranc. accroissement exponentiel, m … Fizikos terminų žodynas

ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ — рост с относительно постоянной скоростью … Словарь ботанических терминов

Рост — процесс увеличения какого либо качества со временем. Качества могут быть как физическими (например, рост в высоту), так и абстрактными (например, взросление человека, расширение системы): Клеточный рост, или пролиферация Рост населения Рост… … Википедия

РОСТ — означает увеличение размеров развивающегося организма. В типичных случаях Р. связан с увеличением массы, однако не всякое увеличение массы организма мы , обозначаем как Р. (напр. отложение жира, накопление половых продуктов у некоторых животных,… … Большая медицинская энциклопедия

Закон экспоненциального роста — Экспоненциальный рост в математике экспоненциальное возрастание величины (возрастание в геометрической прогрессии), которая растет со скоростью, пропорциональной её значению. Говорят что такой рост подчиняется экспоненциальному закону. Это… … Википедия

АЛГОРИТМ — [от algorithm!; algorismus, первоначально лат. транслитерация имени ср. азиат. учёного 9 в. Хорезми (Мухаммед бен Муса аль Хорезми)], программа, определяющая способ поведения (вычисления); система правил (предписаний) для эффективного… … Философская энциклопедия

КОЛЕБАНИЯ — движения или процессы, обладающие той или иной степенью повторяемости во времени. К. свойственны всем явлениям природы: пульсирует излучение звёзд, внутри к рых происходят циклич. яд. реакции; с высокой степенью периодичности вращаются планеты… … Физическая энциклопедия

ДИОФАНТОВЫХ УРАВНЕНИИ ПРОБЛЕМА РАЗРЕШИМОСТИ — проблема отыскания алгоритма для распознавания по любому диофантову уравнению, имеет ли оно решение. Существенным в постановке проблемы является требование найти универсальный метод, к рый должен быть пригоден для любого уравнения (все известные… … Математическая энциклопедия

Перцептрон — Логическая схема перцептрона с тремя выходами Перцептрон, или персептрон[nb 1] (англ. perceptron от … Википедия

Источник

Экспоненциальный рост

Журналисты, блогеры и диванные эксперты… Все используют фразы «экспоненциальный рост», а кто по проще «рост по экспоненте». Кое-кто, наверное, даже помнит, что такое экспонента, но вряд ли сможет объяснить простыми словами. Что же, пришла пора разобраться то, чем мы так часто пользуемся. Возможно, все совсем не так…

Экспонента

Здесь все просто (но это только пока). Многие считают, что экспонента это просто число е=2,718281828459045235360287. Конечно, это не так. Это самое число e, называется числом Эйлера, оно трансцендентно и иррационально, что звучит красиво и загадочно, но экспонента, не число, а функция.

Те, кто немного дружил с математикой в школе сразу заметят интересную особенность этой функции. Ее основанием является не отрицательное число, а значит, она будет всегда возрастать.

При х=0 у=1, при х=1, у=2,718, при х=2 y=7,39…. Ну а при х=10, у=22 026,5

Значение функции растет и растет явно очень быстро. Стремительно и неудержимо.

Экспоненциальный рост

Что такое экспоненциальный рост? Простыми словами, это такой рост, при котором, чем больше вырастят какое-либо значение, тем больше ускоряется его рост. То есть, со временем растет не только значение, но и сама скорость его роста.

А это, иными словами, означает, что значение переменной функции и скорость ее роста находятся в прямо пропорциональной зависимости. То есть, если значение увеличиться два раза, скорость роста увеличится тоже в 2 раза.

В конечном итоге, экспоненциальный рост — самый быстрый.

На самом деле, все вышесказанное касается любой показательной функции, а не только экспоненты.

Основанием может быть любое не отрицательное число, хоть два, хоть три, хоть… сколько угодно.

Несколько примеров из жизни

Самым актуальным и наглядным можно назвать ситуацию с распространением вируса (либо любой другой инфекции). Предположим, что каждый человек в течение дня заражает двух других. Тогда, в первый день у нас будет один инфицированный, во второй — трое. Один старый знакомый и два новых. Каждый из новичков, в свою очередь заразит двух других. В третий день — 7 заразившихся, в четвертый — 1, а пятый — 31… Стоп, это только при условии, что каждый человек заразит только двоих и, чудесным образом, перестанет это делать на притяжении следующих дней. Но ведь так не будет! Все эти люди и дальше будут заражать по 2 человека в день.

А раз так, то на третий день будет уже 9 разносчиков вируса, на пятый — 81, а через неделю по нашему воображаемому городу будет бродить уже 729 зараженных.

Это и будет экспоненциальный рост количества зараженных. Без учета их лечения, карантина или любых других мер, болезнь будет развиваться именно так. Через 10 дней зараженных людей будет уже 59 тысяч человек. Через 15 дней — более 14 миллионов. Просто математика, но какой яркий пример экспоненциального роста?

Легко вывести формулу: 1, 3, 9, 27, 81… это «три» в степени 2, 3 и 4. То есть, показательна функция с основанием 3.

И, хотя в этой формуле в степень возводится не число Эйлера (2,71828….), такой рост тоже называется экспоненциальным.

Еще один пример из биологии: размножение бактерий.

Бактерии размножаются делением. Каждая делится надвое и так далее… Но, конечно, не бесконечно. Предел есть, но об этом чуть позже.

Экспоненциальный рост в экономике

Есть примеры роста по экспоненте и в экономике. Самый интересный — финансовая пирамида. Самый безопасный — Закон Мура.

Первый закон Мура гласит, что количество транзисторов удваивается каждые 2 года. Таким образом и вычислительные мощности компьютера удваиваются каждые два года.

Второй Закон Мура (который сформулировал уже не Гордон Мур) гласит, что стоимость производства микросхем также возрастает экспоненциально из-за усложнения технологий.

Что же касается финансовых пирамид, то основная идея в том, что их рост обусловлен исключительно ростом количества «сектантов» верящих в огромные прибыли или тех, кто верит, что сумеет вовремя «соскочить». Так или иначе, пирамиды всегда рушатся. И вот вопрос, почему?

Но, конечно, рост не может продолжаться бесконечно. В случае с бактериями (и любыми другими организмами, да хоть мышами), наступит время, когда им не хватит пространства и пищи. В случае с микросхемами наступит физический предел скорости передачи данных (мы вряд ли сумеем превысить скорость света). Ну а всевозможные волшебные экономические модели в форме пирамид рано или поздно сталкиваются с той же проблемой, питательная среда в виде легковерных последователей

Логистическая кривая

В реальном мире, не таком идеальном как математика, любой процесс может столкнутся с пределом. В примере роста популяции бактерий или даже крупных животных, это количество ресурсов, которое всегда ограничено. Поэтому, при условии, что ресурсы не бесконечны, процесс развивается по s образной кривой. Сначала стремительно растет, а потом — замедляется.

В пример с вирусом, наступает день, когда большая часть населения уже переболела и выработала антитела (либо была искусственно привита) и вирус больше не может распространяться по экспоненциальному закону. Главный вопрос, можно ли точно предсказать этот день?

Мальтузианская ловушка

С экспонентой связан еще один занимательный экономический эффект — «мальтузианская ловушка». Представьте, что рост населения страны происходит по экспоненциальному закону. Например, каждая пара производит на свет не менее 4 детей, те в свою очередь поступают также. Рано или поздно, количество людей превысит количество пищи, необходимое для нормальной жизни.

Просто потому, что производительность труда физически ограничена (например, количеством плодородных земель), к тому же развитие технологий чаще всего происходит линейно, а экспонента всегда растет быстрее. Получается, что технологическое развитие общества не успевает за ростом населения.

Чем это заканчивается? Кризисом, голодом, войнами за ресурсы. Население уменьшается и все начинается с начала.

Почему это сложно представить?

Нам, людям, сложно себе представить развитие процесса «по экспоненте» потому, что не свойственно так мыслить. Мы привыкли к линейным и циклическим процессам. Они чаще встречаются в нашей жизни: циклические изменения дня и ночи и линейные изменения времени. Это просто и привычно. А вот экспоненциальные процессы встречаются реже.

Тем не менее они есть и игнорировать их опасно. Просто потому, что за этой скоростью нашему разуму сложно угнаться. Даже простые объяснения экспоненциального роста кажутся чем-то абстрактным, а ведь это не выдумка, а наша реальность.

Источник

Экспонента — это. Экспонента простыми словами. Экспоненциальный рост

Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е»‎ ‎– это число Эйлера, которое представляет собой постоянную (

2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.

Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).

Экспонента в жизни. Экспоненциальный рост

Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.

Вирусы . Если представить, что один человек может заразить гриппом еще трех, то число зараженных со временем будет расти по экспоненте. Из одного больного получается четыре, из четырех – двенадцать, и так далее. Именно это и называется экспоненциальным ростом заболеваемости.

Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.

Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.

Употребление пищи . К примеру, когда человек очень голоден, он начинает быстро поглощать пищу. По мере насыщения скорость употребления пищи падает, после чего сводится к нулю.

Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.

Чем экспоненциальный рост отличается от линейного?

Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.

В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.

При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.

Источник