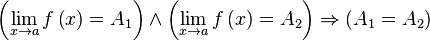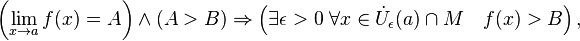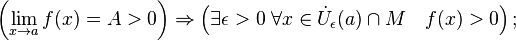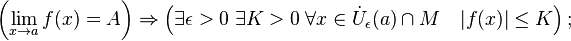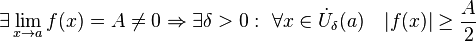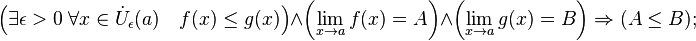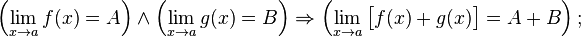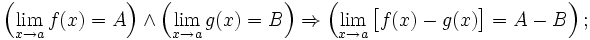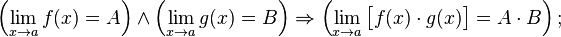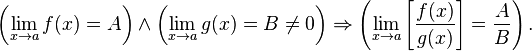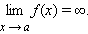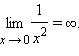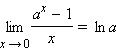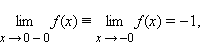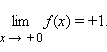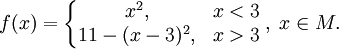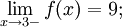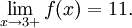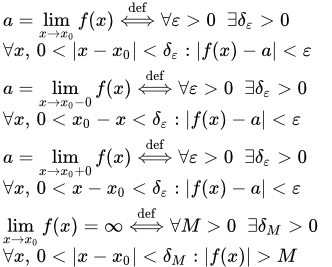- Двусторонний предел функции
- Свойства предала функции
- Определение предела функции в конечной точке
- Определение предела функции по Коши
- Конечный предел функции в конечной точке
- Односторонние пределы
- Бесконечный предел функции в конечной точке
- Определение предела функции по Гейне
- Примеры
- Пример 1
- Пример 2
- Пример 3
Двусторонний предел функции
Помогите пожалуйста разобраться с двусторонними пределами функции.
Допустим есть
у этой дроби в точках +/- бесконечный разрыв и ветки асимптот уходят в +/- бесконечность.
Я начал вычислять пределы и запутался
+бесконечность
т.е. асимптота уходит вверх если идем по функции слева к
здесь идем справа к и ветка уходит вниз
Теперь самое главное — а как понять вычисляя предел в этой точке куда уходит ветка? В + или — бесконечность.
Пока разбираю аналитически — вычисляя пределы последними, когда уже известно в каких точках функция убывает и возрастает.
ПС построил мой пример на десмосе для наглядности
https://www.desmos.com/calculator/ussa5o8mfc
Предел функции.Эквивалентность или Второй замечательный предел?
Ребята,подскажите,не знаю как решить правильно. \lim_
Найти предел функции через замечательный предел
\lim_
Предел последовательности и предел функции
Подскажите пожалуйста как найти эти пределы 1) а) \lim_
Найти предел функции. Исследовать точки разрыва функции
решите эти примеры с подробными обьяснениями плз.Хочу понять как решать эти примеры
Источник
Свойства предала функции
Пусть даны функции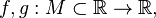 
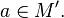
и 
.
· Одна и та же функция в одной и той же точке может иметь только один предел.
Доказательство [показать]
· Сходящаяся функция локально сохраняет знак. Более обще,
где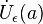 
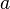
— проколотая окрестность точки 
.
· В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
· Сходящаяся функция локально ограничена в окрестности предельной точки:
· Отделимость от нуля функций, имеющих предел, отличный от нуля.
· Операция взятия предела сохраняет нестрогие неравенства.
· Правило двух милиционеров
· Предел суммы равен сумме пределов:
· Предел разности равен разности пределов:
· Предел произведения равен произведению пределов:
· Предел частного равен частному пределов.
Бесконечные пределы в конечной точке
Кроме конечных пределов существуют и бесконечные.
Функцияf(x), определенная в некоторой окрестности точки а из множества действительных чисел, кроме, быть может, самой точкиа, имеет в этой точке бесконечный предел, если для каждогоε > 0найдется такая δ —окрестность точкиа, что всех х, удовлетворяющих условию 0 ε.
В этом случае записывают: 
Функцию f(x) принято называть бесконечно большой при х → а, а прямуюх = а — вертикальной асимптотой.
Пример. Рассмотрим функцию
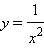
Эта функция определена при х ≠ 0. Если х → 0, то| f(x) |неограниченно возрастает, т.е. 
Предел в бесконечности
Число А называется пределом функции f(x) приx → + ∞ , если для каждого ε > 0 существует такое δ > 0, что всехx > δвыполняется неравенство | f (x) – A | 0 существует такое δ > 0, что всех x 0 существует такое δ > 0, что всех | x | > δвыполняется неравенство| f (x) – A | 0, a ≠ 1):
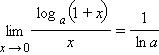
Односторонние пределы
Пусть задано а — действительное число.
Число А1 является пределом слева функции f(x) в точке а, для любогоε > 0 существует δ > 0 такое, что для любогоxиз интервала ( а —δ ; а)выполняется неравенство| f( x ) — A1| 0 существует δ >0такое, что для любого x из интервала ( а; а + δ) выполняется неравенство| f( x ) — A2|
ЧислаА1и А2принято называть односторонними пределами.Эти пределы характерезуют поведение функции справа и слева от точки А.
Из всего сказанного выше получается,что функция f(x)имеет предел в точке а из множества действительных чисел тогда и только тогда, когда в этой точке она имеет односторонние пределы и эти пределы совпадают.
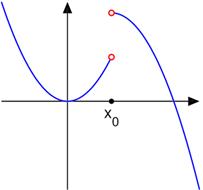
Приведем пример, когда односторонние пределы не совпадают. Тогда говорят, что предела в рассматриваемой точке нет.
Пусть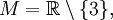 
и задана функция
Рассмотрим график заданной функции
Установили, что в точке х0= 3односторонние пределы не совпадают. Следовательно, предела рассматриваемой функции в точке х0= 3 не существует.
. Критерий существования двустороннего предела :
Двухсторонний предел существует если существуют и равны между собой односторонние пределы .
Источник
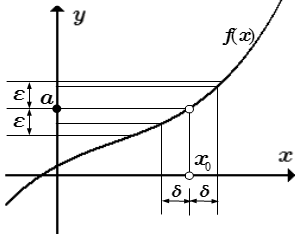
Определение предела функции в конечной точке
Определение предела функции по Коши
Конечный предел функции в конечной точке
Определение конечного предела функции по Коши
Число a называется пределом функции f ( x ) в точке x 0 , если
1) существует такая проколотая окрестность конечной точки x 0 , на которой функция определена;
2) для любого сколь угодно малого положительного числа ε > 0 существует такое число δε > 0 , зависящее от ε , что для всех x , принадлежащих проколотой δε — окрестности точки x 0 : 0 |x – x 0 | , значения функции принадлежат ε — окрестности точки a :
|f ( x ) – a| .
Предел функции обозначается так:
.
Или при .
С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.
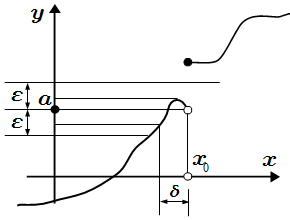
Односторонние пределы
Функция может быть определена не с двух сторон от точки , а в некоторой левой окрестности точки , при или в некоторой правой окрестности, при . Также функция может иметь разрыв в точке . Тогда используют односторонние пределы.
Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .
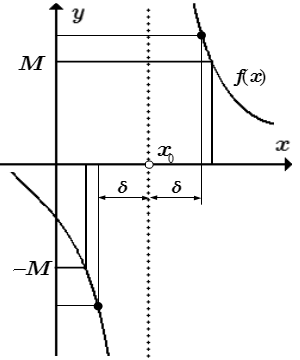
Бесконечный предел функции в конечной точке
Определение бесконечного предела функции по Коши
Предел функции f ( x ) при x → x 0 равен бесконечности, если
1) существует такая проколотая окрестность конечной точки x 0 , на которой функция определена;
2) для любого, сколь угодно большого числа M > 0 , существует такое число δM > 0 , зависящее от M , что для всех x , принадлежащих проколотой δM — окрестности точки x 0 : 0 |x – x 0 | , значения функции принадлежат окрестности бесконечно удаленной точки:
|f ( x ) | > M .
Бесконечный предел обозначают так:
.
Или при .
С помощью логических символов существования и всеобщности определение бесконечного предела функции можно записать так:
.
Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.
Аналогичным образом вводятся определения односторонних пределов.
Левые пределы.
.
.
.
Правые пределы.
.
.
.
Определение предела функции по Гейне
Число a (конечное или бесконечно удаленное) называется пределом функции f ( x ) в точке x 0 :
,
если
1) существует такая проколотая окрестность точки x 0 , на которой функция определена;
2) для любой последовательности < xn > , сходящейся к x 0 : ,
элементы которой принадлежат окрестности , последовательность < f ( xn )> сходится к a :
.
Если в качестве окрестности взять левостороннюю окрестность точки x 0 , то получим определение левого предела. Если правостороннюю – то получим определение правого предела.
Определения предела по Гейне и Коши эквивалентны.
Примеры
Все примеры Далее мы приводим подробные решения задач, в которых нужно показать существование пределов, используя определение предела по Коши.
⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Используя эпсилон и дельта — рассуждения показать, что
.
Введем обозначения:
.
Выпишем определение конечного предела функции в точке по Коши:
.
Преобразуем разность:
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 2
Все примеры ⇑ Используя определение предела по Коши показать, что
.
Введем обозначение:
.
Выпишем определение предела функции в точке , равного бесконечности, по Коши:
.
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 3
Все примеры ⇑ Используя определение предела по Коши показать, что
.
Введем обозначение:
.
Выпишем определение левого предела в точке , равного , по Коши:
.
В нашем случае .
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов . Опубликовано: 12-05-2018
Источник
