Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
Условие задачи:
Стержень длины \(L\) движется по гладкой горизонтальной поверхности. Какая упругая сила возникает в сечении стержня на расстоянии \(L/4\) от конца, к которому приложена сила \(F\), направленная вдоль стержня?
Задача №2.1.83 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
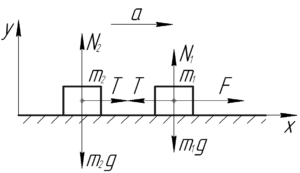
Пусть масса всего стержня \(m\). Так как масса распределена по длине стержня равномерно, то масса брусков, о которых говорится выше, равна соответственно:
Поверхность, по которой скользит стержень, гладкая, значит силы трения отсутствуют. Запишем второй закон Ньютона для брусков в проекции на ось \(x\). Очевидно, что бруски двигаются с одинаковым ускорением (таким же, как и стержень).
Сложим вместе оба этих выражения.
Подставим полученную формулу для ускорения в последнее выражение системы.
Понятно, что \(
Ответ: \(\frac<<3F>><4>\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Что значит движется по гладкой горизонтальной поверхности
По гладкой горизонтальной плоскости XOY (см. рис., вид сверху) равномерно движется маленький шарик со скоростью 5 м/с, направленной под углом к оси OY. Масса шарика 100 г. В точке А шарик абсолютно неупруго сталкивается со стенкой, расположенной вдоль оси ОХ. Чему равен модуль изменения проекции импульса шарика на ось ОХ? Ответ дайте в кг · м/с.
Скорость шарика перед ударом равнялась после абсолютно неупругого удара
Изменение импульса шарика
в проекции на ось ОX:
Тогда
По гладкой горизонтальной плоскости XOY (см. рис., вид сверху) равномерно движется маленький шарик со скоростью 5 м/с, направленной под углом к оси OY. Масса шарика 200 г. В точке А шарик абсолютно неупруго сталкивается со стенкой, расположенной вдоль оси ОХ. Чему равен модуль изменения проекции импульса шарика на ось ОY? Ответ дайте в кг · м/с.
Скорость шарика перед ударом равнялась после абсолютно неупругого удара
Изменение импульса шарика
в проекции на ось ОY:
Тогда
Аналоги к заданию № 19785: 19820 Все
Точечное тело движется вдоль прямой OX по гладкой горизонтальной поверхности. На рисунке изображён график зависимости проекции ax ускорения этого тела от времени t. В момент времени t = 5 с проекция скорости этого тела на ось OX равна 10 м/с. Чему был равен модуль скорости этого тела в момент начала движения при t = 0?
Из графика следует, что проекция ускорения равна При равноускоренном движении проекция скорости равна
Точечное тело движется вдоль прямой OX по гладкой горизонтальной поверхности. На рисунке изображён график зависимости проекции ax ускорения этого тела от времени t. В момент времени t = 5 с проекция скорости этого тела на ось OX равна −10 м/с. Чему был равен модуль скорости этого тела в момент начала движения при t = 0?
Из графика следует, что проекция ускорения равна При равноускоренном движении проекция скорости равна
Аналоги к заданию № 25233: 25270 Все
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 4h (см. рисунок). На правой вершине горки находится шайба. Масса горки в 8 раз больше массы шайбы. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Найдите скорость шайбы на левой вершине горки.
Какие законы Вы используете для описания взаимодействия горки и тела? Обоснуйте их применение к данному случаю.
Обоснование. Горка и тело движутся поступательно. Внешние силы — сила реакции опоры и сила тяжести — не оказывают действия в горизонтальном направлении. Сила трения не действует, т. к. поверхность горки гладкая. Действием силы сопротивления воздуха можно пренебречь. Тогда в инерциальной системе отсчета по горизонтальной оси можно применять закон сохранения импульса.
Суммарная работа силы реакции опоры равна нулю, внешние силы трения и сопротивления не действуют, поэтому в инерциальной системе отсчета применим закон сохранения энергии для системы тел «горка — тело».
Перейдем к решению. На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
здесь и
— скорости шайбы и горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений и используя тот факт, что для скорости шайбы на левой вершине горки получаем
Ответ:
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной
Найдите отношение масс шайбы и горки.
Какие законы Вы используете для описания взаимодействия горки и тела? Обоснуйте их применение к данному случаю.
Обоснование. Горка и тело движутся поступательно. Внешние силы — сила реакции опоры и сила тяжести — не оказывают действия в горизонтальном направлении. Сила трения не действует, т. к. поверхность горки гладкая. Действием силы сопротивления воздуха можно пренебречь. Тогда в инерциальной системе отсчета по горизонтальной оси можно применять закон сохранения импульса.
Суммарная работа силы реакции опоры равна нулю, внешние силы трения и сопротивления не действуют, поэтому в инерциальной системе отсчета применим закон сохранения энергии для системы тел «горка — тело»
Перейдем к решению. На систему тел «шайба — горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
здесь — скорость горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений, отношение масс шайбы и горки получаем
Ответ:
Горка с двумя вершинами, высоты которых h и покоится на гладкой горизонтальной поверхности стола (см. рисунок). На правой вершине горки находится монета. От незначительного толчка монета и горка приходят в движение, причём монета движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. В некоторый момент времени монета оказалась на левой вершине горки, имея скорость
Найдите скорость горки в этот момент.
Какие законы Вы используете для описания взаимодействия горки и тела? Обоснуйте их применение к данному случаю.
Обоснование. Горка и тело движутся поступательно. Внешние силы — сила реакции опоры и сила тяжести — не оказывают действия в горизонтальном направлении. Сила трения не действует, т. к. поверхность горки гладкая. Действием силы сопротивления воздуха можно пренебречь. Тогда в инерциальной системе отсчета по горизонтальной оси можно применять закон сохранения импульса.
Суммарная работа силы реакции опоры равна нулю, внешние силы трения и сопротивления не действуют, поэтому в инерциальной системе отсчета применим закон сохранения энергии для системы тел «горка — тело».
Перейдем к решению. На систему тел «монета + горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
здесь — скорость горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений, для скорости горки получаем
Ответ:
Горка с двумя вершинами, высоты которых h и 3h, покоится на гладкой горизонтальной поверхности стола (см. рисунок). На правой вершине горки находится шайба, масса которой в 12 раз меньше массы горки. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Найдите скорость горки в тот момент, когда шайба окажется на левой вершине горки.
Какие законы Вы используете для описания взаимодействия горки и тела? Обоснуйте их применение к данному случаю.
Обоснование. Горка и тело движутся поступательно. Внешние силы — сила реакции опоры и сила тяжести — не оказывают действия в горизонтальном направлении. Сила трения не действует, т. к. поверхность горки гладкая. Действием силы сопротивления воздуха можно пренебречь. Тогда в инерциальной системе отсчета по горизонтальной оси можно применять закон сохранения импульса.
Суммарная работа силы реакции опоры равна нулю, внешние силы трения и сопротивления не действуют, поэтому в инерциальной системе отсчета применим закон сохранения энергии для системы тел «горка — тело»
Перейдем к решению. На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
Здесь и
— скорости шайбы и горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений и используя тот факт, что для скорости шайбы на левой вершине горки получаем
Ответ:
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.
Какие законы Вы используете для описания взаимодействия горки и тела? Обоснуйте их применение к данному случаю.
Обоснование. Горка и тело движутся поступательно. Внешние силы — сила реакции опоры и сила тяжести — не оказывают действия в горизонтальном направлении. Сила трения не действует, т. к. поверхность горки гладкая. Действием силы сопротивления воздуха можно пренебречь. Тогда в инерциальной системе отсчета по горизонтальной оси можно применять закон сохранения импульса.
Суммарная работа силы реакции опоры равна нулю, внешние силы трения и сопротивления не действуют, поэтому в инерциальной системе отсчета применим закон сохранения энергии для системы тел «горка — тело».
Перейдем к решению. На систему тел «шайба — горка» действуют внешние силы (тяжести и реакции стола), но они обе направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется.
В начальный момент в конечный момент проекция полного импульса равна
Из закона сохранения импульса получим:
где m — масса шайбы, M — масса горки.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решение системы даёт отношение масс
Ответ:
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рисунок). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.
Обоснование. Трубка находится на гладком столе, т. е. отсутствует сил трения. Поверхность трубки гладкая, следовательно, на шарик не действует сила трения. В инерциальной системе отсчета при взаимодействии трубки и шарика можно применять закон сохранения импульса. Внешние силы тяжести и реакции опоры можем не учитывать при рассмотрении изменения скорости тел в горизонтальном направлении. По тем же причинам система «трубка-шарик» является замкнутой, поэтому в инерциальной системе отсчета применим закон сохранения энергии.
Перейдем к решению.
1. Из условия задачи следует, что шарик вылетит из трубки с некоторой скоростью относительно стола, а брусок приобретёт горизонтальную скорость
направленную влево (см. рисунок).
2. Поскольку шарик в системе отсчёта, связанной с бруском, вылетает вдоль трубки со скоростью направленной под углом
к горизонту, а сама трубка в момент вылета шарика движется влево со скоростью
согласно классическому закону сложения скоростей имеем:
и и по теореме косинусов
3. Поскольку механическая энергия системы сохраняется, то можно записать:
4. Сохраняется также и нулевая горизонтальная проекция импульса системы, так что
5. Решая полученную систему уравнений, находим модуль искомой скорости бруска:
м/с.
Ответ: м/с.
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 4h (см. рисунок). На правой вершине горки находится шайба. Масса горки в 8 раз больше массы шайбы. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Найдите скорость шайбы на левой вершине горки.
На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
здесь и
— скорости шайбы и горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений и используя тот факт, что для скорости шайбы на левой вершине горки получаем
Ответ:
Можно поподробнее, каким образом энергия кинетическая горки связана с энергией потенциальной шайбы, ведь корка приобретает скорость от толчка (пожалуйста)?
«От незначительного толчка шайба и горка приходят в движение» — импульсом, полученным от толчка, пренебрегаем. Шайба и горка приобретают скорость, взаимодействуя друг с другом.
Вторая (малая) горка движется на встречу шайбе, а шайба при этом движется на встречу второй горке. Надо же рассматривать закон сохранения импульса между шайбой и второй (малой) горкой?
Горки не отдельные. Ошибки нет.
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной
Найдите отношение масс шайбы и горки.
На систему тел «шайба — горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
здесь — скорость горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений, отношение масс шайбы и горки получаем
Ответ:
Горка с двумя вершинами, высоты которых h и покоится на гладкой горизонтальной поверхности стола (см. рисунок). На правой вершине горки находится монета. От незначительного толчка монета и горка приходят в движение, причём монета движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. В некоторый момент времени монета оказалась на левой вершине горки, имея скорость
Найдите скорость горки в этот момент.
На систему тел «монета + горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
здесь — скорость горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений, для скорости горки получаем
Ответ:
Горка с двумя вершинами, высоты которых h и 3h, покоится на гладкой горизонтальной поверхности стола (см. рисунок). На правой вершине горки находится шайба, масса которой в 12 раз меньше массы горки. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Найдите скорость горки в тот момент, когда шайба окажется на левой вершине горки.
На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), но они направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется. В начальный момент времени импульс системы равен нулю, поэтому для интересующего нас момента времени, можно написать:
Здесь и
— скорости шайбы и горки относительно горизонтальной поверхности.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решая систему из этих двух уравнений и используя тот факт, что для скорости шайбы на левой вершине горки получаем
Ответ:
почему не учитывается масса шайбы при движении горки? мы считаем, что должно быть М+m вместо М
Все скорости относительно неподвижной системы отсчета. В решении есть импульс и энергия для горки и для шайбы, так что ничто не забыто
почему в конечной формуле в знаменателе получается 39? У меня просто 9
На гладкой горизонтальной плоскости находятся две одинаковые идеально упругие гладкие шайбы. Одна из них движется со скоростью равной по модулю 2 м/с, а другая покоится вблизи прямой линии, проведённой через центр первой шайбы в направлении её скорости. Шайбы сталкиваются, и после соударения вторая, первоначально покоившаяся шайба отскакивает под углом α = 45° к этой линии. Найдите скорость
первой шайбы после столкновения.
Какие законы Вы используете для описания взаимодействия шайб? Обоснуйте их применение к данному случаю.
Обоснование. Поверхности, по которым движутся шайбы, гладкие. Следовательно, внешние силы сопротивления не действуют. Внешние силы реакции опоры и силы тяжести не оказывают действия в горизонтальном направлении. Следовательно, в инерциальной системе отсчета применим закон сохранения импульса.
При абсолютно упругом ударе шайб нет потерь энергии. В инерциальной системе отсчета применим закон сохранения энергии для системы двух шайб.
Перейдем к решению. При идеально упругом столкновении шайб сохраняются их импульс и кинетическая энергия. Поскольку шайбы одинаковые, эти законы сохранения имеют следующий вид:
где — скорость второй шайбы после столкновения. По обратной теореме Пифагора отсюда следует, что векторы
и
взаимно перпендикулярны, и первая шайба, как и вторая, отскакивает также под углом
к линии своего первоначального движения.
Из первого уравнения следует, что проекция импульса системы из двух шайб на направление, перпендикулярное линии первоначального движения первой шайбы, равна нулю:
откуда Тогда из второго уравнения получаем, что
Ответ: Скорость первой шайбы равна по модулю и направлена под углом
отсчитанным от линии первоначального движения, в другую сторону по отношению к углу отскока второй шайбы.
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.
На систему тел «шайба — горка» действуют внешние силы (тяжести и реакции стола), но они обе направлены по вертикали, поэтому проекция импульса системы на горизонтальную ось Оx системы отсчёта, связанной со столом, сохраняется.
В начальный момент в конечный момент проекция полного импульса равна
Из закона сохранения импульса получим:
где m — масса шайбы, M — масса горки.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
Решение системы даёт отношение масс
Ответ:
в законе сохранения импульса не
учитывается масса шайбы mv=(M+m)u
шайба находится на горке и движется вместе с ней. То же самое можно сказать и о законе сохранения энергии.
Скорости берутся относительно горизонтальной поверхности.
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рисунок). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
1. Из условия задачи следует, что шарик вылетит из трубки с некоторой скоростью относительно стола, а брусок приобретёт горизонтальную скорость
направленную влево (см. рисунок).
2. Поскольку шарик в системе отсчёта, связанной с бруском, вылетает вдоль трубки со скоростью направленной под углом
к горизонту, а сама трубка в момент вылета шарика движется влево со скоростью
согласно классическому закону сложения скоростей имеем:
и и по теореме косинусов
3. Поскольку механическая энергия системы сохраняется, то можно записать:
4. Сохраняется также и нулевая горизонтальная проекция импульса системы, так что
5. Решая полученную систему уравнений, находим модуль искомой скорости бруска:
м/с.
Ответ: м/с.
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рисунок). Общая масса бруска с трубкой равна M = 1 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 1 м над бруском, опускают без начальной скорости маленький шарик массой m = 100 г. Другой конец трубки наклонён к горизонту под углом α = 45° и находится на высоте h = 30 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
1. Из условия задачи следует, что шарик вылетит из трубки с некоторой скоростью относительно стола, а брусок приобретёт горизонтальную скорость
направленную влево (см. рисунок).
2. Поскольку шарик в системе отсчёта, связанной с бруском, вылетает вдоль трубки со скоростью направленной под углом
к горизонту, а сама трубка в момент вылета шарика движется влево со скоростью
согласно классическому закону сложения скоростей имеем:
и по теореме косинусов
3. Поскольку механическая энергия системы сохраняется, то можно записать:
4. Сохраняется также и нулевая горизонтальная проекция импульса системы, так что
5. Решая полученную систему уравнений, находим модуль искомой скорости бруска:
м/с.
Ответ: м/с.
Аналоги к заданию № 9072: 9227 Все
На гладкой горизонтальной плоскости лежат два груза массами и
соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.
Какие законы Вы используете для описания движения брусков? Обоснуйте их применение.
Обоснование. Бруски движутся поступательно. Следовательно, их можно считать материальными точками. Подвижный блок невесом. На каждый брусок действуют сила тяжести и сила натяжения нити. На гладкой поверхности и в блоках отсутствует сила трения. Поэтому для описания движения каждого бруска по горизонтальной поверхности в инерциальной системе отсчета под действием этой силы с ускорением можно применять второй закон Ньютона.
Нить невесома. Значит, силы натяжения нити, действующая на каждый брусок и на подвижный блок, имеет одинаковое по модулю значения.
Нить нерастяжима. Поэтому можно составить уравнение кинематической связи между ускорениями брусков и подвижного блока.
Перейдем к решению. Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:
В силу невесомости блока О имеем или
В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты xA и xB постоянны) имеется следующая кинематическая связь между координатами и
грузов и координатой
блока О (здесь r — радиус блоков А и В, R — радиус блока О):
Решаем записанную систему уравнений и получаем ответ:
Ответ:
На гладкой горизонтальной плоскости лежат два груза массами и
соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена некоторая направленная вертикально вниз сила, в результате чего ось О движется с ускорением
Найдите модуль F этой силы. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.
Какие законы Вы используете для описания движения брусков? Обоснуйте их применение.
Обоснование. Бруски движутся поступательно. Следовательно, их можно считать материальными точками. Подвижный блок невесом. На каждый брусок действуют сила тяжести и сила натяжения нити. На гладкой поверхности и в блоках отсутствует сила трения. Поэтому для описания движения каждого бруска по горизонтальной поверхности в инерциальной системе отсчета под действием этой силы с ускорением можно применять второй закон Ньютона.
Нить невесома. Значит, силы натяжения нити, действующая на каждый брусок и на подвижный блок, имеет одинаковое по модулю значения.
Нить нерастяжима. Поэтому можно составить уравнение кинематической связи между ускорениями брусков и подвижного блока.
Перейдем к решению. Нарисуем силу F и силы T натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок O (см. рисунок). Введем систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось
В силу невесомости блока O имеем или
В силу нерастяжимости нити (длиной L) и неподвижности блоков A и B (их координаты xA и xB постоянны) имеется следующая кинематическая связь между координатами и
грузов и координатой
блока O (здесь r — радиус блоков A и
— радиус блока O:
Решаем записанную систему уравнений и получаем ответ:
откуда
Ответ:
Источник


