Что значит две смежные стороны равны

Признаки равенства треугольников

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

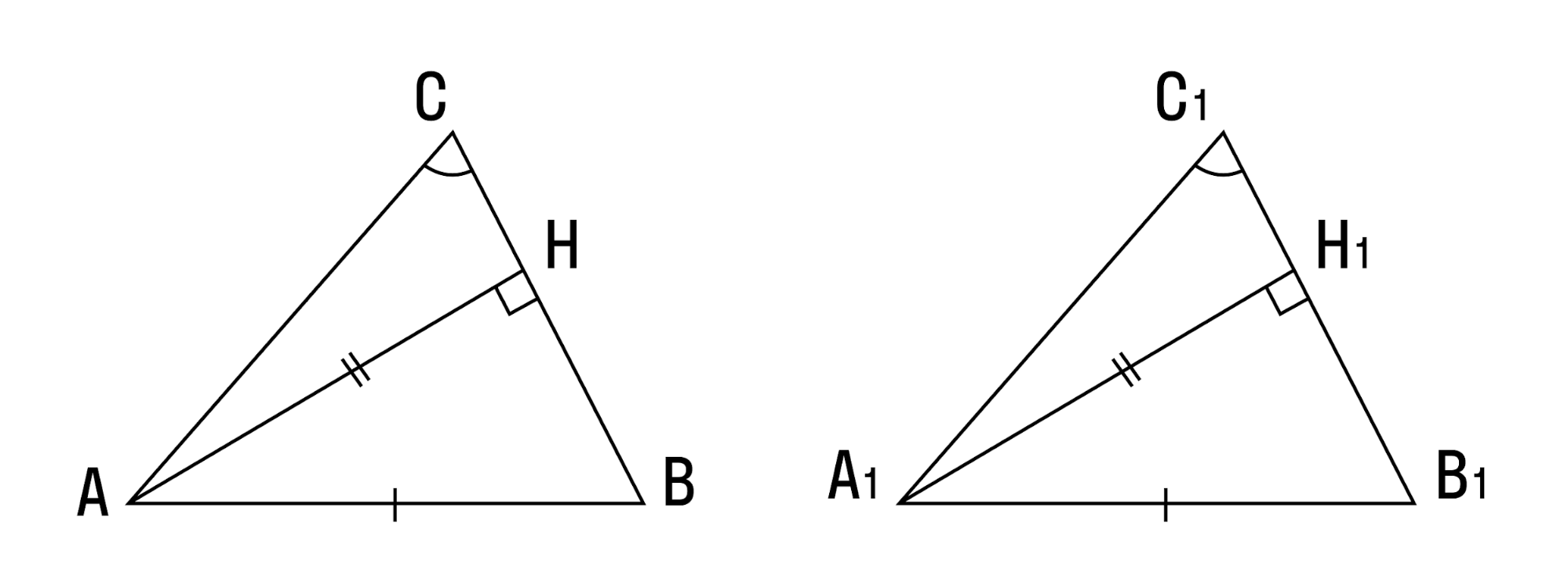
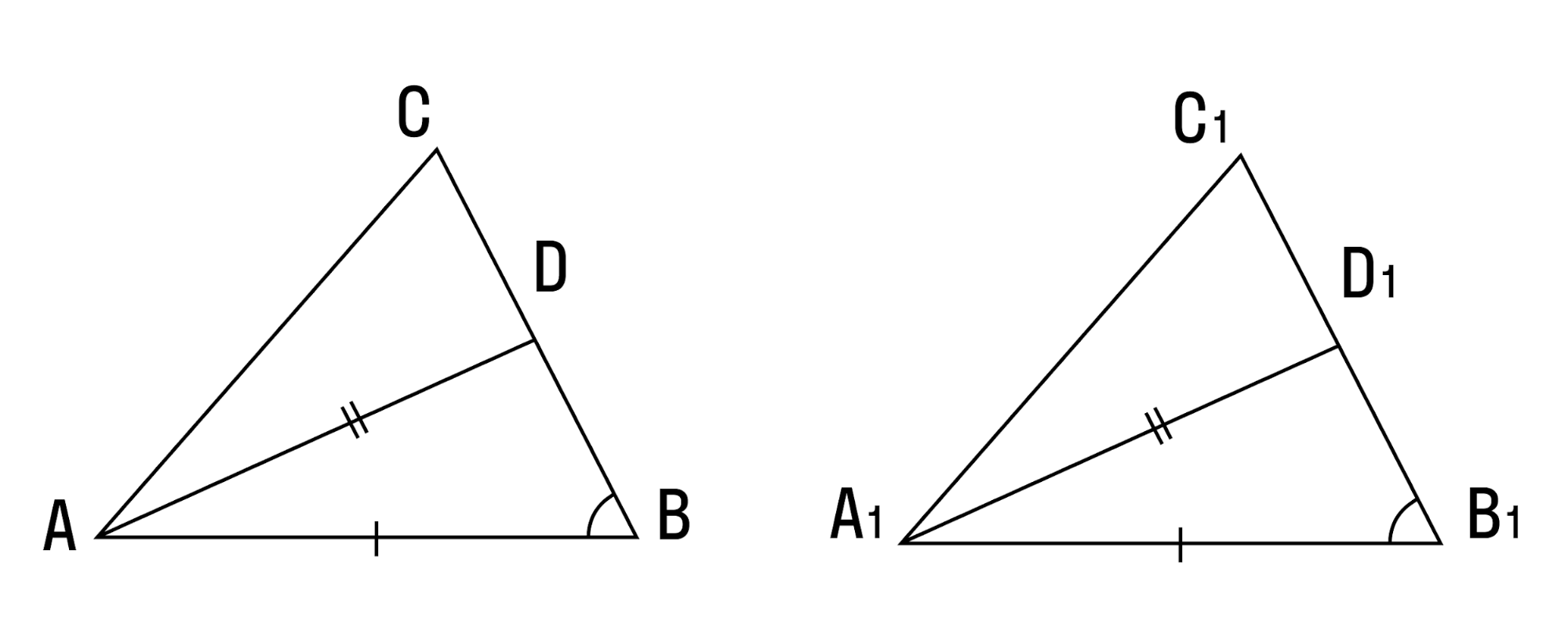
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
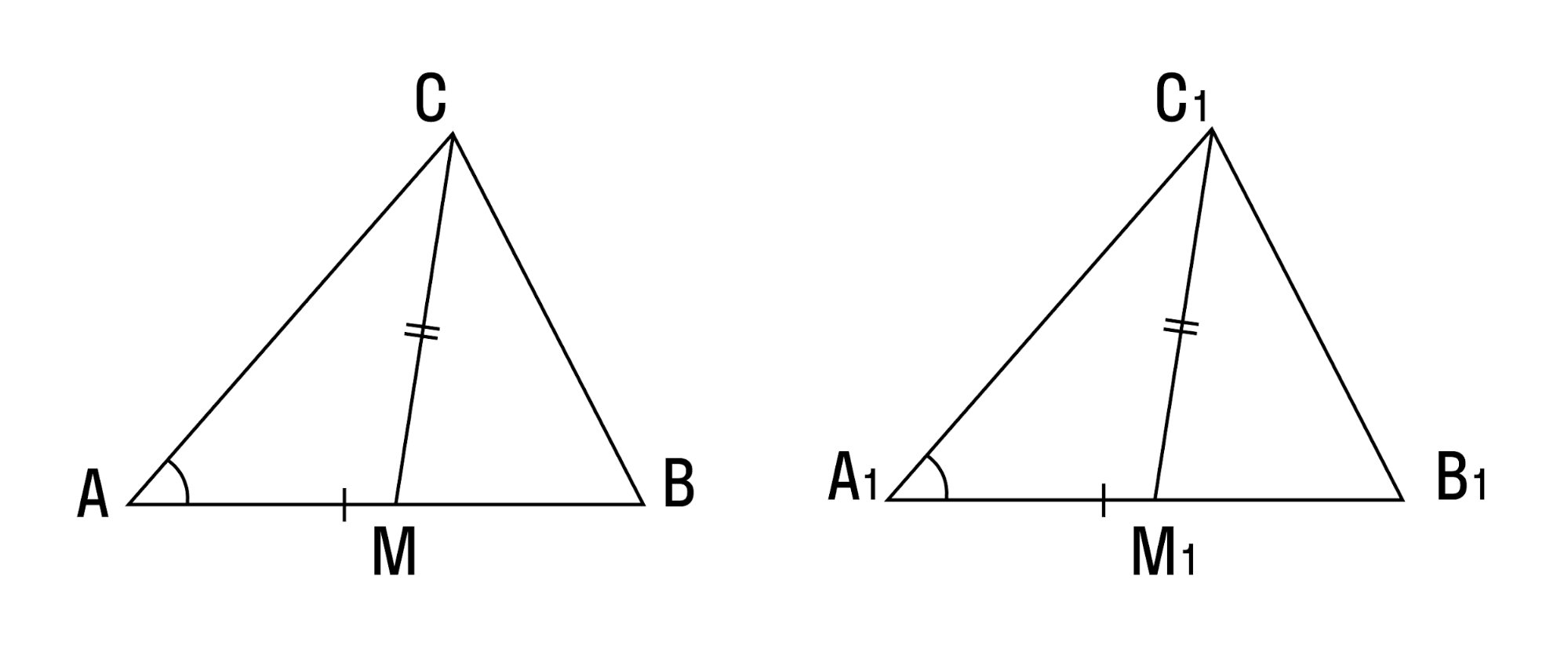
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
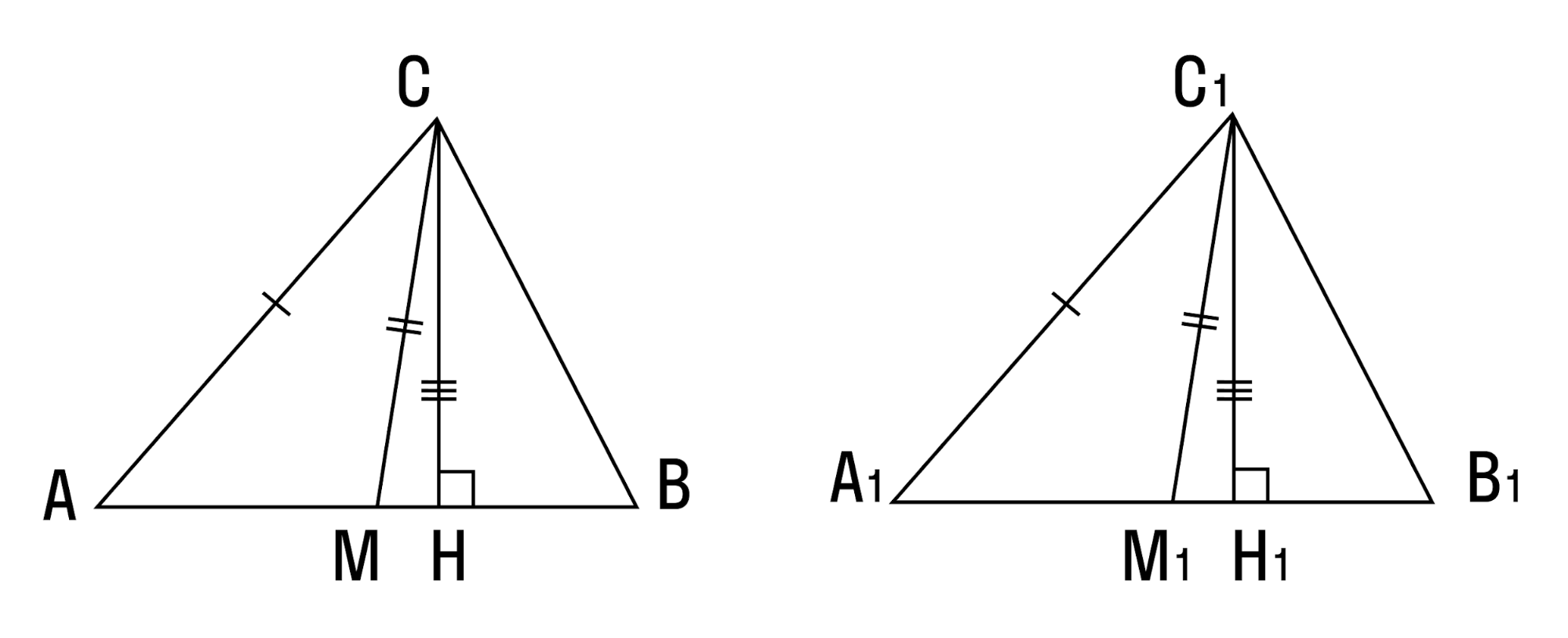
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Смежные углы. Свойства смежных углов

Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.

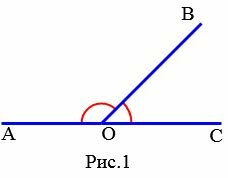На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:

.

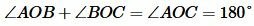(1)

Свойства смежных углов

1. Сумма смежных углов равна 180°

2. Если оба смежных угла равны между собой, то они являются прямыми.

3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.

4. Синусы смежных углов равны.

5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.

Справедливость пунктов 2 и 3 очевидны и следуют из (1).

Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)

.

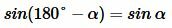То есть синусы смежных углов равны.

Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но

,

,

.

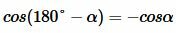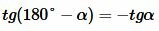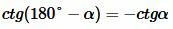То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Источник

Признаки равенства прямоугольников

Признаки равенства прямоугольников — это признаки, c
помощью которых можно доказать, что прямоугольники равны.

В этой статье мы рассмотрим и докажем четыре признака
равенства прямоугольников. С помощью этих признаков
можно доказать, равенство двух и более геометрических
фигур — в данном случае прямоугольников.

I признак равенства прямоугольников

Формулировка первого признака равенства
прямоугольников:

Если две неравных стороны одного прямоугольника
соответственно равны двум неравным сторонам другого
прямоугольника, то такие прямоугольники равны.

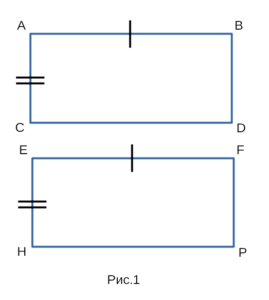
Докажем, что прямоугольники ABDC и EFPH,
изображенные на рисунке 1 равны между собой.

Доказательство первого признака равенства
прямоугольников:

1. Рассмотрим прямоугольники ABDC и EFPH, в которых
   AB = EF, AC = EH. Докажем, что прямоугольники
   ABDC и EFPH равны.
2. AB = EF, значит сторону AB можно наложить на сторону
   EF так, что сторона AB совместится со стороной EF.
3. AC = EH, значит сторону AC можно наложить на сторону
   EH так, что сторона AC совместится со стороной EH.
4. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

II признак равенства прямоугольников

По сумме квадратов двух неравных сторон.

Формулировка второго признака равенства
прямоугольников:

Если сумма квадратов двух неравных сторон одного прямоугольника
соответственно равна сумме квадратов двух неравных сторон
другого прямоугольника, то они равны.

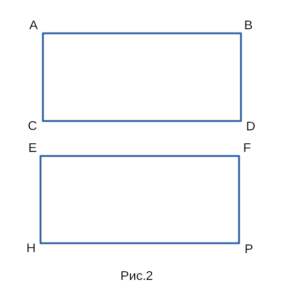
Докажем, что прямоугольники ABDC и EFPH, изображенные
на рисунке 2 равны между собой.

Доказательство второго признака равенства
прямоугольников:

1. Рассмотрим ABDC и EFPH, в которых AB² + ВD² = EF² + FP².
   Докажем, что прямоугольники ABDC и EFPH равны.
2. AB ²+ ВD² = EF² + FP², значит стороны AB и BD можно наложить
   на стороны EF и FP, так что: сторона AB совместится со стороной EF,
   сторона BD совместится со стороной FP.
3. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

III признак равенства прямоугольников

По диаметру описанной окружности.

Формулировка третьего признака равенства
прямоугольников:

Если диаметр описанной окружности одного прямоугольника
соответственно равен диаметру описанной окружности другого
прямоугольника, то такие прямоугольники равны.

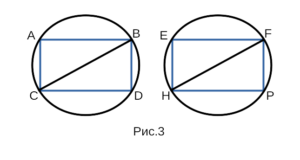
Докажем, что прямоугольники ABDC и EFPH, изображенные
на рисунке 3 равны между собой.

Доказательство третьего признака равенства
прямоугольников:

1. Рассмотрим ABDC и EFPH, в которых CB = HE. Докажем,
   что прямоугольники ABDC и EFPH равны.
2. CB = HE, значит диаметры СВ и HE можно наложить друг
   на друга так, что они совместятся: диаметр СВ совместится
   с диаметром HE.
3. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

IV признак равенства прямоугольников

По равным и параллельным противоположным сторонам.

Формулировка четвертого признака равенства
прямоугольников:

Если противоположные стороны одного прямоугольника соответственно
параллельны и равны противоположным сторонам другого прямоугольника,
то такие прямоугольники равны.

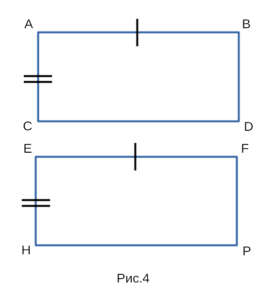
Докажем, что прямоугольники ABDC и EFPH, изображенные
на рисунке 4 равны между собой.

Доказательство четвертого признака равенства
прямоугольников:

1. Рассмотрим прямоугольники ABDC и EFPH, в которых
   AB = EF, AC = EH и AB ∥ EF, AC ∥ EH. Докажем, что
   прямоугольники ABDC и EFPH равны.
2. AB = EF и AB ∥ EF, значит сторону AB можно наложить на
   сторону EF так, что сторона AB совместится со стороной EF.
3. AC = EH и AC ∥ EH, значит сторону AC можно наложить на
   сторону EH так, что сторона AC совместится со стороной EH.
4. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

В этой статье мы доказали равенство прямоугольников по всем четырем признакам.

• Двум неравным сторонам.
• Сумме квадратов двух неравных сторон.
• Диаметру описанной окружности.
• Равным и параллельным противоположным сторонам.

Источник

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Равнобедренным называется треугольник, у которого две стороны равны.

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Для доказательства следующих теорем нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

В каждом из доказательств мы пользуемся признаком равенства треугольников, вот и повод их повторить.

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Свойства углов равнобедренного треугольника В равнобедренном треугольнике углы при основании равны. Углы при основании в равнобедренном треугольнике — всегда острые.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Источник