Проверка однородности дисперсий
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия.
Если полученное значение дисперсионного отношения больше приведенного в таблице для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы
,
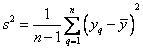
а затем из всех дисперсий находится наибольшая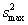 
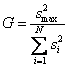
которая делится на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий
.
Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превышает табличного значения. Тогда можно усреднять дисперсии и пользоваться формулой
.
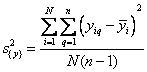
Если возникает предположение о наличии неоднородности дисперсий для случая, когда число повторных опытов неодинаково во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой формуле подсчитывается дисперсия воспроизводимости
.
Далее находится величина
,
.
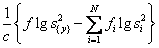
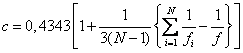
Здесь число степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании эксперимента типа 2 k это число равно числу опытов в матрице.
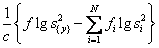
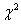
Бартлет показал, что величина приближенно подчиняется 
– распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.
Критерий Бартлета базируется на нормальном распределении. Если имеются отклонения от нормального распределения, то проверка неоднородности дисперсий может привести к ошибочным результатам.
Можно предложить использование F-критерия даже в тех случаях, когда число дисперсий больше двух. Делается это следующим образом. Из всех дисперсий выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дисперсий можно считать принадлежащей к единой совокупности. В таких случаях нет надобности применять критерий Бартлета.
Источник
Большая Энциклопедия Нефти и Газа
Однородность — дисперсия
Однородность дисперсий исследовали по критерию Кохрсна ( G), который равен отношению максимальной дисперсии ах к сумме всех дисперсий V Sf. Дисперсии однородны, если G не превышает табличного значения. Расчет показал, что требование однородности дисперсий выполняется с вероятностью Р 0 95 ( GnKCn. [1]
Однородность дисперсий при одинаковом числе степеней свободы проверяют по критерию Кохрена, а при разном — по критерию Бартлета. Определенная по параллельным опытам дисперсия воспроизводимости s2BOcnp необходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту. [2]
Однородность дисперсий позволяет вычислить средние дисперсии по группе тензорезисторов. Эти дисперсии, полученные для ряда фиксированных значений влияющей или измеряемой величины, характеризуют зависимость погрешности измерения от этой величины. Если средние дисперсии значимо различаются между собой, то это означает, что случайные погрешности средств измерений должны быть определены в зависимости от значений влияющей или измеряемой величины. Однородность средних дисперсий позволяет найти значение случайной погрешности, общее для всех значений влияющей или измеряемой величины. [3]
Однородность дисперсий при одинаковом числе степеней свободы проверяют по критерию Кохрена, а при разном — по критерию Бартлета. Определенная по параллельным опытам дисперсия воспроизводимости оспрнеобходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту. [4]
Однородность дисперсий может быть нарушена, если мы объединим в одну совокупность пробы, в которых концентрация определяемого компонента изменяется в очень широких пределах. В этом случае рекомендуется производить преобразование наблюдений с помощью функции y lgx. Относящиеся сюда примеры будут рассмотрены в § 3 этой главы ( теоретическое обоснование этого метода обсуждалось на стр. [5]
Однородность дисперсий при одинаковом числе степеней свободы проверяют по критерию Кохрена, а при разном — по критерию Бартлета. Определенная по параллельным опытам дисперсия воспроизводимости 52воспр необходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту. [6]
Однородность дисперсии воспроизводимости устанавливается с помощью критерия Фишера. Для этого из вычисленных всех дисперсий ошибок выделяются наибольшая и наименьшая. [7]
Однородность взвешенных дисперсий сигнала подтверждена при аттестации методики. [8]
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера ( F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерня ( см. стр. [9]
Проверка однородности дисперсий в эксперименте производится с помощью G-критерия Кохрена. [10]
Требование однородности дисперсий является одним из требований регрессионного анализа, и поэтому проверке однородности дисперсий следует уделять должное внимание. [11]
Гипотеза об однородности дисперсий принимается. [12]
Гипотезу об однородности дисперсий можно проверить по числу Кохрена, которое применяют, если во всех точках эксперимента одинаковое число повторных опытов. [13]
Гипотеза об однородности дисперсий проверяется с помощью. [14]
Гипотеза об однородности дисперсий принимается. [15]
Источник
Проверка однородности дисперсий
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия.
Если полученное значение дисперсионного отношения больше приведенного в таблице для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.
Пример 2. Пусть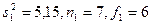 
; 
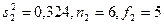
. В данном примере отношение дисперсий равно 5,14/0,324=15,9 при f1=6 и f2=5.
Пользуясь таблицей отношений дисперсий для различных степеней свободы и различного уровня значимости, выбираем наиболее популярный уровень значимости 0,05. В таблице по горизонтали отложены числа степеней свободы для большей дисперсии f1 а по вертикали — числа степеней свободы для меньшей дисперсии f2. Для f1=6 и f2=5 Fта6=4,40. Это значит: вероятность того, что экспериментальное значение F будет больше чем 4,40, равна 0,05 или 5%. Наше Fэксп=15,9. Оно значительно превышает табличное значение.
Так проверяется гипотеза об однородности дисперсий. Наша гипотеза состояла в том, что обе группы экспериментальных данных получены из одной и той же совокупности и дают одинаковое рассеяние. Установили, что одна дисперсия значимо отличается от другой (для выбранного уровня значимости).
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы по формуле 2.1, а затем из всех дисперсий находится наибольшая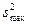 
, которая делится на сумму всех дисперсий. Критерий Кохрена — это отношение максимальной дисперсии к сумме всех дисперсий:
.
С этим критерием связаны числа степеней свободы f1=n—1 и f2=N. Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превышает табличного значения. Тогда можно усреднять дисперсии и пользоваться формулой 2.1.
Пример 3. В начале главы, показывая, как нужно оформлять журнал, мы привели матрицу 2^3 с двумя повторными опытами. Мы сказали: вот с такой таблицей 4.4 можно приступать к обработке экспериментальных данных. Воспользуемся этой таблицей для расчета дисперсии воспроизводимости. Перепишем ее с целью удобства расчета (таблице 2.6).
Таблица 2.6 – Расчет дисперсии воспроизводимости
| Номер опыта | Матрица плани- рования |  |  |  |  |  |  |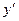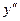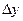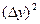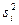
| (1) | 80,23 | 81,93 | 81,08 | -0,85 | 0,722 | 1,144 | |
| a | 86,50 | 84,80 | 85,65 | 0,85 | 0,722 | 1,144 | |
| b | 82,45 | 82,10 | 82,27 | 0,18 | 0,031 | 0,062 | |
| ab | 89,50 | 91,30 | 90,40 | -0,90 | 0,810 | 1,620 | |
| c | 85,10 | 84,80 | 84,95 | 0,15 | 0,023 | 0,046 | |
| ac | 90,30 | 89,60 | 89,95 | 0,35 | 0,123 | 0,246 | |
| bc | 85,60 | 84,90 | 85,25 | 0,35 | 0,123 | 0,246 | |
| abc | 88,02 | 88,48 | 88,25 | -0,23 | 0,053 | 0,106 | |
| Сумма | 2,607 |
Дисперсия в каждом опыте равна:
.
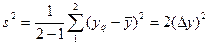
Максимальная дисперсия оказалась в опыте № 4. Экспериментальный критерий Кохрена равен 6=1,620/5,214=0,31. Табличный критерий Кохрена равен: G=0,68. Экспериментальный критерий Кохрена не превышает значения табличного. Гипотеза об однородности дисперсий подтверждается».
Дисперсия воспроизводимости равна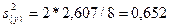 
.
Более экономный вариант проверки однородности основан на выделении из всех дисперсий наибольшей и наименьшей. Затем по F-критерию производится проверка, значимо ли они различаются между собой. Если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дисперсий можно считать принадлежащей к единой совокупности. В таких случаях нет необходимости в применении критерия Бартлета.
Если дисперсии все-таки оказались неоднородными, то оказывается полезным изменение масштаба для параметра оптимизации. При этом вводится некоторая математическая функция от параметра оптимизации, например квадратный корень или логарифм. Использование таких методов выходит за рамки элементарного анализа, и в случае необходимости экспериментатору целесообразно обращаться за советом к специалисту по планированию эксперимента.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Контрольные карты (III). Предварительный анализ: проверка однородности дисперсий.
В предыдущей части в качестве примера мы отобрали данные титриметрического анализа без учёта различий в метрологических характеристиках методик и пришли к выводу о ненормальности распределения вследствие неоднородности данных. Теперь мы распределим сходные методики по группам, и снова убедимся в их принадлежности нормальному распределению. Группирование произведём таким образом: для каждой методики сделаем выборки и установим однородность для каждой выборки по нескольким критериям. Если гипотеза об однородности пройдёт, то мы будем считать, что между метрологическими характеристиками методик нет существенной разницы, и мы можем строить для них общую контрольную карту. Если данные не однородны, то результаты анализов по таким методикам на одну карту наносить не будем.
Примечание. Если метрологические характеристики методов задаются нормативной документацией, то подобный анализ однородности не требуется. Методики просто группируются относительно указанных в НД пределов погрешностей.
В ОСТ 107.460092.001-86 не оговариваются пределы погрешностей, поэтому нам такой анализ потребуется. Отметим, что анализ на однородность данных перед работой с картами в любом случае должен проводиться, но, привязывая анализ к данным групп методик, а не случайных выборок, мы решаем ещё одну задачу — проверяем возможность использования одной контрольной карты для данных полученных от максимально большого количества методик.
В лаборатории при участке гальванопластики реализуется огромное количество методик анализа, но для примера мы рассмотрим данные химического анализа, полученные в ходе выполнения четырёх из них. Первоначально предполагается, что две из них однородны, однородность третьей по отношению к первым двум вызывает сомнение, а четвёртая предположительно не однородна с остальными. Мы проведём анализ однородности, по результатам которого поймём, сколько контрольных карт нужно будет строить для этих четырёх методик анализа (если вдруг все данные окажутся однородными, то достаточно одной контрольной карты; если все данные будут неоднородными, то необходима своя контрольная карта для каждой из методик).
В таблице сведены данные по десяти случайно отобранным химическим определениям. Приведены относительные ошибки определения при 95% доверительной вероятности (εотн., % — х1,х2…х10). Для каждой из выборок была проведена проверка нормальности распределения (расчёты приводить не будем — они аналогичны тем, что мы рассматривали ранее (Контрольные карты (II). Предварительный анализ: проверка принадлежности данных нормальному распределению.), приведём только значения WM-критерия).
Ацидиметрическое определение H 2 SO 4 в электролите лужения
Йодометрическое определение меди в электролите меднения
Комплексонометрическое определение никеля в электролите никелирования
Комплексонометрическое определение свободного кобальта в электролите золочения
Анализ однородности проводится следующим образов:
- Оценивают принадлежность выборок нормальному распределению. Критерии, по которым мы далее будем проверять однородность данных, чувствительны к отклонениям от нормальности распределения.
Этот этап нами уже выполнен (WM-критерий превышает критическое значение WMкр=930).
- Оценивают однородность дисперсий. Данный этап необходим для того, чтобы не ввести себя в заблуждение при оценке средних значений в случае, когда дисперсия у одной из выборок настолько велика, что перекрывает центр распределения второй выборки. Если не провести оценку дисперсий, анализ средних может показать, например, однородность относительных ошибок определения в 2% и в 4% при большой дисперсии второй величины.
- И, наконец, оценивают однородность средних тенденций процессов. Все остальные этапы можно рассматривать как подготовительные к этому.
Рассчитаем средние значения каждой выборки:
x1cредн. = ∑xi1/n1 = (0,52+0,62+0,67+0,72+0,83+0,84+0,87+0,91+1,10+1,29)/10 = 0,84
| Выборка 1 | Выборка 2 | Выборка 3 | Выборка 4 | |
| xcредн. | 0,84 | 0,97 | 1,15 | 2,99 |
| S 2 | 0,0522 | 0,0989 | 0,0689 | 1,1792 |
1) Оценка по критерию Фишера.
Для сравнения двух выборочных дисперсий используют F-критерий. При этом вычисляют отношение большей дисперсии к меньшей:
Затем сравнивают рассчитанное значение Fс табличным Fα(f1,f2), где α – уровень значимости, а f1, f2 – числа степеней свободы для большей и меньшей выборок.
Сравним дисперсии из нашего примера:
| S 2 | 0,0522 | 0,0989 | 0,0689 | 1,1792 |
В нашем случае число степеней свободы для всех выборок одинаковы, поэтому мы найдём отношение максимальной (1,1792) дисперсии к минимальной (0,0522) и сравним его с табличным значением. Если большая и меньшая дисперсия однородны, то все остальные также будут однородны. Если они не будут однородными, то мы найдём отношение второй по величине дисперсии (0,0989) к наименьшей (0,0522) и т.д. Гипотеза об однородности принимается, если F Первая итерация: F = S 2 max/S 2 min= 1,1792/0,0522 = 22,58
Табличное значение Fα=0,05(f1=9,f2=9) = 3,18. Гипотеза отвергается.
Вторая итерация: F= S 2 max/S 2 min= 0,0989/0,0522 = 1,89.
Табличное значение больше расчётного, поэтому гипотеза об однородности дисперсий выборок 1 и 2 принимается. Также однородной с ними является дисперсия выборки 3, т.к. она занимает промежуточное положение.
Подтвердим полученные результаты с помощью критериев Кохрена и Бартлетта (хи-квадрат).
2) Оценка по критерию Кохрена.
Критерий Кохрена применяется для выборок одинакового объёма. В случае использования критерия Кохрена вычисляют отношение максимальной дисперсии к сумме всех дисперсий и сравнивают его с табличным значением:
Если G>Gα(f,n), то принимают гипотезу об отсутствии однородности дисперсий с вероятностью α совершить ошибку.
Процедура сравнения заключается в том, что мы последовательно исключаем наибольшие дисперсии из рассмотрения в случае неоднородности, пока не находим хотя бы две однородные дисперсии или полное отсутствие таковых.
Первая итерация: G = S 2 max/∑Si 2 = 1,1792/(1,1792+0,0689+0,0989+0,0522) = 0,8428
Находим табличное значение Gα(f,n) = 0,5017, где n – число сравниваемых выборок (n=4), f = m-1 = 9– число степеней свободы, m – объём выборки (m=10), α=0,05 – уровень значимости.
Неравенство G>Gα(f,n) соблюдается, значит, мы отбрасываем гипотезу об однородности с вероятностью в 5% совершить ошибку.
Мы отбрасываем выборку с большей дисперсией 1,1792, и повторяем проверку для оставшихся трёх выборок.
G = S 2 max/∑Si 2 = 0,0989/(0,0689+0,0989+0,0522) = 0,4495
Находим табличное значение Gα(f,n) = 0,6167, где n – число сравниваемых выборок (n=3), f = m-1 = 9– число степеней свободы, m – объём выборки (m=10), α=0,05 – уровень значимости.
Неравенство G>Gα(f,n) нарушается, значит, мы принимаем гипотезу об однородности дисперсий трёх оставшихся выборок.
3) Оценка по критерию Бартлетта.
Преимуществом этого критерия является возможность сравнения выборок разного объёма. Мы используем выборки одинакового объёма, поэтому будем использовать упрощённые расчёты. С расчётами для выборок разного объёма можно ознакомиться в книге по ссылке ниже. Критерий Бартлетта чувствителен к отклонению распределения от нормального, поэтому при его применении необходимо осторожно подходить к выводам. При его применении лучше подтверждать выводы другими методами.
Критерий Бартлетта позволяет сравнивать большое число дисперсий, но мы всё же будем производить сравнение попарно большей и меньшей дисперсии аналогично F-критерию (в нашем случае это связано с тем, что так проще производить расчёты в Eхсel).
Гипотеза однородности принимается, если В/С 2 .
Т.к. выборки будут сравниваться попарно n=2.
Объём выборок одинаков m=m1=m2=10,
Степень свободы каждой выборки fj=m1-1=m2-1=10-1=9
Степень свободы для критерия Бартлетта f = ∑fj = f1+f2 = 9+9=18
| S 2 | 0,0522 | 0,0989 | 0,0689 | 1,1792 |
1) Вычисляем среднюю арифметическую сравниваемых дисперсий:
S 2 a = ∑S 2 i/n = (0,0522 + 1,1792)/2 = 0,615732
2) Вычисляем среднюю геометрическую сравниваемых дисперсий:
S 2 g = (∏Si 2 fj ) 1/ f = [(0,0522 2*9 )*(1,1792 2*9 )] 1/18 = 0,248161
3) Вычисляем критерий Бартлетта:
В = f*ln(S 2 a/S 2 g) = 18*ln(0,615732/0,248161) = 16,35721
4) Вычисляем коэффициент С:
С = 1 + (n+1)/(3*n*fj) = 1+(2+1)/(3*2*9) = 1,05555
5) Вычисляем отношение В к С:
В/С = 16,35721/1,05555 = 15,49630
Сравниваем полученное отношение В/С cтабличным значением хи-квадрат при числе степеней свободы ν=n-1=2-1 и уровне значимости 5%.
Рассчитанное значение больше критического, поэтому гипотеза однородности не может быть принята.
Мы отбрасываем самую большую дисперсию и продолжаем проверку однородности.
| S 2 | 0,0522 | 0,0989 | 0,0689 | — |
1) S 2 a = ∑S 2 i/n = (0,0522 + 0,0989)/2 = 0,07555
2) S 2 g = (∏Si 2 fj ) 1/ f = [(0,0522 2*9 )*(0,0989 2*9 )] 1/18 = 0,071855
3) В = f*ln(S 2 a/S 2 g) = 18*ln(0,07555/0,071855) = 0,901431
4) С = 1 + (n+1)/(3*n*fj) = 1+(2+1)/(3*2*9) = 1,05555
5) В/С = 0,901431/1,05555 = 0,85399
Сравниваем полученное отношение В/С cтабличным значением хи-квадрат при числе степеней ν=n-1=2-1=1 и уровне значимости 5%.
В/С=0,85399 2 = 3,841
Рассчитанное значение меньше критического, поэтому гипотеза однородности принимается.
Выводы: Данные анализа по критерию Фишера и критериям Кохрена и Бартлетта позволяют нам сделать вывод об однородности дисперсий выборок 1, 2 и 3 и неоднородности с ними выборки 4. Данные выборки 4 исключаются из дальнейшей проверки средних значений.
Относительно нашей основной задачи можно отметить, что для методики определения кобальта (выборка 4) либо строится своя индивидуальная контрольная карта, либо данные этой методики сравниваются с данными других методов (вынесенных за рамки нашего рассмотрения) для объединения их в одну группу. Для остальных методик будет проведена оценка однородности средних значений.
1. Агаянц И.М. Азы статистики в мире химии: Обработка экспериментальных данных – СПб: Научные основы и технологии, 2015. – 618 с.
Источник
