Дискретное множество
Дискре́тное простра́нство в общей топологии и смежных областях математики — это пространство, в котором все точки изолированы друг от друга в некотором смысле.
Содержание
Определения
- Пусть X есть некоторое множество, а
— семейство всех его подмножеств. Тогда
является топологией, называемой дискретной, а пара
называется дискре́тным топологи́ческим простра́нством.
- Пусть
— метрическое пространство, где метрика
определена следующим образом:
Тогда 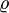
Замечание
Топология, индуцированная дискретной метрикой, является дискретной. Обратное, вообще говоря, неверно. Метрика, не являющаяся дискретной, может порождать дискретную топологию.
Примеры
- Пусть
где
, и
— дискретная метрика на X . Тогда
— дискретное метрическое, а следовательно и топологическое пространство.
- Пусть
и
Очевидно, заданная метрика не дискретна. Однако, она порождает дискретную топологию.
Свойства
- Топологическое пространство является дискретным тогда и только тогда, когда множество, содержащее лишь одну любую его точку, открыто.
- Множества, содержащие любую одну точку дискретного топологического пространства, являют собой базу дискретной топологии.
- Дискретное топологическое пространство компактно тогда и только тогда, когда оно конечно.
- Дискретное метрическое пространство ограничено.
- Любые два дискретных топологических пространства, имеющих одинаковую мощность, гомеоморфны.
- Любая функция, определённая на дискретном топологическом пространстве, непрерывна.
- Дискретное подмножество евклидова пространства не более чем счётно. Обратное, вообще говоря, неверно.
См. также
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Дискретное множество» в других словарях:
дискретное множество — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN discrete set … Справочник технического переводчика
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Дискретное логарифмирование — (DLOG) задача обращения функции в некоторой конечной мультипликативной группе . Наиболее часто задачу дискретного логарифмирования рассматривают в мультипликативной группе кольца вычетов или конечного поля, а также в группе точек эллиптической… … Википедия
Дискретное пространство — в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры … Википедия
Дискретное метрическое пространство — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Дискретное топологическое пространство — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ — область математики, занимающаяся исследованием и решением экстремальных задач на конечных множествах. Пусть М=<а 1, а 2, . а п>и f числовая функция, определенная на элементах множества М. Требуется найти элемент на к ром достигается абсолютный … Математическая энциклопедия
Массивное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Несвязное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Источник
Основы дискретной математики
Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.
Об этой статье
Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!
ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?
Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.
Мы рассмотрим пять основных разделов в следующем порядке.
ЛОГИКА
Что такое логика?
Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.
Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).
Начнем с азов. Рассмотрим следующее высказывание на естественном языке:
«Если я голоден, я ем».
Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:
A => B (то есть из A следует B)
NB. Посылка и следствие являются суждениями.
Логические выражения
Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.
Например, 10 4 — ИСТИНА.
Логические операции
Суждение P — это утверждение, которое может быть как истинным, так и ложным.
Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).
Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).
Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.
Источник
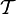 — семейство всех его подмножеств. Тогда
— семейство всех его подмножеств. Тогда 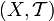 называется дискре́тным топологи́ческим простра́нством.
называется дискре́тным топологи́ческим простра́нством.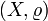 — метрическое пространство, где метрика
— метрическое пространство, где метрика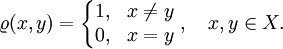
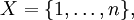 где
где 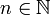 , и
, и 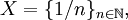 и
и 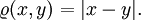 Очевидно, заданная метрика не дискретна. Однако, она порождает дискретную топологию.
Очевидно, заданная метрика не дискретна. Однако, она порождает дискретную топологию.

