Что значит диаметрально противоположные точки круговой трассы
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 42 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 28 км/ч больше скорости другого?
Это задание ещё не решено, приводим решение прототипа.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 21 км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому
Таким образом, мотоциклисты поравняются через часа или через 20 минут.
Приведём другое решение.
Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.
Источник
II.Задачи на движение по окружности
Решение задач на движение по окружности в одном направлении точно такое же, как решение задач на движение в одном направлении по прямой. Если два объекта одновременно начинают движение по окружности из одной точки в одну сторону со скоростями v1 и v2 соответственно (v1 > v2), то первый объект приближается ко второму со скоростью v1 — v2 и в момент, когда первый объект в первый раз догоняет второй, он проходит расстояние на один круг больше. И мы имеем дело с формулой, которая ничем не отличается от формулы, полученной для задач на движение вдогонку:
S – длина окружности;
t – время, через которое первый объект в первый раз догоняет второй объект.
Задача 1: «Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч».
Так как первый автомобиль через 40 минут после старта опережал второй на один круг, то это значит, что через 40 минут первый автомобиль догнал второй в первый раз. Значит:
1) 40 мин = 
2) 14 : 
3) 80 – 21 = 59 (км/ч) – скорость второго автомобиля.
Задача 2: «Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?»
В этом случае мотоциклисты начинают движение из разных точек окружности. Так как это диаметрально противоположные точки, то первоначальное расстояние между мотоциклистами рано 7 км. Так как скорость одного из них на 21 км/ч больше скорости другого, то скорость сближения равна 21 км/ч. Значит:
1) 7 : 21 = 
2) 
Задача 3: «Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?»
Скорость движения минутной стрелки 12 делений/час, а часовой – 1 деление/час (под делением подразумевается расстояние между двумя соседними цифрами на циферблате часов). Так как часы со стрелками показывают 8 часов 00 минут, то первоначальное расстояние между стрелками составляет 8 делений. После того, как минутная стрелка поравняется с часовой в первый раз, она должна будет догнать часовую стрелку еще три раза, то есть обогнать ее на три круга.
1) 12 -1 = 11 (делений/час) – скорость сближения стрелок;
2) 8 : 11 = 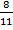
3) 12 * 3 = 36 (делений) – длина трех кругов;
4) 36 : 11 = 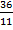
5) 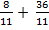
6)
1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 30 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 18 км/ч больше скорости другого? (50)
2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 78 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. (63)
3. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. (80)
4. Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой? (540)
5. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч. (108)
Источник
Что значит диаметрально противоположные точки круговой трассы
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 21 км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому
Таким образом, мотоциклисты поравняются через часа или через 20 минут.
Приведём другое решение.
Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Пусть скорость второго автомобиля равна км/ч. За 2/3 часа первый автомобиль прошел на 14 км больше, чем второй, отсюда имеем
Добрый день, на мой взгляд, гораздо проще сменить систему отсчёта( Найдём скорость удаления(21) и (80-21=59).
Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
К моменту первого обгона мотоциклист за 10 минут проехал столько же, сколько велосипедист за 40 минут, следовательно, его скорость в 4 раза больше. Поэтому, если скорость велосипедиста принять за x км/час, то скорость мотоциклиста будет равна 4x, а скорость их сближения — 3x км/час.
C другой стороны, второй раз мотоциклист догнал велосипедиста за 30 минут, за это время он проехал на 30 км больше. Следовательно, скорость их сближения составлят 60 км/час.
Итак, 3х = 60 км/час, откуда скорость велосипедиста равна 20 км/час, а скорость мотоциклиста равна 80 км/час.
Вы утверждаете что второй раз мотоциклист догнал велосипедиста за 30 минут и за это время он проехал на 30 км больше. Следовательно, скорость их сближения составлят 60 км/час, но это означает, что велосипедист остановился в той точке, где мотоциклист догнал его первый раз, и оставался в ней неподвижно, пока мотоциклист проезжал круг и возвращался в эту точку. Но на самом-то деле велосипедист двигался 30 мин, пока мотоциклист проезжал круг. Значит, чтобы мотоциклист догнал велосипедиста мотоциклисту нужно проехать 30 км + расстояние, которое прошел велосипедист, пока двигался мотоциклист.
Вы правы в том, что они двигались одновременно и второй раз встретились в другой точке. Это не противоречит сказанному в решении: при этом мотоциклист проехал на 30 км больше.
Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
До четвертой встречи стрелок минутная должна сначала пройти 8 разделяющих их часовых делений (поскольку часы показывают 8 часов), затем 3 раза обойти полный круг, то есть пройти 36 часовых делений, и пройти последние L делений, на которые поворачивается часовая стрелка за время движения минутной. Скорость движения минутной стрелки в 12 раз больше часовой: пока часовая обходит один полный круг, минутная проходит 12 кругов. Приравняем время движения часовой и минутной стрелок до их четвертой встречи:
Часовая стрелка пройдет 4 деления, что соответствует 4 часам, то есть 240 минутам.
Приведем арифметическое решение.
Скорость минутной стрелки 1 круг в час, а часовой — круга в час, поэтому скорость удаления или сближения стрелок равна
круга в час. Расстояние между стрелками, отсчитываемое по окружности, в начальный момент составляет 40 минут или
круга. С момента первой встречи до момента четвёртой встречи минутная стрелка должна опередить часовую на три круга. Всего
круга. Поэтому необходимое время равно
часа или 240 минут.
Приведем другое решение.
Ясно, что в первый раз стрелки встретятся между 8 и 9 часами, второй раз — между 9 и 10 часами, третий — между 10 и 11, четвертый — между 11 и 12 часами, то есть ровно в 12 часов. Таким образом, они встретятся ровно через 4 часа, что составляет 240 минут.
Помещаем решение в общем виде.
Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30h + 0,5m градусов, а минутная — на 6m градусов относительно 12-часового деления.
Пусть в первый раз стрелки встретятся через t1 минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6m + 6t1 = 30h + 0,5m + 0,5t1, т. е. t1 = (60h − 11m)/11 (*). В противоположном случае получаем уравнение 6m + 6t1 = 30h + 0,5m + 0,5t1 + 360, откуда t1 = (60h − 11m + 720)/11 (**).
Пусть во второй раз стрелки встретятся через t2 минут после первого, тогда 0,5t2 = 6t2 − 360, откуда t2 = 720/11 (***). Это же верно для каждого следующего оборота.
Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: tn = (60h − 11m + 720(n − 1))/11 или tn = (60h − 11m + 720n − 720)/11.
Источник
Портал для школьника. Самоподготовка
На одной точке круговой трассы. Задачи на круговое движение
Тогда если \(l\) — длина круга, \(t_1\) — время, через которое они окажутся в одной точке в первый раз, то:
То есть за \(t_1\) первое тело пройдет расстояние на \(l\) большее, чем второе тело.
Если \(t_n\) — время, через которое они в \(n\) –ый раз окажутся в одной точке, то справедлива формула: \[<\large
\(\blacktriangleright\) Пусть два тела начали движение из разных точек в одном направлении со скоростями \(v_1>v_2\) .
Тогда задача легко сводится к предыдущему случаю: нужно найти сначала время \(t_1\) , через которое они окажутся в одной точке в первый раз.
Если на момент начала движения расстояние между ними \(\buildrel\smile\over
Уровень задания: Легче ЕГЭ
Два спортсмена стартуют в одном направлении из диаметрально противоположных точек круговой дорожки. Они бегут с разными непостоянными скоростями. Известно, что в тот момент, когда спортсмены впервые поравнялись, они прекратили тренировку. На сколько кругов больше пробежал спортсмен с большей средней скоростью, чем другой спортсмен?
Назовём спортсмена с большей средней скоростью первым. Сначала первому спортсмену нужно было пробежать полкруга, чтобы достичь места старта второго спортсмена. После этого ему предстояло пробежать столько же, сколько пробежал второй спортсмен (грубо говоря, после того, как первый спортсмен пробежал полкруга, ему до встречи надо было пробежать каждый метр дорожки, который пробежал второй спортсмен, причём столько же раз, сколько этот метр пробежал второй).
Таким образом, первый спортсмен пробежал на \(0,5\) круга больше.
Уровень задания: Легче ЕГЭ
Кот Мурзик бегает от пса Шарика по кругу. Скорости Мурзика и Шарика постоянны. Известно, что Мурзик бежит в \(1,5\) раза быстрее Шарика и за \(10\) минут они в сумме пробегают два круга. За сколько минут Шарик пробежит один круг?
Так как Мурзик бежит в \(1,5\) раза быстрее Шарика, то за \(10\) минут Мурзик и Шарик в сумме пробегают такое же расстояние, которое пробежал бы Шарик за \(10\cdot (1 + 1,5) = 25\) минут. Следовательно, Шарик пробегает два круга за \(25\) минут, тогда один круг Шарик пробегает за \(12,5\) минут
Уровень задания: Равен ЕГЭ
Из точки A круговой орбиты далёкой планеты одновременно в одном направлении вылетели два метеорита. Скорость первого метеорита на 10000 км/ч больше, чем скорость второго. Известно, что впервые после вылета они встретились через 8 часов. Найдите длину орбиты в километрах.
В тот момент, когда они впервые встретились, разница расстояний, которые они пролетели, равна длине орбиты.
За 8 часов разница стала \(8 \cdot 10000 = 80000\) км.
Уровень задания: Равен ЕГЭ
Вор, укравший сумочку, убегает от хозяйки сумочки по круговой дороге. Скорость вора на 0,5 км/ч больше, чем скорость хозяйки сумочки, которая бегает за ним. Через сколько часов вор догонит хозяйку сумочки во второй раз, если длина дороги, по которой они бегают, равна 300 метрам (считайте, что в первый раз он её догнал уже после кражи сумочки)?
Вор догонит хозяйку сумочки во второй раз в тот момент, когда расстояние, которое он пробежит, станет на 600 метров больше, чем расстояние, которое пробежит хозяйка сумочки (с момента кражи).
Так как его скорость на \(0,5\) км/ч больше, то за час он пробегает на 500 метров больше, тогда за \(1: 5 = 0,2\) часа он пробегает на \(500: 5 = 100\) метров больше. На 600 метров больше он пробежит за \(1 + 0,2 = 1,2\) часа.
Пусть \(v\) км/ч – скорость хозяйки сумочки, тогда
\(v + 0,5\) км/ч – скорость вора.
Пусть \(t\) ч – время, через которое вор догонит хозяйку сумочки во второй раз, тогда
\(v\cdot t\) – расстояние, которое пробежит хозяйка сумочки за \(t\) ч,
\((v + 0,5)\cdot t\) – расстояние, которое пробежит вор за \(t\) ч.
Вор догонит хозяйку сумочки во второй раз в тот момент, когда пробежит ровно на 2 круга больше неё (то есть на \(600\) м = \(0,6\) км), тогда \[(v + 0,5)\cdot t — v\cdot t = 0,6\qquad\Leftrightarrow\qquad 0,5\cdot t = 0,6,\] откуда \(t = 1,2\) ч.
Уровень задания: Равен ЕГЭ
Два мотоциклиста стартуют одновременно из одной точки круговой трассы в разных направлениях. Скорость первого мотоциклиста в два раза больше, чем скорость второго. Через час после старта они встретились в третий раз (считайте, что в первый раз они встретились уже после старта). Найдите скорость первого мотоциклиста, если длина трассы 40 км. Ответ дайте в км/ч.
В тот момент, когда мотоциклисты встретились в третий раз, суммарное расстояние, которое они проехали, было \(3 \cdot 40 = 120\) км.
Так как скорость первого в 2 раза больше, чем скорость второго, то он проехал из 120 км часть в 2 раза большую, чем второй, то есть 80 км.
Так как встретились в третий раз они через час, то 80 км первый проехал за час. Его скорость 80 км/ч.
Уровень задания: Равен ЕГЭ
Два бегуна стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой дорожки, длина которой 400 метров. Через сколько минут бегуны поравняются в первый раз, если первый бегун за час пробегает на 1 километр больше, чем второй?
За час первый бегун пробегает на 1000 метров больше, чем второй, значит на 100 метров больше он пробежит за \(60: 10 = 6\) минут.
Изначальное расстояние между бегунами равно 200 метров. Они поравняются, когда первый бегун пробежит на 200 метров больше, чем второй.
Это произойдёт через \(2 \cdot 6 = 12\) минут.
Уровень задания: Равен ЕГЭ
Из города M по круговой дороге длиной 220 километров вышел турист, а через 55 минут следом за ним из города M отправился автомобилист. Через 5 минут после отправления он догнал туриста в первый раз, а еще через 4 часа после этого догнал его во второй раз. Найдите скорость туриста. Ответ дайте в км/ч.
После первой встречи автомобилист догнал туриста (во второй раз) через 4 часа. К моменту второй встречи автомобилист проехал на круг больше, чем прошёл турист (то есть на \(220\) км).
Так как за эти 4 часа автомобилист обогнал туриста на \(220\) км, то скорость автомобилиста на \(220: 4 = 55\) км/ч больше, чем скорость туриста.
Пусть теперь скорость туриста \(v\) км/ч, тогда до первой встречи он успел пройти \ автомобилист успел проехать \[(v + 55)\dfrac<5> <60>= \dfrac
Пусть \(v\) км/ч – скорость туриста.
Пусть \(w\) км/ч – скорость автомобилиста. Так как \(55\) минут \(+ 5\) минут \(= 1\) час, то
\(v\cdot 1\) км – расстояние, которое прошёл турист до первой встречи. Так как \(5\) минут \(= \dfrac<1><12>\) часа, то
\(w\cdot \dfrac<1><12>\) км – расстояние, которое проехал автомобилист до первой встречи. Расстояния, которые они проехали до первой встречи, равны: \ За следующие 4 часа автомобилист проехал больше, чем прошёл турист на круг (на \(220\) \ \
При использовании в упражнении величин, которые связаны с расстоянием (скорость, длина круга), решить их можно путем сведения к перемещению по прямой.
Наибольшую сложность у школьников Москвы и других городов, как показывает практика, вызывают задачи на круговое движение в ЕГЭ, поиск ответа в которых связан с применением угла. Для решения упражнения длину окружности можно задать как часть круга.
Повторить эти и другие алгебраические формулы вы можете в разделе «Теоретическая справка». Для того чтобы научиться применять их на практике, прорешайте упражнения по данной теме в «Каталоге».
Задачи на движение по круговой трассе. Задачи на движение по круговой трассе.
1.
2.
3.
4.
5.
6.
Вариант 1.
которой равна 14 км. Через сколько минут мотоциклисты поравняются
в первый раз, если скорость одного из них на 21 км/ч больше скорости
другого?
Из одной точки круговой трассы, длина которой равна 14 км,
Скорость первого автомобиля равна 80 км/ч, и через 40 минут после
скорость
Из пункта A круговой трассы выехал велосипедист. Через 30 минут он
еще не вернулся в пункт А и из пункта А следом за ним отправился
мотоциклист. Через 10 минут после отправления он догнал
велосипедиста в первый раз, а еще через 30 минут после этого догнал
его во второй раз. Найдите скорость мотоциклиста, если длина трассы
равна 30 км. Ответ дайте в км/ч.
Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по
кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали
одновременно, а на финиш первый пришёл раньше второго на 10 минут.
первый гонщик в первый раз обогнал второго на круг через 15 минут?
Ответ дайте в км/ч.
один час, когда одному из них оставалось 1 км до окончания первого
круга, ему сообщили, что второй бегун прошёл первый круг 20 минут
км/ч меньше скорости второго.
трассы в метрах, если второе тело возвращается в точку А через 36
минут после встречи.
1.
2.
3.
4.
5.
6.
Вариант 2.
Два мотоциклиста стартуют одновременно в одном направлении из
двух диаметрально противоположных точек круговой трассы, длина
которой равна 16 км. Через сколько минут мотоциклисты
поравняются в первый раз, если скорость одного из них на 10 км/ч
больше скорости другого?
одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 101 км/ч, и через 20 минут после
старта он опережал второй автомобиль на один круг. Найдите
Из пункта A круговой трассы выехал велосипедист, а через 50 минут
следом за ним отправился мотоциклист. Через 5 минут после отправ
ления он догнал велосипедиста в первый раз, а еще через 30 минут
после этого догнал его во второй раз. Найдите скорость
мотоциклиста, если длина трассы равна 50 км. Ответ дайте в км/ч.
Два гонщика участвуют в гонках. Им предстоит проехать 68 кругов по
кольцевой трассе протяжённостью 6 км. Оба гонщика стартовали
одновременно, а на финиш первый пришёл раньше второго на
15 минут. Чему равнялась средняя скорость второго гонщика, если
известно, что первый гонщик в первый раз обогнал второго на круг
через 60 минут? Ответ дайте в км/ч.
Два бегуна одновременно стартовали в одном направлении из одного и
того же места круговой трассы в беге на несколько кругов. Спустя
один час, когда одному из них оставалось 3 км до окончания первого
назад. Найдите скорость первого бегуна, если известно, что она на
5км/ч меньше скорости второго.
Из точки А круговой трассы одновременно начинают равномерное
трассы в метрах, если второе тело возвращается в точку А через 20
минут после встречи.
1.
2.
3.
4.
5.
6.
Вариант 3.
Два мотоциклиста стартуют одновременно в одном направлении из
двух диаметрально противоположных точек круговой трассы, длина
которой равна 20 км. Через сколько минут мотоциклисты поравняются
в первый раз, если скорость одного из них на 15 км/ч больше скорости
другого?
Из одной точки круговой трассы, длина которой равна 8 км,
одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 114 км/ч, и через 20 минут после
второго автомобиля. Ответ дайте в км/ч.
следом за ним отправился мотоциклист. Через 8 минут после
отправления он догнал велосипедиста в первый раз, а еще через 21
минуту после этого догнал его во второй раз. Найдите скорость
мотоциклиста, если длина трассы равна 35 км. Ответ дайте в км/ч.
Два гонщика участвуют в гонках. Им предстоит проехать 94 круга по
кольцевой трассе протяжённостью 7,5 км. Оба гонщика стартовали
одновременно, а на финиш первый пришёл раньше второго на 18 минут.
Чему равнялась средняя скорость второго гонщика, если известно, что
первый гонщик в первый раз обогнал второго на круг через 50 минут?
Ответ дайте в км/ч.
Два бегуна одновременно стартовали в одном направлении из одного и
того же места круговой трассы в беге на несколько кругов. Спустя
один час, когда одному из них оставалось 4 км до окончания первого
круга, ему сообщили, что второй бегун прошёл первый круг 6 минут
назад. Найдите скорость первого бегуна, если известно, что она на 6
км/ч меньше скорости второго.
Из точки А круговой трассы одновременно начинают равномерное
движение в противоположных направлениях два тела. Первое тело к
моменту их встречи проходит на 300 метров больше, чем второе, и
возвращается в точку А через 5 минут после встречи. Найдите длину
1.
2.
3.
4.
5.
6.
Вариант 4.
Два мотоциклиста стартуют одновременно в одном направлении из
двух диаметрально противоположных точек круговой трассы, длина
которой равна 40 км. Через сколько минут мотоциклисты
поравняются в первый раз, если скорость одного из них на 25 км/ч
больше скорости другого?
Из одной точки круговой трассы, длина которой равна 12 км,
одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 106 км/ч, и через 48 минут после
старта он опережал второй автомобиль на один круг. Найдите
скорость второго автомобиля. Ответ дайте в км/ч.
Из пункта A круговой трассы выехал велосипедист, а через 40 минут
следом за ним отправился мотоциклист. Через 10 минут после
отправления он догнал велосипедиста в первый раз, а еще через 36
минут после этого догнал его во второй раз. Найдите скорость
мотоциклиста, если длина трассы равна 36 км. Ответ дайте в км/ч.
Двум гонщикам предстоит проехать 85 кругов по кольцевой трассе
протяжённостью 8 км. Оба гонщика стартовали одновременно, а на
финиш первый пришёл раньше второго на 17 минут. Чему равнялась
средняя скорость второго гонщика, если известно, что первый гонщик
в первый раз обогнал второго на круг через 48 минут? Ответ дайте в
км/ч.
Два бегуна одновременно стартовали в одном направлении из одного и
того же места круговой трассы в беге на несколько кругов. Спустя
один час, когда одному из них оставалось 7 км до окончания первого
круга, ему сообщили, что второй бегун пробежал первый круг 3 минут
назад. Найдите скорость первого бегуна, если известно, что она на 8
км/ч меньше скорости второго.
Из точки А круговой трассы одновременно начинают равномерное
движение в противоположных направлениях два тела. К моменту их
встречи первое тело проходит на 200 м больше, чем второе, и
возвращается в точку А через 25 мин после встречи. Найдите длину
Шинкарев Егор Александрович
Нестандартные задачи на движение
Научный руководитель проекта Кудрявцева Наталья Николаевна
В сборнике приведены подробные решения задач, условно отнесенных к следующим группам: на круговое движение, на движение протяжённых тел и предложены задачи для самостоятельного решения. Данную подборку задач можно использовать для отработки навыков решения задач данного типа при подготовке к ЕГЭ и олимпиадам по математике. Сборник может быть полезен для учащихся 8-11 классов, учителям для организации закрепления и повторения задач на движение как на уроке, так и внеклассных занятиях.
Глава 1. Задачи на движение по кругу
§ 1.1. Задачи на движение по кругу, в одном направлении, в одно время из одной точки____________________________________________________4
§ 1.2. Задачи на движение по кругу, в одном направлении, в одно время из диаметрально противоположных точек_____________________________6
§ 1.3. Задачи на движение по кругу, в одном направлении, в разное время из одной точки.………….7
§ 1.4. Задачи на движение по кругу, в противоположных направлениях, в одно время из одной точки.………………..8
Глава 2. Задачи на движение протяжённых тел
§ 2.1. Задачи на движение двух протяжённых тел в одну сторону
§ 2.2. Задачи на движение двух протяженных тел навстречу
§ 2.3. Задачи на движение одного протяжённого тела относительно другого неподвижного
§ 2.4. Задачи на движение протяжённого тела относительно неподвижной точки
§ 2.5. Задачи на движение протяжённого тела и точки навстречу
§ 2.6 задачи на движение протяжённого тела и точки в одну сторону______
В практике встречается очень много интересных задач на движение. Занимательные задачи предлагают на различных олимпиадах и на выпускных экзаменах. В данном сборнике собраны только задачи, условно отнесенные к следующим группам: задачи на движение по кругу, задачи на движение протяжённых тел.
В каждой группе выделены подгруппы, отличающиеся друг от друга способами решения.
В данном сборнике задач представлены подборки задач каждого типа с ответами. В сборнике приведены подробные решения задач каждого типа и предложены задачи для самостоятельного решения. Данную подборку задач можно использовать для отработки навыков решения задач данного типа при подготовке к ОГЭ, ЕГЭ и олимпиадам по математике. Сборник может быть полезен для учащихся 8-11 классов, учителям для организации закрепления и повторения задач на движение, как на уроке, так и внеклассных занятиях.
Задачи на движение по кругу
§1.1 Задачи на движение по кругу, в одном направлении, в одно время из одной точки
Задача: Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Зная, что за 2/3 часа первый автомобиль прошел на круг, то есть на 14 км больше, чем второй, составим уравнение.
1. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.(13)( )
2. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч. (108) ( )
3. Двум гонщикам предстоит проехать 85 кругов по кольцевой трассе протяжённостью 8 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 17 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 48 минут? Ответ дайте в км/ч.
4. Двум гонщикам предстоит проехать 68 кругов по кольцевой трассе протяжённостью 6 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 15 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 60 минут? Ответ дайте в км/ч.
5. Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка?(1/80 и 1/90 части окружности)( )
§1.2. Задачи на движение по кругу, в одном направлении, в одно время из диаметрально противоположных точек
Задача: Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Пусть мотоциклисты находятся в пути одно и то же время, равное t
часов. Для того чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы, то есть 14:2=7 км. Поэтому путь, пройденный вторым мотоциклистом, на 7 км больше, чем путь, пройденный первым:
Таким образом, мотоциклисты поравняются через t= часа или через 20 минут.
Приведём другое решение
Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.
Задачи для самостоятельного решения:
6. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 22 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости другого?(33)(https://www.metod-kopilka.ru/konspekt_uroka_matematiki_po_teme_reshenie_zadach_na_dvizhenie_po_okruzhnosti-59657.htm)
7. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 5 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 5 км/ч больше скорости другого? (30) (https://www.metodkopilka.ru/konspekt_uroka_matematiki_po_teme_reshenie_zadach_na_dvizhenie_po_okruzhnosti-59657.htm)
8 . Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? (20)
9 . Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 27 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 27 км/ч больше скорости другого? (30)
10. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 6 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 9 км/ч больше скорости другого? (20)
§1.3. Задачи на движение по кругу, в одном направлении, в разное время из одной точки
Задача: Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
К моменту первого обгона мотоциклист за 10 минут проехал столько же, сколько велосипедист за 40 минут, следовательно, его скорость в 4 раза больше. Поэтому, если скорость велосипедиста принять за x км/час, то скорость мотоциклиста будет равна 4x км/ч, а скорость их сближения — 3x км/час.
C другой стороны, второй раз мотоциклист догнал велосипедиста за 30 минут, за это время он проехал на 30 км больше. Следовательно, скорость их сближения составляет 60 км/час.
Итак, 3х=60 км/час, откуда скорость велосипедиста равна 20 км/час, а скорость мотоциклиста равна 80 км/час.
Задачи для самостоятельного решения:
11 . Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч. (6) ( https://www.metodkopilka.ru/konspekt_uroka_matematiki_po_teme_reshenie_zadach_na_dvizhenie_po_okruzhnosti-59657.htm
12. Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. (60) ( https://www.metodkopilka.ru/konspekt_uroka_matematiki_po_teme_reshenie_zadach_na_dvizhenie_po_okruzhnosti-59657.htm)
13. Из пункта “А” круговой трассы выехал велосипедист, а через 50 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 18 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 15 км. Ответ дайте в км/ч. (60)
14. Из пункта “А” круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 8 мин после отправления он догнал велосипедиста в первый раз, а еще через 12 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 15 км. Ответ дайте в км/ч.(95)
15. Из пункта “А” круговой трассы выехал велосипедист, а через 40 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 36 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 36 км. Ответ дайте в км/ч. (75)
§1.4. Задачи на движение по кругу, в противоположных направлениях, в одно время из одной точки
З ад ача 1: На окружности взята некоторая точка А. Из этой точки одновременно выходят два тела, которые движутся по данной окружности равномерно в противоположных направлениях. В момент их встречи оказалось, что первое тело прошло на 10 метров больше второго. Кроме того, первое тело пришло в точку А через 9 секунд, а второе – через 16 секунд после встречи. Определить длину окружности в метрах.
Пусть х – скорость одной точки, движущейся по часовой стрелке, а у– скорость второй. Тогда до встречи первая точка пройдет расстояние xt, а вторая пройдет yt расстояние.
После встречи первой точке до места старта нужно пройти такое расстояние, какое вторая прошла до встречи, и тратит первая точка на это время, равное 10 с, а второй наоборот, нужно пройти то расстояние, которое прошла до встречи первая, и тратит она на это 16 с. Получим такие равенства:
Выразим время движения точек до встречи t
По условию, первое тело прошло на 10 м больше второго, то есть
Заменяем в этом уравнении одну из неизвестных:
И находим Y=2,5 откуда x= .
Полная длина круга равна: 70
Ответ: длина окружности 70 м.
Задачи для самостоятельного решения:
16. Два тела, движущиеся в разные стороны по окружности длиной 500м с постоянными скоростями, встречаются каждые 125сек. При движении в одну сторону первое тело догоняет второе каждые 12,5 сек. Найдите скорости каждого тела. (22 и 18)
17. Из точки А круговой трассы одновременно начинают равномерное движение в противоположных направлениях два тела. Первое тело к моменту их встречи проходит на 100 метров больше, чем второе, и возвращается в точку А через 9 минут после встречи. Найдите длину трассы в метрах, если второе тело возвращается в точку А через 16 минут после встречи. (700)
18. Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях — через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности?(1120 м; 40 м/мин, 30 м/мин)
Задачи на движение протяжённых тел
§2.1. Задачи на движение двух протяжённых тел в одну сторону
Задача: По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 130 метров, второй- длиной 120 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 600 метров. Через 11 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 800 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?(http://www.ug.ru/method_article/519)
600+130+120+800= 1650 м
Расстояние, пройденное носом 2 сухогруза равно: первоначальное расстояние от носа 2 сухогруза до кормы 1(600) + длина 1(130) + длина 2(120) + конечное расстояние от носа 1 до кормы 2(800) = 1650 м
V = 1650: 11= 150 м/мин =9 км/ч
Задачи для самостоятельного решения:
21. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 2 минутам. Ответ дайте в метрах. (200)
22. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 70 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 200 метров. Через 8 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 500 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? (6.6)
23. По морю параллельными курсами в одном направлении следуют две баржи: первая длиной 70 метров, вторая — длиной 30 метров. Сначала вторая баржа отстает от первой, и в некоторый момент времени расстояние от кормы первой баржи до носа второй составляет 250 метров. Через 14 минут после этого уже первая баржа отстает от второй так, что расстояние от кормы второй баржи до носа первой равно 350 метрам. На сколько километров в час скорость первой баржи меньше скорости второй? (3)
24. По морю параллельными курсами в одном направлении следуют две баржи: первая длиной 60 метров, вторая- длиной 40 метров. Сначала вторая баржа отстает от первой, и в некоторый момент времени расстояние от кормы первой баржи до носа второй составляет 200 метров. Через 18 минут после этого уже первая баржа отстает от второй так, что расстояние от кормы второй баржи до носа первой равно 300 метрам. На сколько километров в час скорость первой баржи меньше скорости второй? (2.1)
25 . По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? (6)
Задачи на цифровую запись числа
Задача 1: Найдите наименьшее четырёхзначное число, кратное 11, у которого произведение его цифр равно 12.
Число должно быть кратно 11, то есть разность цифр, стоящих на чётных позициях и цифр, стоящих на нечётных позициях кратно 11, рассмотрим случай, когда их разность равна 0. Заметим, что 0 не должен встречаться, так как при умножении на 0 получим 0. Так как число наименьшее возьмём первую цифру 1. Число примет вид 1bcd. И так 1 + c = b + d и c×b×d=12. При этом если представить 12 в виде произведения 3-х чисел, то получим 12= 2×3×2, при этом 2+2 = 3+1 и получаем 1232
Задачи для самостоятельного решения:
26. Найдите четырёхзначное число, кратное 22, произведение цифр которого равно 40. В ответе укажите какое-нибудь одно такое число.
27. Найдите четырёхзначное число, кратное 22, произведение цифр которого равно 60. В ответе укажите какое-нибудь одно такое число.
28. Найдите четырёхзначное число, кратное 18, произведение цифр которого равно 24. В ответе укажите какое-нибудь одно такое число.
29. Найдите четырёхзначное число кратное 33, произведение цифр которого равно 40. В ответе укажите какое-нибудь одно такое число.
30. Найдите наименьшее четырёхзначное число, кратное 11, у которого произведение его цифр равно 12
Задача 2: Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 0 и делится на 24.
Чтобы число делилось на 24 оно должно делится на 3 и на 8.
Число делится на 8, если три его последние цифры образуют число, делящееся на 8.
Искомое число записывается только нулями и единицами, значит, оно заканчивается на 000.Число делится на 3, если его сумма цифр числа делится на 3. Поскольку три последние цифры числа нули, первые три должны быть единицами. Таким образом, единственное число, удовлетворяющее условию задачи, это число 111 000.
Ответ: 111000
Задачи для самостоятельного решения:
31. Найдите шестизначное натуральное число, которое записывается только цифрами 2 и 0 и делится на 120. В ответе укажите какое-нибудь одно такое число.
32. Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 5 и делится на 45. В ответе укажите какое-нибудь одно такое число.
33. Найдите шестизначное натуральное число, которое записывается только цифрами 2 и 3 и делится на 6.
34. Найдите шестизначное натуральное число, которое записывается только цифрами 7 и 3 и делится на 11.
35. Найдите шестизначное натуральное число, которое записывается только цифрами 3, 4, 9 и 5 и делится на 9.
36. Найти наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.
37. Найдите шестизначное натуральное число, делящееся на 47, которое записывается только цифрами 2, 8, и 0.
Задача 3: Сумма цифр трёхзначного натурального числа А делится на 12. Сумма цифр числа А+6 также делится на 12 найдите Наименьшее возможное число А.
Решение: Для удобства назовем наше число abc. Каждая буква обозначает отдельный разряд числа A: a — сотни, b — десятки, c — единицы. Сумма цифр a + b + c должна делиться нацело на 12. Предположим, что так оно и есть, и попробуем подобрать такое число A + 6, чтобы сумма его цифр также делилась на 12. Заметим, что сумма цифр числа A + 6 должна отличаться от суммы цифр числа A на 12, 24, . Иначе она не будет делиться на 12. Рассмотрим все возможные варианты:
Вариант 1. Если c
38. Сумма цифр натурального трёхзначного числа А делится на 13. Сумма цифр числа А+5 также делится на 13. Найдите такое число А.
39. Сумма цифр натурального трёхзначного числа А делится на 12. Сумма цифр числа А+6 также делится на 12. Найдите наименьшее число А, удовлетворяющее условию А › 700.
40. Найдите трёхзначное число А, обладающие всеми следующими свойствами:
сумма цифр числа А делится на 6
сумма цифр числа А+3 также делится на 6
число А больше 350 и меньше 400
В ответе укажите какое-нибудь одно такое число.
Задачи на вычёркивание и дописывание чисел
Задача 1: Вычеркните в числе 123456 три цифры так, чтобы получившееся число делилось на 27. В ответе укажите число.
Начнем с чисел, которые начинаются с цифры 1, что бы порядок не был нарушен:
123, 124, 125, 126, 134, 135, 136, 145, 146, 156.
Среди этих чисел 135 делится на 27 (13–8·5= –27)
Далее проверяем числа, которые начинаются с цифры 2:
234, 235, 236, 245, 246, 256
Проверяем числа, которые начинаются с 3:
345, 346, 356.
Ни одно число не делится на 27.
Переходим к числам которые начинаются на цифру 4.
456: не делится на 27.
Таким образом, получаем число 135
Задачи для самостоятельного решения:
41. Вычеркните в числе 123456 три цифры так, чтобы получившееся число делилось на 35. В ответе укажите число.
42. Вычеркните в числе 123456 три цифры так, чтобы получившееся число делилось на 5. В ответе укажите число.
43. Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите ровно одно получившееся число.
44. Вычеркните в числе 141565041 три цифры так, чтобы получившееся число делилось на 30. В ответе укажите ровно одно получившееся число.
45. Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Задача 2: К числу 26 допиши левее и правее по цифре, чтоб полученное число было кратным 45.
Сумма цифр этого числа должна делиться на 9, само число должно делиться на 5., значит последняя цифра 0 или 5. а дальше подбираем первую цифру.
Ответ: 1260 или 5262
Задачи для самостоятельного решения:
46. К числу 374 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 45.
47. Приписать к 1022 слева и справа по одной цифре так чтобы полученное шестизначное число делилось на 7, 8, 9.
48. К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.
49. К числу 10 припишите слева и справа по одной цифре, чтобы получилось число, кратное 72.
50. К числу 2012 припишите справа две цифры так, чтобы полученное шестизначное число делилось на 36.
Ответы на задачи:
Список используемой литературы:
1) Школьные знания — портал [Электронный ресурс]. — Режим доступа: https://znanija.com/task/, свободный. — Заглавие с экрана.
2) mail . ru — портал [Электронный ресурс]. — Режим доступа: https://otvet.mail.ru/question/, свободный. — Заглавие с экрана.
3) ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни / И. В. Ященко, И. Р. Высоцкий, А. В. Забелин, П. И. Захаров, С. Л. Крупецкий, В. Б. Некрасов, М. А. Посицельская, С. Е. Посицельский, Е. А. Семенко, А. В. Семёнов, В. А. Смирнов, Н. А. Сопрунова, А. В. Хачатурян, И. А. Хованская, С. А. Шестаков, Д. Э. Шноль; под ред. И. В. Ященко. – М. : Издательство «Экзамен», 2015. – 686, с. (Серия «Банк заданий ЕГЭ»)
4) Математичка — портал [Электронный ресурс]. — Режим доступа: http://mathematichka.ru/, свободный. — Заглавие с экрана.
5) Задачи математических олимпиад / И. Л. Бабинская. – М. : Главная редакция физико-математической литературы издательства «Наука», 1975. – 109, с.
6) Открытый банк задач ЕГЭ по математике — портал [Электронный ресурс]. — Режим доступа: http://base.mathege.ru/, свободный. — Заглавие с экрана.
7) Подготовка к ЕГЭ и ОГЭ — экзамены на олично — портал [Электронный ресурс]. — Режим доступа: http://worksbase.ru/, свободный. — Заглавие с экрана.
Демонстрационный вариант вступительного экзамена
в 8-й математический класс ГБОУ Лицей № 1535. 1 этап
1) Найти значение выражения:
На рисунке изображен график движения туриста из города A в город B, причём по дороге им был сделан привал. Определить:
а) На каком расстоянии (в км) от города A турист сделал привал?
б) Какой была скорость туриста (в км/ч) после привала?
в) Какой была средняяскорость движения туриста (в км/ч) при движении из A в B?
Решение: а) ответ: 9; б) 18-9=9, 7-5=2, значит 9:2=4,5 км/ч; в) 18:5=3,6 км/ч.
3) Привести многочлен (p+3)(p+4)(p-4)-p((1-p)(-p)-16) к стандартному виду/
Решение: (p+3)(p+4)(p-4)-p((1-p)(-p)-16)=(p+3)(p 2 -16)-p(p 2 -p-16)=p 3 +3p 2 -16p-48- p 3 +p 2 +16p=4p 2 -48
4) Найти корень уравнения выражения: 8 15: x=4 17 · 2 6
Решение: 
5) Пользуясь данными рисунка найти градусную меру угла α

Решение: 136°+44°=180°, значит, прямые параллельны. Следовательно, ∠ CBA=44°, ∠ BCA=56°, значит, ∠α=180°-44°-56°=80°.
6) Чему равен корень уравнения
Решение: умножаем все слагаемые на 30, знаменатели сократятся: 
7) Найти значение числового выражения: 
Решение:
8) Если одну из смежных сторон квадрата уменьшить на 2 см, а вторую — увеличить на 6 см, то получится прямоугольник, площадь которого равна площади прямоугольника, который получится из того же исходного квадрата, если одну из его смежных сторон не изменять, а другую увеличить на 3 см. Чему (в квадратных сантиметрах) равна площадь исходного квадрата?
Решение. Пусть x — сторона квадрата. Составим уравнение:
(x -2)(x +6)=x (x +3);
x 2 +4x -12=x 2 +3x ;
x =12
Площадь исходного квадрата равна 12 · 12=144 см 2 .
9) Задать формулой линейную функцию, график которой в системе координат 0xy проходит через точку Т(209,908) и не пересекается с графиком уравнения 9x+3y=14
Решение. Перепишем уравнение в виде
Формула линейной функции в общем виде y=kx+b. Если график искомой не пересекается с графиком данного уравнения, значит k=-3. Следовательно, 908=-3 · 209 + b, откуда b=1535.
Формула искомой линейной функции: y=-3x+1535
10) Имеется кусок сплава меди с оловом общей массой 24 кг, содержащий 45 % меди. Сколько килограммов чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40 % меди?
Решение. Если в сплаве меди с оловом 45 % меди, то значит, в нем 55 % олова. Если в новом сплаве 40 % меди, значит, в нем 60 % олова. Пусть x — количество кг чистого олова, которого надо прибавить к сплаву. Составим уравнение:
0,55 · 24 + x = 0,6 (x+24)
x-0,6x=0,6 · 24- 0,55 · 24
0,4x=0,05 · 24
x=3
Ответ: 3 кг.
Примечание репетитора по математике: подробнее о методах решения задач на сплавы и смеси можно почитать в статье Преимущества и недостатки различных методик решения задач на сплавы и смеси
11) По данным рисунка, на котором изображены графики двух линейных функций и парабола, найти абсциссу точки T. 
Решение. Прямая y=5x и парабола y=x 2 пересекаются в двух точках. Найдем абсциссы этих точек с помощью уравнения 5x=x 2 . Отсюда x 1 =0; x 2 =5. Значит, ордината точки пересечения равна 25
Прямая, на которой лежит точка T, проходит через точки с координатами (5;25) и (0;27). Уравнение прямой в общем виде: y=kx+b. Подставляя вместо x и y координаты точек прямой, получаем систему уравнений:
Точка T имеет ординату, равную нулю. Следовательно
Ответ. 67,5.
12) Из точки А круговой трассы одновременно начинают равномерное движение в противоположных направлениях два объекта. Первый объект к моменту их встречи проходит на 100 метров больше, чем второй, и возвращается в точку А через 9 минут после встречи. Найти длину трассы в метрах, если второй объект возвращается в точку А через 16 минут после встречи.
Примечание. В Интернете можно встретить сайты, где такого рода задачи решаются квадратным уравнением. Между тем, данная работа предназначена для поступающих в 8-й класс. То есть решать эту задачу, зная квадратное уравнение, которое проходят в 8-м классе, некорректно. Ни к чему пременять программу 8-го класса для решения задачи, адресованной семиклассникам. Ниже представлено решение, которое не требует квадратного уравнения
Решение. Пусть t — время до встречи объектов, v 1 — скорость первого объекта, v 2 — скорость второго объекта.
Тогда v 1 · t — v 2 · t = 100, так как на момент встречи первый объект прошел на 100 м больше. Так как v 2 t — путь, который прошел 1-й объект после встречи, v 1 — его скорость и вернулся он в точку А через 9 минут, то можно составить уравнение
Аналогично
. Три уравнения образуют собой систему трех уравнений с тремя неизвестными:
Поделим 1-е уравнение на 2-е. Получится: 
откуда
Подставив это выражение в первое уравнение, получим t=12 мин
Подставив последнее выражение и t=12 в третье уравнение системы, получим:
отсюда 
Согласно условию длину трассы в метрах можно определить, сложив путь первого объекта до встречи и путь второго объекта до встречи. То есть
Ответ. 700 метров
13) На стороне ML квадрата MNKL построен равносторонний треугольник MPL, причём точка P расположена внутри квадрата. Найти градусную меру угла LPK.
Решение
По условию ML=PL=KL; треугольник PLM — равносторонний, значит, все углы равны 60°, значит, ∠ PLK=30°. Таким образом, ∠LPK=(180°-30°) : 2=75°.
14) Разложить на множители: (решения написаны сразу же)
Александр Анатольевич, репетитор по математике. 8-968-423-9589. Имею успешный опыт подготовки учеников в этот лицей, в том числе и в 8-й класс математической специализации и в классы других специализаций. Готовящимся к поступлению в лицей № 1535, равно как и в другие лицеи, важно понимать, что реальные варианты на вступительных экзаменах несколько отличаются от демонстрационных. Поэтому необходимо уметь решать и другие похожие задания.
Источник















