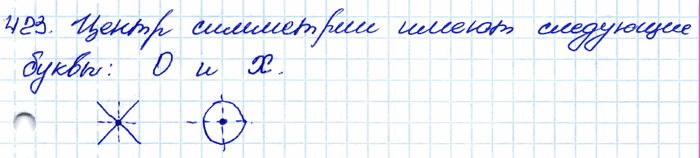Что значит диагонали имеют общую середину

Применение теоремы Вариньона к решению задач

2. 2. Применение теоремы Вариньона к решению задач.

Рассмотрим применение теоремы Вариньона к решению планиметрических задач повышенной трудности. Дело в том, что планиметрические задачи на олимпиадах встречаются значительно чаще.

Мы будем называть параллелограмм KLMN параллелограммом Вариньона, а отрезки КМ и LN, соединяющие середины противоположных сторон четырёхугольника АВСD — средними линиями этого четырёхугольника.

Задача 1. В выпуклом пятиугольнике ABCDE середины сторон AB и CD, BC и DE соединены отрезками. K, L – середины этих отрезков. Доказать, что отрезок KL параллелен пятой стороне AE и составляет ¼ от неё.

Решение: отрежем четырёхугольник ABCD и пусть Р-середина AD, тогда по теореме Вариньона A1B1C1P – параллелограмм, А1С1 – его диагональ и К – середина А1С1, значит, К – середина и второй

диагонали параллелограмма В1Р. Значит, KL – средняя линия треугольника PB1D1, поэтому KL||PD1 и KL=1/2 PD1, но PD1 – средняя линия треугольника ADE, значит, PD1||AE и PD1=1/2AE, поэтому KL||AE и KL=1/4 AE.

Задача 2. Верно ли, что можно составить треугольник из любой средней линии треугольника и отрезков, вдвое меньших его диагоналей?

Решение: верно, так как параллелограмм Вариньона существует для любого выпуклого четырёхугольника. Например, условию задачи удовлетворяют треугольники KLM и LMN на рис. 10. рис. 10

Задача 3. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60˚. Найдите диагонали четырёхугольника.

Решение: пусть KM=a, LN=b, (рис. 10). Тогда NM=, а LT=.

Из треугольника LTM по теореме косинусов . Но LM= BD, поэтому , откуда BD=. Аналогично из треугольника TNM найдём MN, потом вычислим AC: AC=.

Ответ: ;

Задача 4. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.

Доказательство: в параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов рис. 11 диагоналей равна сумме квадратов всех его сторон, т. е. Учитывая, что KL=1/2 AC и LM= 1/2 BD (рис. 11), получим: KM2+LN2=1/2(AC2+BD2), AC2+BD2=2(KM2+LN2).

Задача 5. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.

Доказательство: (рис. 12).

Учитывая, что , KL=1/2 AC и KN=1/2 BD, получим: рис. 12

.

Задача 6. Докажите, что все четырёхугольники, имеющие общие середины

Доказательство: действительно, для всех таких четырёхугольников определён один и тот же параллелограмм Вариньона. Его площадь равна половине площади каждого из исходных четырёхугольников (задача 5), тем самым их равновеликость доказана.

Задача 7. Докажите, что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.

Доказательство: в случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис. 13), а рис. 13

площадь ромба равна половине произведения диагоналей:

, тогда .

Задача 8. Диагонали четырёхугольника ABCD равны d1 и d2, а средние линии равны между собой. Найдите площадь четырёхугольника.

Решение: из условия задачи следует, что в параллелограмме Вариньона диагонали KM и LN равны (рис. 12). Значит, KLMN – прямоугольник и SKLMN=1/2 d1d2, а с другой стороны, SKLMN=1/2 SABCD, следовательно, SABCD=1/2d1d2.

Ответ: SABCD=1/2d1d2.

Задача 9. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.

Доказательство: согласно рис. 14 необходимо доказать, рис. 14

что . Треугольник KLN представляет собой половину параллелограмма Вариньона. (). Так как KL=1/2AC, то , значит, , а с другой стороны, (см. задачу 8), тогда .

Задача 10. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середину его диагоналей.

Доказательство: согласно рис. 11 надо доказать, что. Для медианы ET треугольника ELN имеем: , где , , откуда . Аналогично, выразив медиану FT треугольника KFM и учитывая, что и , получим: .

Кроме того, (задача 7).

Итак, получаем: , откуда:

Задача 11. Постройте трапецию по диагоналям, одному из углов и отрезку, соединяющему середины оснований.

Решение: пусть в трапеции ABCD, которую необходимо построить, известны длины диагоналей AC и BD, отрезка LN и величина угла А (рис. 15).

Поскольку и , нетрудно построить по трём рис. 15

сторонам треугольник KLN. Далее построим его до параллелограмма Вариньона. Затем на отрезке KN построим сегмент, вмещающий угол А, и проведём через точку N параллельно KM прямую, она пересечёт сегмент в точке А. Дальнейшее построение очевидно.

В ходе работы мы прорешали более двадцати пяти задач, формулировки и решения наиболее интересных из них дополнительно приведены в приложении. Мы убедились в том, что теорема Вариньона помогает красиво, оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников.

Источник

Дан четырехугольник ABCD, в котором диагонали имеют общую середину. На продолжении стороны AD за вершину D взята точка Е, DC = ЕС. Докажите

В 1:05 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Вопрос вызвавший трудности

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Дан четырехугольник ABCD, в котором диагонали имеют общую середину. На продолжении стороны AD за вершину D взята точка Е, DC = ЕС. Докажите, что четырехугольник АВСЕ является равнобедренной трапецией

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Суворова Альвина Валерьевна — автор студенческих работ, заработанная сумма за прошлый месяц 64 600 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

Источник

Геометрия 8 класс Атанасян Задачи 399-423

Упражнения 399 — 423 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.

Нажмите на спойлер, чтобы посмотреть ответ на задание.

Геометрия 8 класс Атанасян
Глава 5. § 3. Прямоугольник, ромб, квадрат
Задачи №№ 399 — 423:

Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.

Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.

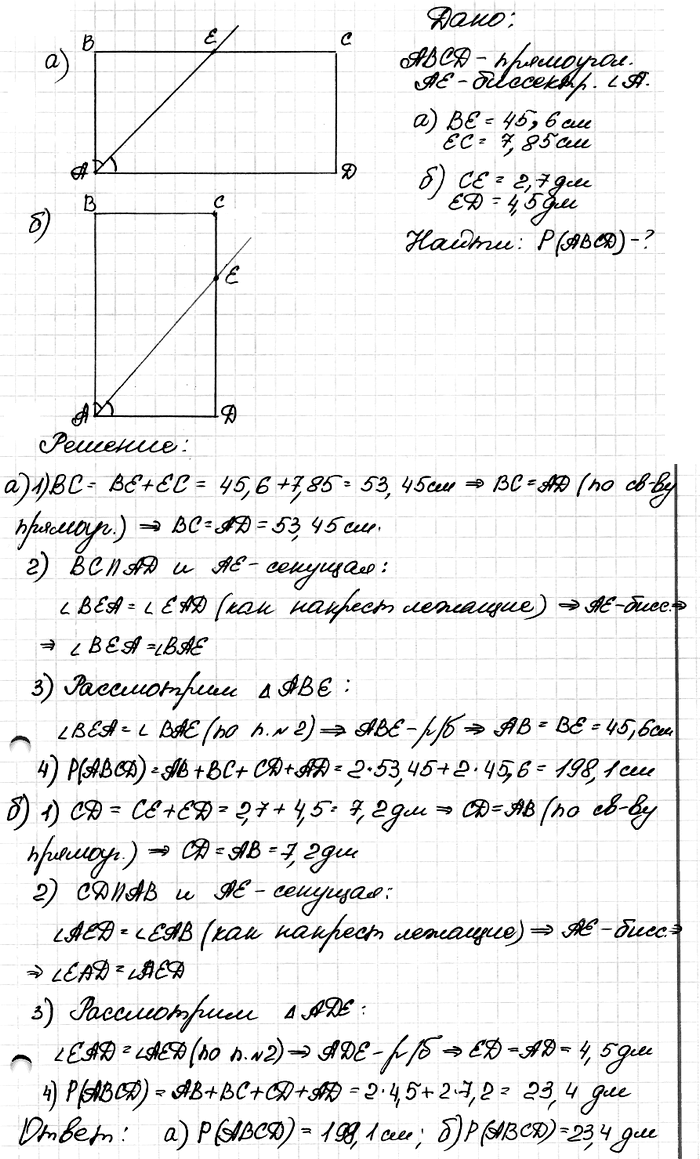
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.

Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.

Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.

Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.

Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.

Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.

Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.

Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.

Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.

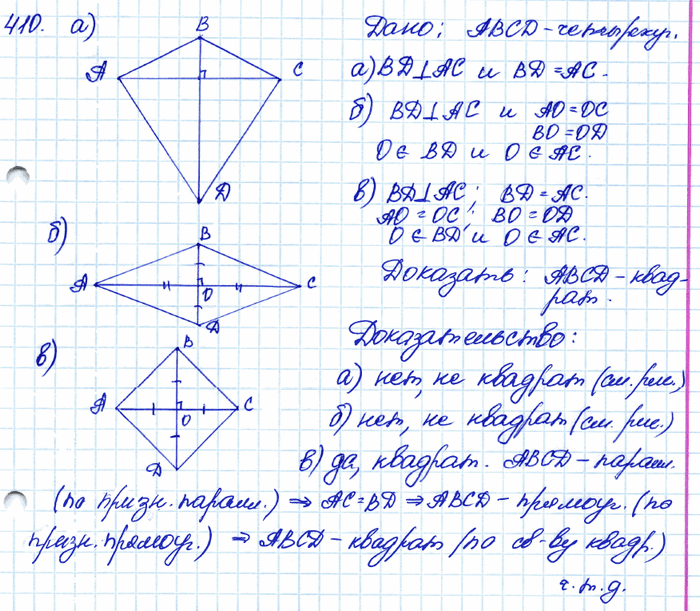
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?

Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.

Задача № 412. Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.

Задача № 413. □ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.

Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.

Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.

Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.

Задача № 417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?

Задача № 418. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F ?

Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.

Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.

Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.

Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?

Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?

Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.

Источник