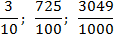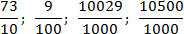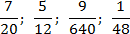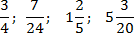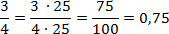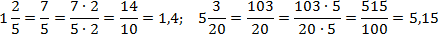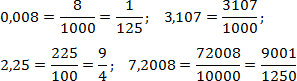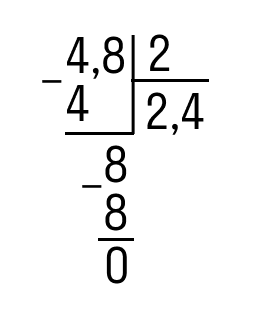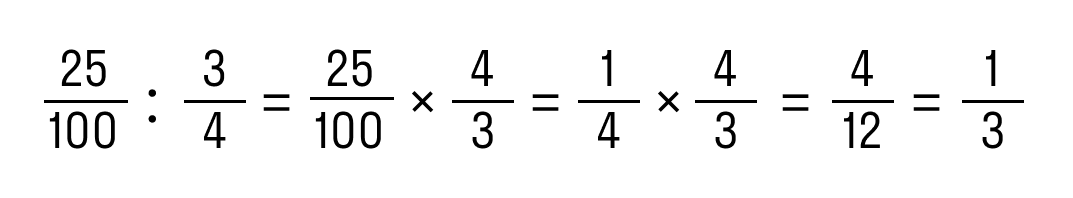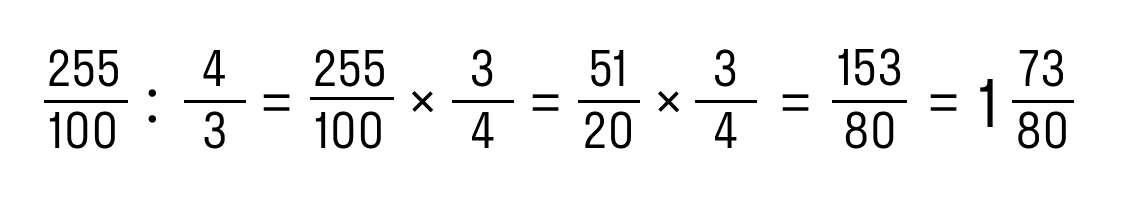Что значит десятичная форма

Цифры. Десятичная запись натуральных чисел

Как здания строят из кирпичей, а слова складывают из букв, так натуральные числа записывают с помощью специальных знаков, которые называют цифрами . Этих цифр десять:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

Натуральные числа, записанные одной цифрой, называют однозначными, двумя цифрами − двузначными , тремя цифрами − трехзначными и т.д. Все числа, кроме однозначных, называют многозначными. Многозначное число может начинаться с любой цифры, кроме цифр 0 .

Легко прочитать трехзначное число 917, однако число 17025543607 прочитать намного сложнее. Чтобы прочитать многозначное число, цифры его записи разбивают справа налево на группы по три цифры: 17 025 543 607 (при этом крайняя слева группа может состоять из трех цифр, из двух, как в данном примере, или из одной цифры). Эти группы называют классами . Первый справа класс называют классом единиц , второй справа − классом тысяч , третий − классом миллионов , четвертый − классом миллиардов и т.д.

При чтении многозначного числа число, записанное в каждом классе, читают как трехзначное, двузначное или однозначное, добавляя при этом название класса (как правило, название класса единиц не произносят). Число 17 025 543 607 читают: » 17 миллиардов 25 миллионов 543 тысячи 607 «.

Каждый класс разбивается справа налево на три разряда : единицы, десятки, сотни.

Так в приведенном примере в классе единиц 7 единиц, 0 десятков, 6 сотен, а в классе миллионов − 5 единиц, 2 десятка, 0 сотен. Названия всех разрядов числа 17 025 543 607 приведены в следующей таблице.

Запись натуральных чисел, который мы пользуемся, называют десятичной . Такое название связано с тем, что десять единиц каждого разряда составляют одну единицу следующего разряда, старшего разряда. Например, десять единиц составляют один десяток, десять десятков − одну сотню и т.д.

Число 2 958 можно представить в виде суммы:

2 958 = 2 000 + 900 + 50 + 8

2 958 = 2 * 1 000 + 9 * 100 + 5 * 10 + 8 * 1 .

Последнее равенство называют записью числа 2 958 в виде суммы разрядных слагаемых.

Источник

Десятичные дроби

14 августа 2011

Из множества дробей, встречающихся в арифметике, отдельного внимания заслуживают такие, у которых в знаменателе стоит 10, 100, 1000 — в общем, любая степень десятки. У этих дробей есть специальное название и форма записи.

— это любая числовая дробь, в знаменателе которой стоит степень десятки.

Примеры десятичных дробей:

Зачем вообще потребовалось выделять такие дроби? Почему для них нужна собственная форма записи? На то есть как минимум три причины:

1. Десятичные дроби намного удобнее сравнивать. Вспомните: для сравнения обычных дробей их требуется вычесть друг из друга и, в частности, привести дроби к общему знаменателю. В десятичных дробях ничего подобного не требуется;
2. Сокращение вычислений. Десятичные дроби складываются и умножаются по собственным правилам, и после небольшой тренировки вы будете работать с ними намного быстрее, чем с обычными;
3. Удобство записи. В отличие от обычных дробей, десятичные записываются в одну строчку без потери наглядности.

Большинство калькуляторов также дают ответы именно в десятичных дробях. В некоторых случаях другой формат записи может привести к проблемам. Например, что, если потребовать в магазине сдачу в размере

Правила записи десятичных дробей

Основное преимущество десятичных дробей — удобная и наглядная запись. А именно:

— это форма записи десятичных дробей, где целая часть отделяется от дробной с помощью обычной точки или запятой. При этом сам разделитель (точка или запятая) называется .

Например, 0,3 (читается: «ноль целых, 3 десятых»); 7,25 (7 целых, 25 сотых); 3,049 (3 целых, 49 тысячных). Все примеры взяты из предыдущего определения.

На письме в качестве десятичной точки обычно используется запятая. Здесь и далее на всем сайте тоже будет использоваться именно запятая.

Чтобы записать произвольную десятичную дробь в указанной форме, надо выполнить три простых шага:

1. Выписать отдельно числитель;
2. Сдвинуть десятичную точку влево на столько знаков, сколько нулей содержит знаменатель. Считать, что изначально десятичная точка стоит справа от всех цифр;
3. Если десятичная точка сдвинулась, а после нее в конце записи остались нули, их надо зачеркнуть.

Бывает, что на втором шаге у числителя не хватает цифр для завершения сдвига. В этом случае недостающие позиции заполняются нулями. Да и вообще, слева от любого числа можно без ущерба для здоровья приписывать любое количество нулей. Это некрасиво, но иногда полезно.

На первый взгляд, данный алгоритм может показаться довольно сложным. На самом деле все очень и очень просто — надо лишь немного потренироваться. Взгляните на примеры:

Задача. Для каждой дроби укажите ее десятичную запись:

Числитель первой дроби: 73. Сдвигаем десятичную точку на один знак (т.к. в знаменателе стоит 10) — получаем 7,3.

Числитель второй дроби: 9. Сдвигаем десятичную точку на два знака (т.к. в знаменателе стоит 100) — получаем 0,09. Пришлось дописать один ноль после десятичной точки и еще один — перед ней, чтобы не оставлять странную запись вида «,09».

Числитель третьей дроби: 10029. Сдвигаем десятичную точку на три знака (т.к. в знаменателе стоит 1000) — получим 10,029.

Числитель последней дроби: 10500. Снова сдвигаем точку на три знака — получим 10,500. В конце числа образовались лишние нули. Зачеркиваем их — получаем 10,5.

Обратите внимание на два последних примера: числа 10,029 и 10,5. Согласно правилам, нули справа надо зачеркнуть, как это сделано в последнем примере. Однако ни в коем случае нельзя поступать так с нулями, стоящими внутри числа (которые окружены другими цифрами). Именно поэтому мы получили 10,029 и 10,5, а не 1,29 и 1,5.

Итак, с определением и формой записи десятичных дробей разобрались. Теперь выясним, как переводить обычные дроби в десятичные — и наоборот.

Переход от обычных дробей к десятичным

Рассмотрим простую числовую дробь вида a / b . Можно воспользоваться основным свойством дроби и умножить числитель и знаменатель на такое число, чтобы внизу получилась степень десятки. Но прежде, чем это делать, прочитайте следующее:

Существуют знаменатели, которые не приводятся к степени десятки. Учитесь распознавать такие дроби, потому что с ними нельзя работать по алгоритму, описанному ниже.

Вот такие дела. Ну и как понять, приводится знаменатель к степени десятки или нет?

Ответ прост: разложите знаменатель на простые множители. Если в разложении присутствуют только множители 2 и 5, это число можно привести к степени десятки. Если найдутся другие числа (3, 7, 11 — что угодно), о степени десятки можно забыть.

Задача. Проверить, можно ли представить указанные дроби в виде десятичных:

Выпишем и разложим на множители знаменатели этих дробей:

Следовательно, дробь можно представить в виде десятичной.

Дробь не представима в виде десятичной.

Все в порядке: кроме чисел 2 и 5 ничего нет. Дробь представима в виде десятичной.

Снова «всплыл» множитель 3. Представить в виде десятичной дроби нельзя.

Итак, со знаменателем разобрались — теперь рассмотрим весь алгоритм перехода к десятичным дробям:

1. Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;
2. Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.
3. Собственно, умножить числитель и знаменатель исходной дроби на этот множитель — получим искомое представление, т.е. в знаменателе будет стоять степень десятки.

Разумеется, дополнительный множитель тоже будет разлагаться только на двойки и пятерки. При этом, чтобы не усложнять себе жизнь, следует выбирать наименьший такой множитель из всех возможных.

И еще: если в исходной дроби присутствует целая часть, обязательно переведите эту дробь в неправильную — и только затем применяйте описанный алгоритм.

Задача. Перевести данные числовые дроби в десятичные:

Разложим на множители знаменатель первой дроби: Следовательно, дробь представима в виде десятичной. В разложении присутствуют две двойки и ни одной пятерки, поэтому дополнительный множитель равен С ним количество двоек и пятерок сравняется. Имеем:

Теперь разберемся со второй дробью. Для этого заметим, что в разложении присутствует тройка, поэтому дробь не представима в виде десятичной.

Две последних дроби имеют знаменатели 5 (простое число) соответственно — везде присутствуют только двойки и пятерки. При этом в первом случае «для полного счастья» не хватает множителя 2, а во втором — 5. Получаем:

Переход от десятичных дробей к обычным

Обратное преобразование — от десятичной формы записи к обычной — выполняется намного проще. Здесь нет ограничений и специальных проверок, поэтому перевести десятичную дробь в классическую «двухэтажную» можно всегда.

Алгоритм перевода следующий:

1. Зачеркните все нули, стоящие в десятичной дроби слева, а также десятичную точку. Это будет числитель искомой дроби. Главное — не переусердствуйте и не зачеркните внутренние нули, окруженные другими цифрами;
2. Подсчитайте, сколько знаков стоит в исходной десятичной дроби после запятой. Возьмите цифру 1 и припишите справа столько нулей, сколько знаков вы насчитали. Это будет знаменатель;
3. Собственно, запишите дробь, числитель и знаменатель которой мы только что нашли. По возможности, сократите. Если в исходной дроби присутствовала целая часть, сейчас мы получим неправильную дробь, что очень удобно для дальнейших вычислений.

Задача. Перевести десятичные дроби в обычные:

Зачеркнем нули слева и запятые — получим следующие числа (это будут числители):

В первой и во второй дробях после запятой стоит по 3 знака, во второй — 2, а в третьей — целых 4 знака. Получим знаменатели:

Наконец, объединим числители и знаменатели в обычные дроби:

Как видно из примеров, полученную дробь очень часто можно сократить. Еще раз отмечу, что любая десятичная дробь представима в виде обычной. Обратное преобразование можно выполнить не всегда.

Источник

Страна математических знаний. 5 класс

Всегда ли вы понимаете, что написано в учебниках по математике? Бывает ли так, что возникает потребность несколько раз перечитать задание? Бывает ли так, что вы пропустили несколько тем, а потом не можете догнать материал?Эта книга может пригодиться вам в каждой подобной ситуации и стать надежным помощником при изучении математики в 5 классе.Успехов в изучении!

Оглавление

• Ар
• Биссектриса угла
• Боковые стороны равнобедренного треугольника
• Буква в математике
• Буквенное выражение
• Величина
• Вершина куба
• Вершина равнобедренного треугольника
• Вершина угла
• Вершина четырехугольника
• Вершина ломаной линии
• Выделить целую часть в неправильной дроби
• Выполнить действия
• Высота фигуры
• Вычислить
• Вычислить значение выражения
• Вычитаемое
• Вычитание
• Вычитание десятичных дробей в столбик
• Вычитание дробей с одинаковым знаменателем
• Вычитание подобных одночленов
• Гектар
• Градус
• Градусная мера угла
• Грамм
• Грань куба
• Двойное неравенство
• Двузначное число
• Деление
• Деление десятичной дроби на 0,1
• Деление десятичной дроби на 10
• Деление десятичной дроби на число
• Деление десятичных дробей
• Деление дробей
• Деление с остатком
• Деление числа на десятичную дробь
• Делимое число
• Делитель
• Десятичная дробь
• Десятичная запись натурального числа
• Десяток
• Десяток
• Дециметр
• Длина
• Длина
• Длина ломаной линии
• Длина отрезка
• Дополняющие лучи
• Дробная часть смешанного числа
• Дробное число
• Единица
• Единица
• Единица длины
• Единичный квадрат
• Единичный куб
• Единичный отрезок
• Единичный угол
• Задача
• Замкнутая ломаная линия
• Записать цифрами число
• Запись натурального числа в виде суммы разрядных слагаемых
• Звенья ломаной линии
• Знак
• Знак неравенства
• Знак больше
• Знак меньше

Приведённый ознакомительный фрагмент книги Страна математических знаний. 5 класс предоставлен нашим книжным партнёром — компанией ЛитРес.

Источник

Десятичные дроби

О чем эта статья:

5 класс, 6 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6
• 21,10200000 = 21,102

Основные свойства
Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Пример 2. Перевести 37/1000 в десятичную дробь.

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

Источник