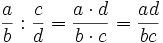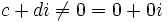Что значит делимое число

Деление чисел

Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.

Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:

Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:

2 + 2 + 2 = 2 · 3 = 6.

Для записи деления используется знак : (двоеточие), который ставится между числами. Например:

Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (равно), после которого записывается полученный результат:

Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?

Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.

Решение можно записать так:

Пример. Решить примеры на деление с помощью схем.

2) 12 : 4 = 3, 12: 3 = 4.

Делимое, делитель и частное

Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:

12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.

Частное — это число, которое получается в результате деления. Например, в записи:

4 — это частное. При этом сама запись 12 : 3 тоже называется частным.

Эта запись читается так: частное двенадцати и трёх равняется четырём или двенадцать разделить на три равно четырём .

Проверка деления

где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:

Умножить частное на делитель:

или умножить делитель на частное:

если получится делимое, то деление было выполнено верно.
Разделить делимое на частное, если получиться делитель, то деление было выполнено верно:

Источник

Делимое

Деле́ние (операция деления) — это одно из четырёх простейших арифметических действий, обратное умножению.

Подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание.

Рассмотрим, например, такой вопрос:

сколько раз 3 содержится в 14?

Повторяя операцию вычитания 3 из 14, мы находим, что 3 «входит» в 14 четыре раза, и еще «остаётся» число 2

Результат деления также называют отношением.

Содержание

Деление натуральных чисел

Деление не замкнуто в кольце целых чисел. Простым языком это означает то, что деление одного целого числа на другое может не быть целым. В случае, если всё-таки результат является целым числом, говорят о делении без остатка.

Деление чисел издавна считалось самой трудной из арифметических операций. Было время, когда «секрет» деления знало не очень много посвящённых людей, и буквально передавало из поколения в поколение. Происходило это потому, что существовавшие алгоритмы деления были очень громоздки, сложны для исполнения и запоминания (например, деление в виде корабля). Появление деления столбиком радикально изменило эту ситуацию — теперь деление входит в раннюю школьную программу по математике наряду с остальными арифметическими действиями. Однако так же, как и в случае с умножением, в последнее время открыты более эффективные алгоритмы (см. en:Division (digital), применяющиеся в вычислительной технике.

Существуют правила, позволяющие быстро определить, делится ли число на заданный делитель без остатка (признаки делимости). Наиболее известные признаки делимости на 2, 3, 4, 5, 8, 9, 11, 25 и их производные, также существует признаки делимости на 7, 13, 1001 и другие числа.

Целое число, на которое одновременно делятся без остатка несколько чисел, называется их общим делителем.

Определение количества делителей натурального числа приводит к двум важным понятиям: составное и простое число. У простого числа есть только два делителя — 1 и само число.

В случае, если одно натуральное число не делится на другое без остатка, можно говорить о делении с остатком. Рассмотрение остатков, их сравнение и формализация в виде вычетов привели к целой науке — теории чисел.

Обычно на остаток накладываются следующие ограничения (чтобы он был корректно, т.е. однозначно, определён):

. .

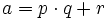
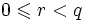
Где a — делимое, p — делитель, q — частное и r — остаток.

Деление целых чисел

Деление произвольных целых чисел не существенно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.

Однако деление целых чисел с остатком определяется по-разному. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, − 7 / ( − 3) = 2 с остатком (-1)); в другом случае понятие остатка напрямую обобщается и ограничения заимствуются из натуральных чисел:

.

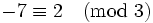
Деление рациональных чисел

Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).

Правило деления обыкновенных дробей:

Деление вещественных чисел

Деление также замкнуто в поле ненулевых вещественных чисел. Сечение Дедекинда позволяет однозначно определить результат деления.

Деление комплексных чисел

Комплексные числа опять замкнуты относительно операции деления.

• В алгебраическое форме результат можно получить путём домножения на сопряжённое число:

. Результат определён для всех

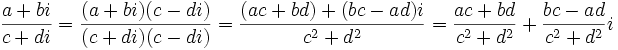
• В экспоненциальной форме легче всего получить результат:

. Видно, что при этом модули делятся, а аргументы вычитаются.

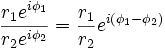
• Аналогично в тригонометрической форме:

.

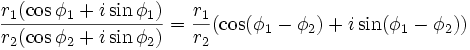
Деление в алгебре

В отличие от простейших арифметических случаев на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.

Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым ( x − 1 * x = e ), так и правым ( x * x − 1 = e ). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

.

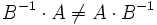
Отношение тензоров в общем случае не определено.

Деление многочленов

В общих чертах оно повторяет идеи деления натуральных чисел, ибо натуральное число есть ничто иное как значения многочлена, у которого коэффициенты — цифры, а вместо переменной стоит основание системы счисления:

.

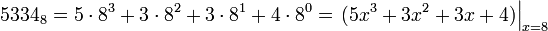
Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.

Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.

Деление на ноль

По правилам арифметики деление на число 0 запрещено, поскольку оно приводит к противоречию. Другое дело — деление на бесконечно малую функцию или последовательность (которые можно считать «нулями» в соответствующих множествах). Деление конечных функций на бесконечно малые приводит к появлению бесконечно больших, а отношение двух бесконечно малых называется неопределённостью 0/0, которую можно преобразовать (см. раскрытие неопределённостей) с тем, чтобы получить определённый результат.

Источник

Делитель и делимое числа.
Делимость суммы и разности числа.

Операции сложения и умножения всегда возможно, но операции вычитания и деления без остатка возможны только при определенных условиях. В вычитании мы можем легко увидеть, возможно это или нет: достаточно, чтобы уменьшаемое было больше или равно вычитаемому. В делении не всегда просто увидеть, делится ли число без остатка. Есть определенные случаи деления, в которых, используя некоторые признаки числа, мы можем увидеть заранее, можно ли деление сделать без остатка или нет.

Делитель и делимое

Если число может быть разделено на другое без остатка, мы говорим, что первое число делимое или что оно делится на второе, а второе — это делитель первого числа.

Например: число 8 делится на 4 , и 4 это делитель 8. Но 8 не делится на 3 и 3 не является делителем 8.

15 делится на 1, 3, 5, 15, и каждое из этих чисел — делитель 15

Каждый число делится на себя. 1 есть делителем для всех чисел. Например: 4/4 = 1; 7/7 = 1; 9/1 = 1; 12/1 = 12

Делимость суммы числа

Числа 6 и 14 делятся на 2; их сумма 20 также делится на 2.
Числа 12, 18, 30 делятся на 6; их сумма 60 делится на 6

Мы можем использовать это свойство, чтобы определить, делится ли одно число на другое, не проводя операции деления

Например: Делится ли число 742 на 7?
Для ответа на вопрос, запишем 742 в виде суммы слагаемых: 742 = 700 + 42. Поскольку оба числа 700 и 42 делится на 7, то их сумма 742 также делится на 7.

15 делится на 3, а 10 не делится на 3. Их сумма 25 не делится на 3

10 и 30 делятся на 5, но 8 не делится на 5 и их сумма 48 также не делится на 5

Делимость разности числа

40 и 12 делится на 4. Их разница 28 делится на 4.

Мы используем это свойство, чтобы определить, делится ли одно число на другое, не проводя операции деления
Например: Делится ли 792 на 8? Если к этому числу добавить 8, мы получаем 800 или 800 — 8 = 792

Уменьшаемое (800) и вычитаемое (8), делится на 8, поэтому разница 792 делится на 8 также

40 делится на 10, но 12 не делится на 10. Их разница 28 не делится на 10 также

40 не делится на 6, а 12 делится на 6. Их разница 28 не делится на 6 также

Источник

Признаки делимости чисел

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

• Число «0» считается четным числом.

• 0, 8, 24, 66, 88, 100, 120 — чётные.

• 1, 7, 31, 75, 91, 111, 311 — нечётные.

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

• Число 51352 можно разделить на 2, так как последняя цифра (2) делится на 2 без остатка.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

• 20715 можно поделить на 3, так как 2 + 0 + 7 + 1 + 5 = 15 делится на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

• 84100 делится на 4, так как в конце стоят два нуля.
• Число 5324 и 1108 тоже делятся на 4, так как последние цифры образуют числа (24 и 08), которые делятся на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

• 540 и 545 делятся на 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

• Число 612 делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

• 43000 делится на 8, так как 43(000) оканчивается нулями
• 8128 — тоже делится на 8: последние три цифры образуют число 128, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

• 1737 — сумма цифр 1 + 7 + 3 + 7 = 18. 18 делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

• 890 делится на 10.
• 1200 делится на 100.

У нас есть очень крутая статья — деление в столбик, возможно тебе будет интересно!

Источник