Что значит что треугольник искомый

Большая Энциклопедия Нефти и Газа

Искомый треугольник

Предположим, что искомый треугольник построен и С — вершина его прямого угла. Так как / — АС В — 90, точка С лежит на окружности S с диаметром АВ. Поэтому точка С является точкой пересечения окружности S и данной окружности. Построив точку С и проведя прямые С А и АВ, найдем оставшиеся вершины искомого треугольника. [16]

По этим данным искомый треугольник ВАС может быть построен. [17]

Предположим, что искомый треугольник ABC построен. [19]

Третьей вершиной А искомого треугольника буает , очевидно, точка пересечения этой дуги с большим кругом, перпендикулярным к дуге ВС и проходящим через ее середину. Задача всегда имеет одно решение. [20]

Вершины А и В искомого треугольника легко построить. Значит, задача сводится к построению вершины С. [21]

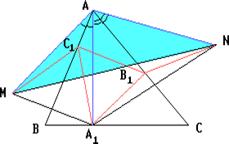
Согласно дополнительному требованию задачи, искомый треугольник должен быть расположен на плоскости так, чтобы он имел общий угол с данным треугольником ABC. Отложим от его вершины на Л С отрезок ACib и проведем прямую CiBi СВ. ДЛС удовлетворяет всем требованиям задачи. [22]

Пересечение этих призм и дает искомый треугольник составов системы . Схематически это показано на фиг. [23]

Пересечение этих призм и дяет искомый треугольник составов системы . Схематически это показано на фиг. [24]

Если данная боковая сторона ВС искомого треугольника меньше квадранта, то задача может иметь два решения, одно решение или не иметь ни одного решения ( черт. Построение треугольника с наибольшей площадью сводится к проведению через точки В и С окружности, касающейся построенной окружности ( упр. [25]

Если данная боковая сторона ВС искомого треугольника раина квадранту, то задача может иметь одно решение или не иметь ни и i-ного решения ( черт. [26]

Это соотношение указывает способ построения искомого треугольника ABC . [27]

Полученный треугольник АгА А3 и есть искомый треугольник . Аналогичное построение можно сделать и в случаях, когда некоторые из углов равны нулю или тт. [28]

В соответствии с анализом легко построить искомый треугольник и доказать, что он удовлетворяет всем требованиям задачи. [29]

И опять, если мы возьмем искомый треугольник заданного вида , то придется искать прямоугольный треугольник такой, чтобы полусумма перпендикулярных сторон, умноженная на себя и увеличенная на шестикратную площадь, давала квадрат. [30]

Источник

Задачи на экстремум в планиметрии

Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .

Отсюда следует, что искомый треугольник — это треугольник с вершинами в основаниях высот данного, т.е. ортотреугольник данного треугольника. Действительно, пусть AA», BB» и CC» — высоты треугольника ABC, а точки A1, B1 и C1 расположены на сторонах соответственно BC, AC и AB. Если треугольник A1B1C1 не совпадает с треугольником A»B»C», то по ранее доказанному

P A1B1C1 PA»B1C1 PA»PQ,

где P и Q — точки пересечения прямой MN со сторонами соответственно AB и AC треугольника ABC. При этом хотя бы один из знаков неравенства — строгий. Значит, искомый треугольник минимального периметра — это треугольник A»PQ. Если бы точка P не совпадала с точкой C», то, повторив предыдущие рассуждения, построили бы треугольник, площадь которого меньше площади треугольника A»PQ, что невозможно. Аналогично для точки Q. Таким образом, точка P совпадает с C», а точка Q — с точкой B».

1. Изложенное решение основано на доказательстве Фейера (L.Fejer). Это, а также другие изящные доказательства данного утверждения (Г.А.Шварц, Л.Шрутка, Бюкнер) см. в книге Г.Радемахера и О.Теплица «Числа и фигуры» (М.,1962, с.36-46).

2. Другой способ доказательства того, что точки P и Q пересечения прямой MN со сторонами соответственно AB и AC также будут основаниями высот треугольника ABC.

Поскольку AM = AA» = AN, то точки M, A» и N лежат на окружности с центром A и радиусом AA». Тогда

A»NP = A»AP

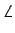
(вписанный угол равен половине соответствующего центрального). Поэтому из точек A и N отрезок A»P виден под одним и тем же углом. Значит, точки A, P, A», N лежат на одной окружности.

С другой стороны, треугольники AA»C и ANC симметричны относительно прямой AC, поэтому они равны. Значит, из точек A» и N отрезок AC виден под прямым углом, поэтому эти точки лежат на окружности с диаметром AC. Поскольку через три точки, не лежащие на одной прямой, проходит ровно одна окружность, то все пять точек A, P, A», C и N лежат на окружности с диаметром AC. Тогда из точки P диаметр AC виден под прямым углом, т.е. CP — высота треугольника ABC. Аналогично докажем, что BQ — также высота треугольника ABC.

В этой курсовой работе я изучила некоторые теоремы, позволяющие решать задачи на экстремумы, проиллюстрировала их применение.

В заключение этой работы, на мой взгляд, следует провести однозначную черту под бесспорным фактом целесообразности и полезности применения ряда задач элементарной геометрии на построение некоторых фигур таким образом, чтобы один из параметров получил наибольшее или наименьшее значение. Во многих случаях решение можно получить без применения методов математического анализа.

1. С.И. Зетель, «Задачи на максимум и минимум», Москва

2. С.А. Теляковский, «Алгебра», Москва, 2001г.

3. Ю.Н. Макарычев, «Математика», Москва, 1988г.

4. Г.С.М. Коксетер, С.П. Грейтцер, «Новые встречи с геометрией», 1978г.

Источник

Задача индийских 9-классников. Наши не решили

У нас есть квадрат с единичной стороной. Жёлтый угол равен 45°, зелёный — 70°. Нужно найти синий угол и периметр зеленого треугольника.

Задача не то, чтобы сложная, но есть нюанс — индийские школьники в 9 классе ещё не знакомы с тригонометрией, так что попробуйте обойтись в решении без неё.

Если хотите подумать сами, то не спешите скролить страничку вниз, а подумайте сами. А если нужны подсказки, то пролистывайте вниз медленно, пункт за пунктом.

Решение

1. Давайте для начала рассмотрим синий треугольник (рисунок ниже). Так как он прямоугольный, а зеленый угол известен по условию, значит, оставшийся третий (синий) угол равен 180°-90°-70°=20°.

2. Теперь посмотрим на угол А квадрата (рисунок ниже). Он равен 90° и образован тремя углами: синим (мы его только что нашли — 20°), жёлтым, который по условию равен 45° и красным. Последний мы можем найти как 90°-45°-20°=25°.

3. Теперь посмотрим на красный треугольник — он прямоугольный. И найдем оставшийся угол. 180°-90°-25°=65°. Запомним этот угол, он нам ещё пригодится. Рисунок ниже.

4. Теперь сделаем финт ушами. Повернем синий треугольник на 90° по часовой стрелке вокруг вершины А (рисунок ниже). Я не могу объяснить, как до этого можно догадаться логически. Наверное, это озарение. Или опыт. Или седьмое чувство. Должно получится так же, как на картинке ниже. Новую вершину обозначим F’, так как это изображение повернутой вершины F. Мы получили конгруэнтный треугольник. Отметим угол 20°.

5. Теперь посмотрим на жёлтый треугольник (рисунок ниже). Угол при вершине А в нём равен 20°+25°=45°. А ещё AF’=AF по построению. А сторона АЕ является общей для желтого и розового треугольников. Из этого следует, что жёлтый и розовый треугольники равны по двум сторонам и углу между ними. По сути они являются отражением друг друга относительно стороны АЕ.

6. Раз жёлтый и розовый треугольники равны, значит, все соответствующие элементы в них тоже равны и искомый синий угол равен красному углу Е (смотри рисунок ниже), который мы находили в третьем пункте, и который равен 65° . Выходит, что на первый вопрос, мы ответили, осталось найти периметр зеленого треугольника.

7. Вспоминаем, что ▲AF’D=▲ABF по построению, а значит, синие отрезки (смотри рисунок ниже) равны — обозначим их за Х. Тогда красный отрезок равен (1-Х). Обозначим жёлтый отрезок за Y.

9. Из равенства жёлтого и розового треугольников (рисунок в пункте 6 — ▲AF’E=▲AEF) следует, что зеленые отрезки (рисунок ниже) равны (X+Y). А оранжевый отрезок равен (1-Y), потому что сторона квадрата равна 1.

10. Поучается, что периметр искомого треугольника равен сумме зеленого, красного и оранжевого отрезков. То есть периметр зеленого треугольника равен (X+Y)+(1-X)+(1-Y)=1+1= 2 . Это и есть ответ на второй вопрос задачи.

Как вам? Удалось решить самостоятельно? Российские девятиклассники, которым я давал эту задачу, не смогли осилить эту задачу. И понятно почему. Как можно было догадаться до того, что треугольник ABF нужно повернуть на 90° по часовой стрелке? Вот как? Я сам до сих пор не понимаю, как это пришло в голову.

Именно за это я и люблю геометрические задачи. Никогда не знаешь с чего начать, что использовать и что бы такое сделать. И каждый раз, находя самостоятельно решение задачи, подобной этой, испытываешь катарсис. Дети, кстати, когда впервые услышали это слово, тихонечко захихикали, как будто я сказал что-то пошлое. А вы, к слову, знаете, что такое катарсис?

Не забывайте подписываться на мои каналы в любимых соцсетях, ссылки на них в описании канала .

Источник

Что значит что треугольник искомый

Предметом нашего исследования являются ортоцентрические треугольники и их свойства.

Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.

1) выяснить, что такое ортотреугольник;

2) изучить и проанализировать свойства ортотреугольников;

3) рассмотреть возможное применение

этих свойств для решения задач.

4) подвести итоги.

Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.

Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.

Глава 1. Исторические сведения и свойства

§ 1. Что такое ортоцентрический треугольник?

Ортотреуго́льник (ортоцентрический треугольник) — это треугольник ΔA_1B1C₁, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) ΔA_1B1C₁ сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника ΔA_1B1C₁.

§ 2. Исторические сведения

В начале 18 века итальянский инженер и математик Фаньяно дей Тоски поставил перед собой такую задачу: вписать в остроугольный треугольник АВС треугольник наименьшего периметра так, чтобы на каждой из сторон данного треугольника лежала одна вершина вписанного. Аналитическое решение этой задачи было опубликовано в 1755 году. Было доказано, что существует единственный треугольник наименьшего периметра KMN, его вершина K – основание высоты CK. Искомым треугольником всегда будет ортотреугольник KMN.

§ 3.Свойства ортотреугольников

1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.

В остроугольном треугольнике проведены высоты , . Найдем углы треугольника , если , а .

Прямоугольные треугольники и имеют общий угол при вершине С, они подобны, поэтому .

Из этого равенства следует, что в треугольниках и стороны, прилежащие к общему углу при вершине С, пропорциональны. Следовательно, по второму признаку подобия треугольников подобен . В подобных треугольниках против соответственных сторон лежат равные углы, поэтому угол , .

Аналогично можно доказать подобие треугольников и ; и , если провести высоту CC₁. При этом , и .

Как следствие данной теоремы, верно следующее утверждение:

Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.

Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.

І. Ортоцентрический треугольник H₁H₂H₃ В остроугольном треугольнике ABC соединим отрезками основания высот H₁,H₂,H₃ (рис. 1). Получим

треугольник H₁H₂H₃. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.

Свойство 1. Стороны ортоцентрического треугольника H₁H₂H₃ антипараллельны сторонам треугольника ABC.

Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH₂HH₃. Тогда ∠AH₂H₃ = ∠AHH₃ = ∠ABC, значит, сторона H₂H₃ антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника

Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H₁H₂H₃.

Свойство 3. Отрезок OA перпендикулярен отрезку H₂H₃.

Доказательство. Действительно, если описать окружность около треугольника H₁H₂H₃, дуги, на которые опираются углы ∠H₂H₁A и ∠AH₁H₃, равны, а значит, OA⊥H₂H₃ (рис. 2).

Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H₁H₂H₃ (рис. 3).

Доказательство. Поскольку отрезок AH₂ перпендикулярен биссектрисе H₂B, а AH₃⊥CH_3, то пересечение отрезков AH₂ и AH₃, — точка A есть центр вневписанной окружности, касающейся стороны H₂H₃.

Свойство 5. Имеет место формула p_H = h_asinA, где p_H — полупериметр треугольника H₁H₂H₃, h_a — высота AH₁.

Доказательство. Из точки A опустим перпендикуляр AF на прямую H₁H₃ (рис.3). Поскольку∠H₁AF = ∠H₃H₁B (углы с взаимно перпендикулярными сторонами), то ∠HAF = ∠A и H₁F = h_asinA (из треугольника H A1 F), или p_H = h_asinA.

Свойство 6. Имеет место формула S = Rp_H, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.

Доказательство. Действительно, поскольку p_H = h_asinA, то

p_H= sinA, и S = Rp_H(a — длина стороны BC).

Свойство 7. Окружность Леонарда Эйлера.

Доказательство. Опишем окружность около треугольника H₁H₂H₃. Докажем, что окружности (обозначим её γ_e), кроме точек H₁, H₂, H₃, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E₁, E₂, E₃), ещё три точки M₁, M₂, M₃ — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).

Поскольку прямая H H1 (рис. 4) принадлежит биссектрисе угла ∠H₂H₁H₃, то точка её пересечения с окружностью γ_e, описанной

около треугольника H₁H₂H₃, будет серединой дуги H₂H₃, то есть точкой W₁ треугольника H₁H₂H₃, а точка A — центром вневписанной

окружности (свойство 4).

По теореме Мансиона ( IW₁ = W₁I_a = W₁B = W₁C): AE₁ = E₁H. Значит, точка совпадает с серединой отрезка IW₁ для треугольника H₁H₂H₃ с точкой E₁. Поскольку точки B и C также центры вневписанных окружностей, то утверждение относительно середин отрезков AH, BH и CH доказано. Докажем, что середины AC, BC и AB (точки M₁, M₂, M₃) принадлежат окружности γ_e.

Воспользуемся свойством вневписанных окружностей с центрами Ib и I_c. Пусть W₁ A — точка, диаметрально противоположная точке W₁. Тогда W₁ A — середина отрезка IbI_c. Пусть окружность γ_e пересекает сторону BC в точке X (рис. 4). Поскольку ∠E₁H₁X₁ = 90°, то точки X и E₁ диаметрально противоположны, а поскольку точка E₁ есть точкой W₁ окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.

ІІ. Ортоудвоенный треугольник

Высоты AH₁, BH₂, CH₃ продолжим до пересечения с описанной окружностью (рис. 5).

Получим треугольник N_1N2N3, который назовём ортоудвоенным. Поскольку HH₁ = H_1N1, HH₂ = H_2N2, HH₃ = H_3N3, то этот треугольник гомотетичен треугольнику H₁H₂H₃ с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =

Свойство 1. Вершины треугольника ABC делят дуги N_2N3, N_3N1, N_1N2 пополам.

Доказательство. Действительно, ∠ N_2N1A = ∠ N_3N1A.

Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N_1N2N3.

Доказательство. Действительно, это следует из свойства 1.

Свойство 3. Радиус OA перпендикулярен отрезкам N_2N3 и H₂H₃.

Доказательство. Действительно, это следует из свойства 1.

Свойство 4. Точка, симметричная ортоцентру H относительно середины M₁ отрезка BC принадлежит окружности, описанной около треугольника

Доказательство. Проведём диаметр AA₁ (рис.6) и найдём точку X, гомотетичную точке A₁. Поскольку A₁X = XH, то отрезок OX — средняя линия треугольника

AA₁H. Значит, он параллелен AH и равен

AH, то есть OX = OM₁ и точка X совпадает с точкой M₁ — серединой отрезка BC.

Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.

Доказательство. Проведём отрезок AM₁ (рис. 6). Он пересечёт OH в точке Y. Поскольку то M₁M : AM = 1 : 2, а значит, точка Y совпадает с точкой M₁.

Окружность девяти точек

Около треугольника H₁H₂H₃ опишем окружность γ_e. Её центр делит пополам отрезок OH (точка E). Середины отрезков AH, BH, CH (точки E₁, E₂, E₃) гомотетичны точкам A, B и C и принадлежат окружности γ_e.

Докажем, что точки M₁, M₂, M₃ принадлежат окружности γ_e.

Доказательство. Действительно, точки A₁ и H симметричны относительно точки B. Кроме того, точки A₁ и M₁ гомотетичны, а значит, точка M₁ принадлежит окружности γ_e.

ІІІ. Ортоцентрический треугольник Q₁Q₂Q₃

Опишем окружность около треугольника ABC и построим точки W₁,W₂, W₃ (середины дуг BC, AC, AB) (рис. 7).

Точку пересечения хорд W₂W₃ и AW₁ обозначим Q₁. Аналогично получим точки Q₁ и Q₃. По теореме «листа трилистника» имеем: IW₁ = W₁C. Поскольку ∪ AW₂ = ∪ W₂C, то

а значит, треугольник Q₁Q₂Q₃ — ортоцентрический треугольник треугольника W₁W₂W₃. В равнобедренном треугольнике IW₁C IQ₃ = Q₃C. Аналогично, IQ₁ = Q₁A, следовательно, стороны треугольника Q₁Q₂Q₃ вдвое меньше соответственных сторон треугольника ABC. Поэтому (применяем формулу S = Rp_H ) площадь треугольника W₁W₂W₃ . (1°)

Поскольку окружность, описанная около треугольника Q₁Q₂Q₃, есть окружность Эйлера треугольника W₁W₂W₃, то девять точек принадлежат одной окружности: середины отрезков W₁W₃, W₂W₃, W₁W₂, IW₁, IW₂, IW₃, IA, IB, IC.

ІV. Ортоцентрический треугольник ABC Рассмотрим треугольник, вершины которого — центры вневписанных окружностей I_a, Ib, I_c (рис.8).

Ортоцентрическим треугольником этого

треугольника будет треугольник ABC, так как

каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника I_aIbI_c будет 2R, а площадь S_IaIbIc=2R⋅p.

Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника I_aIbI_c, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W₁, W₂, W₃, середины

V. Треугольник, подобный ортоцентрическому треугольнику H₁H₂H₃

Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T₁T₂T₃ (рис. 9).

тангенциальным) вычисляют по формуле:

S_T=R⋅p_T, где R — радиус окружности, вписанной в треугольник T₁T₂T₃.

Глава 2. Применение.

§ 1 Применение свойств ортотреугольника для решения задач

Задача 1.

Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

подобен треугольнику АВС по теореме 1. Коэффициент подобия . В прямоугольных треугольниках и , . Значит, .

Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.

Задача 2.

Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ.

Поскольку и — высоты треугольника , треугольник подобен с коэффициентом подобия , поэтому

Задача 3

В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF. Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.

Решение(без применения свойств):

1. Т.к. и согласно задаче 1 , то . ,

Пусть О – центр описанной окружности , R – ее радиус. Тогда Т.к. по т. синусов , то после подстановки, получаем .

Аналогично и , т.е. . Поскольку и , то , что и требовалось доказать.

Решение(без применения свойств):

По свойству 6 . , тогда , что и требовалось доказать.

Задача 4

Треугольник АВС остроугольный, и . Определите углы высотного треугольника.

1. Строим высоты , , .

Задача 5.

Т.к. — равнобедренный, то — высота, медиана, биссектриса ;.

4. Т.к. подобен , то; .

5. ||, а это значит, что подобен .

7. По т. Пифагора .

Задача 6

В равнобедренном треугольнике ABC(AB = BC)проведены высоты AA₁,

Т.к. подобен , то и (1)

по гипотенузе и острому углу, т.к рассматриваемые треугольники прямоугольные, .

Т.к. и , отсекая пропорциональные отрезки, то ||.

Известно, что , , поэтому, подставив данные в (1), получим ,

Глава 3. Анкетирование учащихся

Всем ученикам 10 и 11 классов я задала по 4 вопроса:

Знаете ли вы об ортоцентрических треугольниках?

Применяли ли вы свойства ортоцентрических треугольников при решении задач?

Как вы считаете, можно ли облегчить решение задач, используя эти свойства?

Хотели бы вы научиться решать задачи на применение свойств ортоцентрических треугольников?

Подсчитав ответы «да», я получила следующие результаты:

Источник