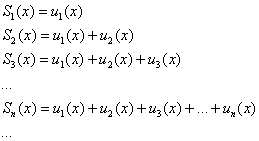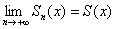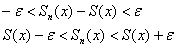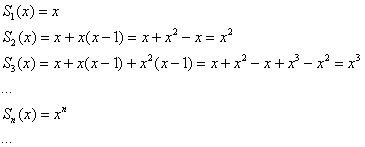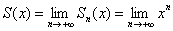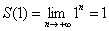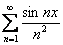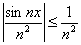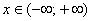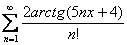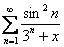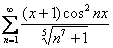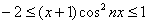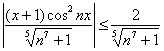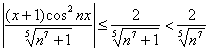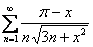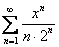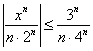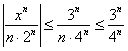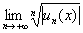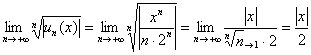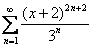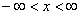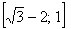Что значит что ряд сходится равномерно

Равномерная сходимость функционального ряда

Содержание

Поточечная сходимость [ править ]

То, как была определена сумма функционального ряда, не учитывает то, что функция — закон соответствия, который каждому [math]x \in E[/math] сопоставляет некоторое число. При этом, все [math]x[/math] фигурировали изолированно.

Пусть на [math]E[/math] [math]f_n[/math] обладает свойством [math]P[/math] (например, непрерывность на [math]E[/math] ). И пусть для любого [math] x \in E [/math] есть предел соответствующей числовой последовательности. Возникает вопрос: «Будет ли [math]f = \lim\limits_ f_n[/math] обладать свойством [math]P[/math] ?»

Приведем пример, показывающий, что если требовать лишь поточечной сходимости, то для [math] f [/math] свойство [math]P[/math] может отсутствовать.

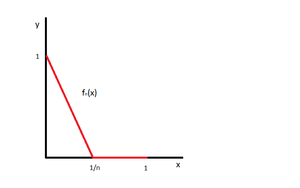
Все [math]f_n[/math] непрерывны на [math][0; 1][/math] . [math]f_n(0) = 1 \to 1[/math] , [math]f(0) = 1[/math] .

[math]0 \lt x \leq 1[/math] : [math]\frac1n \to 0[/math] . Тогда, начиная с некоторого [math]N[/math] , все [math]\frac1N \lt x \Rightarrow f_n(x) = 0[/math]

Тогда [math]f[/math] будет разрывна в нуле, свойство непрерывности не сохранилось.

Равномерная сходимость [ править ]

Возникает вопрос: «Что ещё надо потребовать от поточечной сходимости, чтобы в пределе [math]P[/math] сохранилось?»

Классическое требование: равномерная сходимость.

Определение:

[math]f_1, f_2, \ldots[/math] равномерно сходится к [math]f(x)[/math] , если [math]\forall \varepsilon\ \gt 0\ \exists N\ \forall n \gt N\ \forall x \in E : |f_n(x) — f(x)| \lt \varepsilon[/math] Пишут, что [math]f_n \rightrightarrows f[/math] .

Определение:

Пусть на [math]E[/math] задан функциональный ряд [math]\sum\limits_^\infty f_n[/math] . Тогда он равномерно сходится к [math]f = \sum f_n[/math] , если [math]\forall\varepsilon\ \gt 0\ \exists N\ \forall n \gt N\ \forall x \in E : |S_n(x) — f(x)| \lt \varepsilon[/math]

Далее всё будем писать на языке функциональных рядов, так как их наиболее удобно использовать в математическом анализе, и вообще это очень круто и популярно.

Критерий Коши равномерной сходимости [ править ]

Теорема (Критерий Коши равномерной сходимости):

Доказательство:

[math]\triangleright[/math]

[math]\Longrightarrow[/math] Пусть ряд равномерно сходится. [math]\sum\limits_^m f_k = S_m — S_[/math] [math]\left|\sum\limits_^m f_k \right| = |(S_m — S) + (S — S_)|[/math] , где [math]S[/math] — сумма ряда. Тогда [math]\left|\sum\limits_^m f_k(x)\right| \leq |S_m — S| + |S_ — S|[/math] По определению равномерной сходимости, [math]\forall \varepsilon\ \exists N\ \forall p \gt N\ \forall x \in E : |S_p(x) — S(x)| \lt \varepsilon[/math] . [math]m, n — 1 \gt N [/math] В силу предыдущего неравенства, [math]\forall x \in E : \left|\sum\limits_^m f_k(x)\right| \leq 2\varepsilon[/math] , то есть, выполняется условие критерия Коши. [math]\Longleftarrow[/math] Пусть выполняется условие критерия Коши. [math]\forall x \in E[/math] для [math]\sum\limits_^\infty f_n(x)[/math] выполняется критерий Коши сходимости числовых рядов. Значит, этот ряд сходится. На всем [math]E[/math] определена его сумма. Осталось установить равномерную сходимость ряда. По условию критерия Коши, [math]\forall m \geq n \gt N\ \forall x \in E : \left|\sum\limits_^m f_k(x) \right| \leq \varepsilon[/math] Как и в первой половине доказательства, [math]|S_m(x) — S_(x)| \leq \varepsilon[/math] , но [math]S_p(x) \to S(x)[/math] . В неравенстве с [math]\varepsilon[/math] можно подставлять любой фиксированный [math]x[/math] . Устремим [math]m \to \infty[/math] : [math]\forall n \gt N\ \forall x \in E : |S_n(x) — S(x)| \leq \varepsilon[/math] Значит, определение равномерной сходимости проверено.

[math]\triangleleft[/math]

Признак Вейерштрасса [ править ]

Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса)

Можно рассматривать [math]\sum\limits_^\infty |f_n|[/math] и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.

Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.

Теорема (Вейерштрасс):

Доказательство:

[math]\triangleright[/math]

Применим критерий Коши: [math]\left|\sum\limits_^m f_k(x) \right|[/math] [math]\leq \sum\limits_^m |f_k(x)|[/math] [math]\leq \sum\limits_^m a_k[/math] [math]\sum\limits_^m a_k \lt +\infty \Rightarrow \forall\varepsilon\ \gt 0\ \exists N\ \forall m \geq n \gt N : \sum\limits_^m a_k \lt \varepsilon[/math] Сопоставляя с предыдущим неравенством, которое верно [math]\forall x[/math] , [math]\left|\sum\limits_^m f_k(x)\right| \lt \varepsilon[/math] . Тогда, по критерию Коши, ряд равномерно сходится.

[math]\triangleleft[/math]

Признак Абеля-Дирихле [ править ]

1)Частичные суммы [math] S_k(x)= \sum\limits_^k a_n(x) [/math] ряда [math]\sum\limits_^\infty a_n(x) [/math] равномерно ограничены на [math]E[/math] ;

2)Последовательность функций [math]b_n(x)[/math] монотонна и равномерно сходится к нулю на [math]E[/math] .

Доказательство: [math]\triangleright[/math]

Монотонность последовательности [math]b_n(x)[/math] позволяет при каждом [math]x \in E[/math] записать оценку:

[math] |\sum\limits_^m a_k(x) b_k(x)| \leq 4 max |A_k(x)| * max( |b_n(x)|, |b_m(x)| )[/math]

где [math] n — 1 \leq k \leq m [/math] и в качестве [math] A_k(x)[/math] возьмем [math] S_k(x) — S_(x) [/math] .

Источник

Равномерная сходимость ряда

На уроке о разложении функций в степенные ряды я рассказал вам о самом понятии сходимости ряда и сейчас настал момент познакомиться с важнейшим свойством сходящихся функциональных рядов, а именно с равномерностью сходимости. Ничего сложного в этом нет, как обычно – немного теории и обильная практика. Впрочем, «чайникам» таки лучше начать с первой статьи по теме (ссылка выше), а может быть и вообще с числовых рядов.

Сначала немного освежим воспоминания. Рассмотрим функциональный ряд
и предположим, что данный ряд сходится к функции на некотором промежутке (интервале, полуинтервале или каком-то другом). Что значит «сходится»?

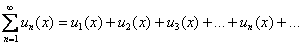
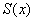
Распишем стройную шеренгу частичных сумм. По сути дела – это тоже «обычные» функции:

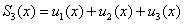
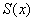
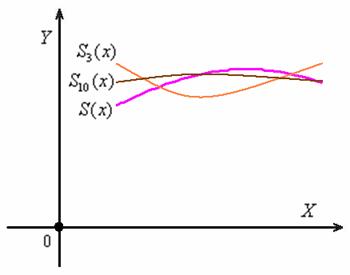
Если мы возьмём, например, функцию, состоящую из первых трёх членов ряда , то её график (в общем случае) будет мало напоминать график функции :

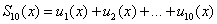
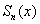
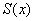
Если рассмотреть функцию из первых 10 членов ряда , то приближение будет уже лучше. И чем больше членов ряда взять – тем ближе график приблизится к графику . Ну а в пределе, не нужно быть провидцем:

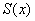
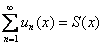
Функция называется суммой функционального ряда: , и как видите, определяется она по тому же принципу, что и сумма ряда числового – через предел частичной суммы.

При этом ещё раз подчёркиваю, что все события происходят в некотором промежутке сходимости ряда. Ибо если при каких-то значениях «икс» функциональный ряд 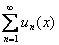расходится, то ни о какой сумме речи быть не может.

Казалось бы, всё просто как пять копеек, однако не тут-то было. Во многих задачах важнА не только сама по себе сходимость, но ещё и её характер суровый, нордический. А сходиться ряд к своей сумме может по-разному: равномерно и неравномерно. Эти термины имеют самый что ни на есть человеческий смысл, в котором мы разберёмся буквально на ближайшем экране. 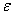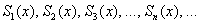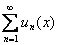И коль скоро, жизнь довела вас до равномерной сходимости ряда, то объяснять я буду строго – с помощью -окрестности =) Выкладки будут весьма похожи на определение предела числовой последовательности. Что не удивительно – ведь сейчас мы тоже изучаем последовательность, только функциональную: – частичных сумм ряда в его промежутке сходимости.

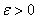
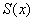
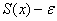
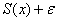
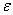
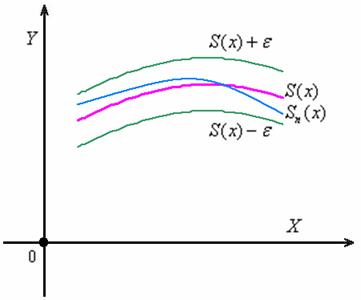
Рассмотрим произвольное значение , которое может быть сколь угодно малым, и заключим сумму ряда в своеобразный «коридор» из двух функций: и . Это и есть -окрестность суммы:

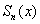
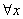
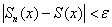
Пусть некоторое приближение (синий цвет) ПОЛНОСТЬЮ лежит внутри «коридора». Аналитически это запишется следующим образом: (для любого «икс») из промежутка сходимости выполнено неравенство . На всякий случай «распакую» модуль для сомневающихся:

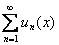
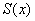
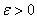
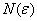
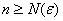
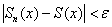
Говорят, что ряд сходится равномерно к функции на некотором промежутке, если для любого значения (заранее выбранного и сколь угодно малого) и СРАЗУ ДЛЯ ВСЕХ «икс» из данного промежутка найдётся натуральный номер (зависящий от «эпсилон»), ТАКОЙ, что для всех номеров будет выполнено неравенство .

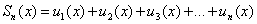
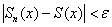
Иными словами, равномерная сходимость подразумевает тот факт, что какой бы мизерный «коридор» мы ни рассмотрели – всегда найдётся частичная сумма , график которой ПОЛНОСТЬЮ окажется внутри «коридора», т.е. будет отличаться от точной суммы по модулю меньше, чем на «эпсилон»:
– для ВСЕХ «икс» из промежутка сходимости.
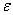
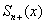
И, разумеется, внутри -окрестности также окажутся все приближения более высоких порядков

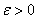
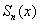
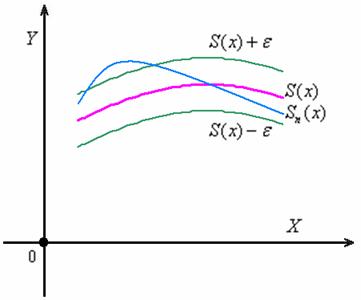
Изложенное свойство выглядит совершенно естественным, но впечатление это обманчиво. Функциональный ряд может сходиться к своей сумме и неравномерно. В этом случае найдётся такое значение (нередко достаточно большое), для которого не существует приближения , которое бы ЦЕЛИКОМ лежало в коридоре. И здесь типично появление «волны»:

С неограниченным увеличением график «синего» приближения будет бесконечно близко приближаться к своей сумме , однако ж «волна» никуда не денется – она будет перемещаться справа налево (например) и бесконечно истончаться, но так и останется ВЫШЕ графика «моря» .

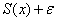
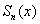
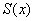
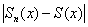
Собственно, в этом и проявляется неравномерность сходимости – даже при ОЧЕНЬ больших значениях «эн» график уж практически везде сольётся с графиком , да всё-таки не везде – найдётся малюсенький участок промежутка сходимости, где расхождение будет больше, чем «эпсилон».

Следует отметить, что с геометрической точки зрения неравномерность может проявляться не только «волной». Разберём хрестоматийный пример, который встречается практически в любом учебнике – не могу удержаться, поскольку нагляднее пример найти трудно:

Рассмотрим функциональный ряд 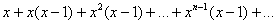и составим последовательность его частичных сумм:

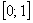
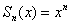
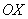
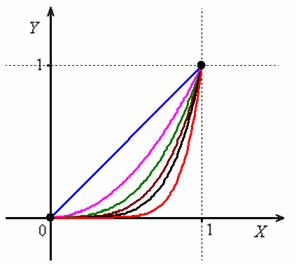
…Эх, где ж мои 12 лет? =) В ходе изучения математики, наверное, многие подметили, что на отрезке с увеличением степени график всё ближе и ближе прижимается к оси :

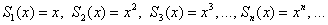
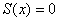
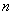
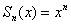
Таким образом, логично предположить, что последовательность частичных сумм сходится к нулевой функции на данном промежутке, причём из чертежа явственно виден неравномерный характер этой сходимости – даже при ОЧЕНЬ больших значениях найдётся наноскопический участок, где график окажется «подвешен» к верхней точке, в то время как львиная его часть будет уже «на дне».

Установим факт сходимости аналитически:

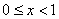
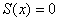
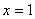
И здесь обнаруживается довольно таки интересная вещь: если , то суммой функционального ряда действительно является ось абсцисс , однако при :

Вот так вот рвутся шаблоны! – несмотря на то, что все члены последовательности 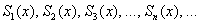непрерывны, её предел терпит разрыв:

И такая ситуация возможна только при НЕравномерной сходимости ряда! Кстати, доказывается неравномерность в данном примере элементарно – берём любую окрестность и опровергаем определение равномерной сходимости.

Какой можно привести пример равномерно сходящегося ряда? В статье о разложениях функций в степенные ряды в качестве подопытного образца я начал мучить ряд 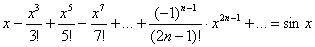и сейчас исследование получает своё продолжение, поскольку сходимость тут как раз равномерна.

Рассмотрим достаточно большой отрезок числовой прямой,… да чего тут мелочиться, пожалуйста, поднимите руку вверх и чуть-чуть согните указательный палец. Это будет начало синусоиды. Теперь мысленно продолжите её до Солнца. …ну, может кто-то хочет до Луны или до соседнего дома – без проблем =) …Представили? Отлично! Обозначим данный кусок через .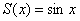

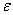
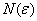
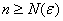
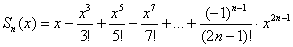
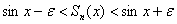
В чём состоит эффект равномерности? Если мы возьмём сколь угодно малую -окрестность этого куска, то для неё найдётся натуральный номер (пусть гигантский), начиная с которого: , график любого приближения ПОЛНОСТЬЮ оказывается внутри заявленного «коридора»: – для ВСЕХ «икс» промежутка – что вблизи вашей руки, что вблизи Солнца, что посередине! СТРОГО внутри, никаких «подвисаний» и тем более «заскоков».

И тот же самый факт справедлив для сколь угодно длинного участка синусоиды (т.к. разложение синуса сходится на всей числовой прямой).

Что можно извлечь полезного из этого примера? …Теперь, когда преподаватель заметит ваш необычный жест или застукает в неловкой позе – вам будет, чем оправдаться! =)

А если серьёзно, то равномерность сходимости приносит нам много плюшек, в частности непрерывность суммы ряда (если частичные суммы непрерывны), а также возможность почленно дифференцировать и интегрировать ряд (с некоторыми дополнительными условиями), чем мы уже активно пользовались на уроке о сумме степенного ряда.

Как доказать равномерность сходимости?

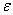
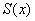
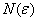
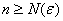
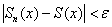
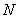
Для некоторых рядов это можно сделать с помощью определения. Алгоритм решения опять же похож на доказательство предела числовой последовательности: для произвольной -окрестности суммы нужно указать натуральный номер – такой, что для любого бОльшего номера и СРАЗУ ДЛЯ ВСЕХ «икс» исследуемого промежутка выполнено неравенство . В случае неравномерно сходящегося ряда такого номера не найдётся, поскольку будет зависеть ещё и от «икс».

Кроме того, существует эквивалентное определение, сформулированное через остаток ряда. Соответствующие примеры можно найти, например, во 2 томе Бохана, но особенно интересно материал изложен у Фихтенгольца (тоже том 2). Ну а я перехожу практической части урока.

На практике в большинстве случаев определение оказывается малопригодным, и поэтому для выявления равномерности обычно пользуются специальными признаками, которые доказаны в теории. Известнейшим, и, пожалуй, единственным признаком, с которым вам придётся реально столкнуться, называется:

Признак равномерной сходимости Вейерштрасса

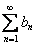
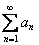
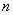
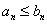
Сначала понятие мажорантного ряда, с которым мы на самом деле уже сталкивались, используя признак сравнения. И понятие как раз удобнее объяснить на числовых рядах: говорят, что ряд мажорирует ряд , если для любого значения выполнено неравенство .

Пример в стиле «меняю рубль на два»:
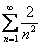
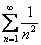
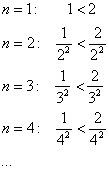
ряд мажорирует ряд . Как самый настоящий мажор:

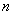
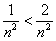
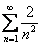
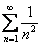
Таким образом, для всех выполнено неравенство , а значит, ряд является мажорантным по отношению к ряду .

Очень, кстати, хорошо, если вы «набили руку» на упомянутом признаке сравнения, а также прорешали соответствующие ряды повышенной сложности – сейчас будет нечто похожее.

Возвращаемся к функциональному ряду 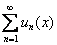и признаку Вейерштрасса:

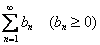
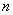
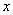
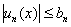
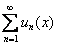
Если существует сходящийся числовой ряд , такой, что для всех и ДЛЯ ВСЕХ из некоторого промежутка выполнено неравенство , то функциональный ряд в данном промежутке сходится, причём равномерно и абсолютно.

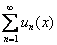
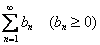
Иными словами, если для функционального ряда на исследуемом промежутке удастся подобрать мажорирующий его числовой ряд , то будет нам счастье.

И, как легко видеть, признак Вейерштрасса пригоден не только для доказательства ИМЕННО равномерности, но и для установления самого факта сходимости! С чего мы и начнём.

Пережили сессию – порвали три баяна:

Найти область сходимости функционального ряда

…как решать? Ведь ряд ни в одном глазу не степенной…. Добавим знаний!

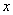
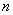
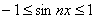
Решение: такой мотив нам тоже встречался – ограниченность синуса. ДЛЯ ЛЮБОГО действительного и для всех выполнены неравенства , поэтому:

Внимание! Если среди членов функционального ряда есть отрицательные, то знак модуля обязателен!

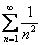
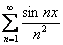
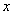
Таким образом, положительный сходящийся ряд мажорирует функциональный ряд на всей числовой прямой, а значит, по признаку Вейерштрасса последний сходится равномерно при любом .

Ответ: область сходимости ряда

Найти область сходимости функционального ряда

Следует отметить, что равномерность сходимости в этих примерах, в общем-то, была «по боку», но условие задачи может быть сформулировано и по-другому: «доказать, что функциональный ряд сходится равномерно на всей числовой прямой». И тогда решение будет отличаться! Постарайтесь справиться самостоятельно:

Доказать, что функциональный ряд сходится равномерно на промежутке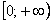

Также обратите внимание ещё на одно отличие: данный ряд, очевидно, сходится и при других значениях «икс», но здесь это не важно – для исследования предложен конкретный промежуток.

Краткие решения в конце урока. И решения действительно краткие. Но со своими тонкостями, и корректно их оформить – не так-то просто, в чём мы очень скоро убедимся.

Чуть усложним типовое задание:

Доказать, что функциональный ряд сходится равномерно на отрезке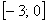

Доказательство: первоначальный анализ показывает, что всё дело нужно свести к сходящемуся мажорантному ряду 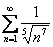(вспоминаем обобщённый гармонический ряд), возможно, с каким-то множителем-константой.

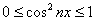
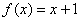
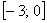
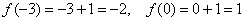
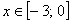
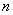
Сначала «подчищаем» числитель. С квадратом косинуса никаких хитростей: , а вот с возрастающей линейной функцией всё интереснее. Вычислим её значения на концах отрезка :

, таким образом, функция возрастает от –2 до 1, а значит, для ЛЮБОГО и для всех номеров значение числителя будет гарантированно находиться в следующих пределах:

И здесь часто допускают машинальную ошибку:
– правильно то оно, формально, правильно. Но совершенно не соответствует признаку Вейерштрасса, в котором речь идёт о модуле: .

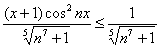
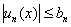
А посему обращаем наш взор на двойное неравенство и делаем вывод о том, что числитель по модулю не превосходит двух!
– ну и что, что мы «прихватили лишнего», это нам совершенно не мешает.

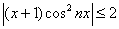
Итак:

Со знаменателем всё проще: так как для любого «эн» выполнено 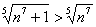, то:

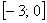
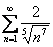
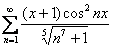
Вывод: на отрезке положительный сходящийся числовой ряд мажорирует функциональный ряд , а значит, по признаку Вейерштрасса он равномерно сходится в данном промежутке. Ч.т.д.

Доказать, что функциональный ряд сходится равномерно на отрезке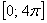

Примерный образец чистового оформления задачи в конце урока.

В моей коллекции есть и более трудные примеры, где требуется выполнить не 2-3, а 4-5 шагов, и некоторые из них напоминают самые настоящие головоломки. Также иногда приходиться предварительно доказать сходимость самого числового ряда (если она не очевидна). Однако я оставлю все эти вещи за кадром и в заключение урока, как водится, десерт:

Равномерная сходимость степенного ряда

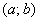
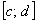
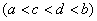
И десерт действительно вкусен: пусть степенной ряд сходится на некотором ненулевом интервале . Тогда его равномерная сходимость гарантирована на любом отрезке , который ПОЛНОСТЬЮ лежит внутри интервала сходимости . Теорема есть такая.

Вопрос равномерной сходимости ряда на концах интервала разберём чуть позже:

Выяснить сходится ли ряд равномерно на промежутке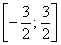

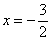
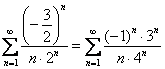
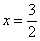
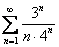
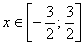
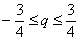
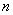
Решение: а почему бы не использовать признак Вейерштрасса? Если , то получаем следующий числовой ряд: , если , то . Очевидно, что при подстановке значений основание получаемой степени будет меняться в пределах , а значит, на данном отрезке для всех справедливо:

и, с помощью неравенства 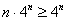совсем упрощаем ситуацию:

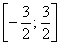
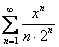
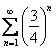
Таким образом, в промежутке функциональный ряд мажорируется бесконечно убывающей геометрической прогрессией и равномерная сходимость установлена.

Можно ли так решать? Конечно. Но далеко не у всех есть хороший навык оценки рядов, и поэтому здесь гораздо проще использовать теорему равномерной сходимости степенного ряда. Кстати, эту возможность нужно еще заметить – условие-то хитро замалчивает, что ряд степенной.

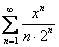
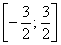
И не зря, ибо решение становится не то что простым, а примитивным: находим интервал сходимости ряда и если отрезок попадает внутрь интервала, то ответ положительный.

Но признак Даламбера мы использовать не будем. На первом уроке по теме я обещал разобрать аналогичный метод, основанный на радикальном признаке Коши, и сейчас настал удачный момент сдержать своё обещание. Алгоритм очень похож – составляем и решаем следующий предел:

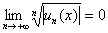
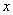
Если окажется, что , то ряд сходится при любом ;
если 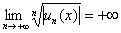, то в единственной точке;
и если предел равен конечному положительному числу, то читаем дальше:

Используя доказанный в курсе математического анализа предел 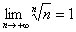, вычислим:

А дальше всё, как «по Даламберу», ряд сходится при: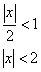

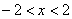
– интервал сходимости степенного ряда.

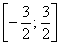
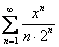
И поскольку отрезок полностью лежит внутри интервала сходимости, то по соответствующей теореме ряд сходится равномерно на данном отрезке.

Ответ: да

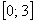
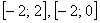
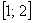
И сейчас небольшое исследование концов интервала. Если предложенный в условии отрезок не входит или «вылезает» за пределы интервала сходимости, например, отрезок , то всё понятно. Но что делать, если нам предложены «пограничные» промежутки: или ?

В этом случае нужно исследовать сходимость степенного ряда на концах интервала:

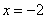
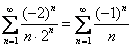
если , то – сходится условно;
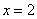
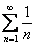
если , то – расходится (гармонический ряд).

Таким образом, область сходимости ряда: 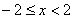. На левом конце сходимость лишь условная, но в плане равномерной сходимости нас устроит и такая!

А теперь раздача рыжих котов:

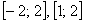
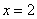
– для отрезков можно дать следующий ответ: «нет, так как в точке ряд расходится»;
– на полуинтервалах 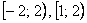ряд сходится неравномерно, т.е. для положительного результата мы не имеем права даже «прикасаться» к точке расходимости!
– и, наконец, положительный ответ: на отрезке 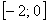ряд сходится равномерно.

На этот счёт тоже существуют свои теоремы, с которыми можно ознакомиться у того же Фихтенгольца.

И перед тем, как подвести итоги, аналогичный пример для самостоятельного решения:

Исследовать ряд на равномерную сходимость на отрезке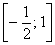

Подумайте, как грамотно ответить на поставленный вопрос 😉 Он весьма и весьма отличен от предыдущей задачи!

Я очень рад, что вы дочитали статью до конца и мужественно преодолели эту жизненную трудность под названием «равномерная сходимость»! =) Пришло время пересчитать патроны и застрелиться. Итак:

Для исследования ряда на равномерную сходимость:

1) Есть определение равномерной сходимости. Между прочим, рабочий вариант.

2) Если ряд степенной, то во многих случаях удобно использовать теорему о равномерной сходимости степенного ряда (см. Примеры 6,7).

3) Для произвольного функционального ряда почти всегда срабатывает признак Вейерштрасса

И слово «почти» здесь носит не только прикладной, но и теоретический смысл – дело в том, что этот признак является лишь достаточным, однако не необходимым. Иными словами, существует равномерно сходящиеся функциональные ряды, которые «не охватываются» признаком Вейерштрасса. В частности, есть неабсолютно, но равномерно сходящиеся ряды. Впрочем, не будем развивать тему – путь в дебри я уже сегодня показал =)

Но вот тема практическая ещё отнюдь не закрыта! Потому что на практике могут запросто встретиться, например, такие функциональные ряды: . Они НЕ степенные и с признаком Вейерштрасса тоже всё кисло. Как исследовать их сходимость? Данному вопросу посвящён дополнительный урок, который я назвал (во многом условно) Функциональные ряды повышенной сложности – не упустите прекрасную возможность поднять свою квалификацию!

Всё выше, и выше, и выше!

Решения и ответы:

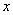
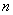
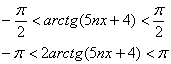
Пример 2: Решение: для всех значений и для всех номеров справедливы неравенства:

Следовательно: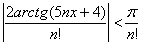

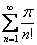
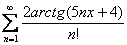
Поскольку положительный ряд сходится (легко проверить по признаку Даламбера), то по признаку Вейерштрасса функциональный ряд равномерно сходится на всей числовой прямой.
Ответ: область сходимости ряда

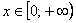
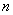
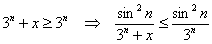
Пример 3: Доказательство: для любого и для всех справедливо неравенство:

Примечание: на рассматриваемом промежутке все члены функционального ряда неотрицательны, и поэтому знак модуля можно опустить.
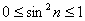
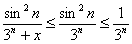
И поскольку , то:

Таким образом, на полуинтервале бесконечно убывающая геометрическая прогрессия мажорирует функциональный ряд , следовательно, по признаку Вейерштрасса он равномерно сходится в данном промежутке. Что и требовалось доказать.

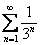
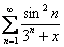
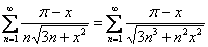
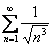
Пример 5: Доказательство: преобразуем общий член ряда: , откуда становится понятно, что в качестве мажорантного ряда следует подбирать сходящийся ряд (возможно с множителем-константой).
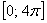
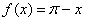
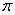
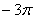
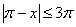
На отрезке функция убывает от до , поэтому: .
Таким образом, для любого :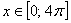

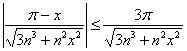
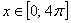
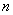
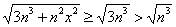
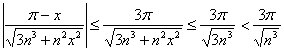
Кроме того, для любого и для всех номеров :
, следовательно:

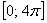
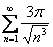
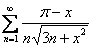
Вывод: на отрезке положительный сходящийся ряд мажорирует ряд , а значит, по признаку Вейерштрасса он равномерно сходится в данном промежутке, ч.т.д.

Пример 7: Решение: данный ряд является степенным. С помощью радикального признака Коши найдём интервал сходимости ряда: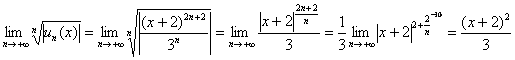

Ряд сходится при: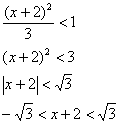

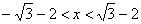
– интервал сходимости степенного ряда.
Отрезок 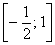выходит за его пределы.
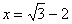
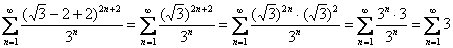
Исследуем сходимость ряда на правом конце интервала – если , то:
– расходится.
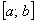
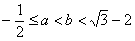
Ответ: ряд сходится равномерно на любом отрезке , где , и расходится на отрезке

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник