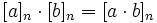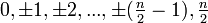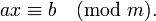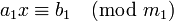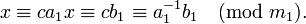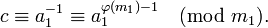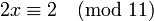- Сравнение по модулю натурального числа
- Сравнение по модулю натурального числа
- Содержание
- Определения
- Свойства равенства по модулю
- Связанные определения
- Классы вычетов
- Системы вычетов
- Решение сравнений
- Сравнения первой степени
- Пример
- Сравнения второй степени
- История
- Сравнения, система вычетов, решение линейных систем по модулю
- Содержание
- Сравнения по модулю [ править ]
- Арифметика сравнений [ править ]
- Свойства сравнений [ править ]
- Полная и приведенная система вычетов [ править ]
- Решение линейных систем по модулю [ править ]
- Примеры решения [ править ]
Сравнение по модулю натурального числа
Сравнение по модулю натурального числа
В теории чисел сравнение [уточнить] по модулю натурального числа n — задаваемое означенным числом отношение эквивалентности на множестве целых чисел, связанное с делимостью на него. Факторпространство по этому отношению называется «кольцом вычетов». Совокупность соответствующих тождеств и алгоритмов образует модульную [уточнить] (или модулярную) арифметику.
Содержание
Определения
Два целых числа a и b сравнимы по модулю натурального числа n (или равноостаточны при делении на n ), если при делении на n они дают одинаковые остатки.
Эквивалентные формулировки: a и b сравнимы по модулю n , если их разность a — b делится на n , или если a может быть представлено в виде a = b + kn , где k — некоторое целое число. Например: 32 и −10 сравнимы по модулю 7, так как
Утверждение « a и b сравнимы по модулю n » записывается в виде:
Свойства равенства по модулю
Отношение сравнения по модулю обладает свойствами
- рефлексивности: для любого целого a справедливо
- симметричности: если
то
- транзитивности: если
и
то
Любые два целых числа a и b сравнимы по модулю 1.
Для того, чтобы числа a и b были сравнимы по модулю n, необходимо и достаточно, чтобы их разность делилась на n.
Если числа 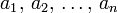
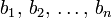
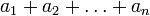
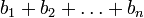
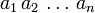
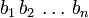
Если числа a и b сравнимы по модулю n, то их степени a k и b k тоже сравнимы по модулю n при любом натуральном k.
Если числа a и b сравнимы по модулю n, и n делится на m, то a и b сравнимы по модулю m.
Для того, чтобы числа a и b были сравнимы по модулю n, представленному в виде его канонического разложения на простые сомножители pi
необходимо и достаточно, чтобы
Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если
Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: 
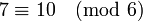
- Можно делить обе части сравнения на число, взаимно простое с модулем: если
и НОД
, то
.
- Можно одновременно разделить обе части сравнения и модуль на их общий делитель: если
, то
.
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.
- Если
и
, то
, где m = [m1,m2] .
Связанные определения
Классы вычетов
Множество всех чисел, сравнимых с a по модулю n называется классом вычетов a по модулю n , и обычно обозначается [a]n или 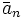
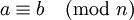
Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел 
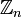
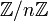
Операции сложения и умножения на 
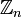
[a]n + [b]n = [a + b]n
Относительно этих операций множество 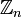
Системы вычетов
Система вычетов позволяет осуществлять арифметические операции над конечным набором чисел, не выходя за его пределы. Полная система вычетов по модулю n ― любой набор из n несравнимых между собой по модулю n целых чисел. Обычно в качестве полной системы вычетов по модулю n берутся наименьшие неотрицательные вычеты
или абсолютно наименьшие вычеты, состоящие из чисел
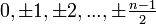
в случае нечётного n и чисел
в случае чётного n .
Набор несравнимых чисел, взаимно простых с n , называется приведённой системой вычетов, см. Мультипликативная группа кольца вычетов.
Решение сравнений
Сравнения первой степени
В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:
Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:
- Если b не кратно d , то у сравнения нет решений.
- Если b кратно d , то у сравнения существует единственное решение по модулю m / d , или, что то же самое, d решений по модулю m . В этом случае в результате сокращения исходного сравнения на d получается сравнение:
где a1 = a / d , b1 = b / d и m1 = m / d являются целыми числами, причем a1 и m1 взаимно просты. Поэтому число a1 можно обратить по модулю m1 , то есть найти такое число c, что 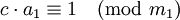
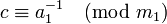
Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
Пример
Для сравнения 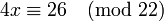
Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: 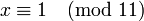
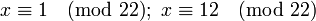
Сравнения второй степени
Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.
История
Китайская теорема об остатках, известная уже много столетий, утверждает (на современном математическом языке), что кольцо вычетов по модулю произведения нескольких взаимно простых чисел является прямым произведением соответственных множителям колец вычетов.
В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.
Источник
Сравнения, система вычетов, решение линейных систем по модулю
Содержание
Сравнения по модулю [ править ]
Будем рассматривать целые числа в связи с остатками от деления их на данное целое число m, которое назовем модулем. Каждому целому числу отвечает определенный остаток от деления его на m. Если двум целым a и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.
Сравнимость для a и b записывается так :
[math]a \equiv b(mod \text < >m)[/math]
Сравнимость чисел a и b по модулю m равносильна:
- а. Возможности представить a в форме [math]\Huge[/math] , где t — целое.
- б. Делимости [math]\Huge[/math] на m.
- Действительно, из [math] a \equiv b(mod \text < >m) [/math] следует [math] a = mq + r, \text < >b = mq_1 + r [/math] , откуда [math] a — b = m(q-q_1)[/math] , и [math] a = b + mt[/math] , где [math] t = q — q_1[/math] .
- Обратно, из [math]\Huge[/math] , представляя b в форме [math] b = mq_1 + r [/math] , выводим [math] a = mq + r [/math] , где [math] q = q_1 + t [/math] , значит [math] a \equiv b(mod \text < >m) [/math] .
Арифметика сравнений [ править ]
Свойства сравнений [ править ]
- 1. Два числа, сравнимые с третьим сравнимы между собой. [math]a \equiv c(mod \text< >m) \text <, >b \equiv c(mod \text< >m) \Rightarrow a \equiv b(mod \text< >m)[/math]
- Легко выводится из пункта «а».
- 2. Сравнения можно почленно складывать. [math] a_1 + a_2 + a_3 \equiv b_1 + b_2 + b_3(mod \text< >m)[/math]
- Представляем сравнения, как в пункте «а» и складываем.
- 3. Сравнения можно почленно перемножать. [math] a_1a_2a_3 \equiv b_1b_2b_3(mod \text< >m)[/math]
- Представляем сравнения, как в пункте «а», перемножаем, получим [math] a_1a_2a_3 = b_1b_2b_3+mN[/math] , где N—целое.
- 4. Обе части сравнения можно разделить на их общий делитель, если последний взаимно прост с модулем.
- Действительно, из [math]a \equiv b(mod \text < >m)[/math] , [math] a = a_1d, b = b_1d, (d,m)=1[/math] следует, что [math] a-b = (a_1 — b_1)d \vdots m [/math] , поэтому [math] a_1 \equiv b_1(mod \text < >m)[/math] .
- 5. Обе части сравнения можно умножить на одно и тоже число.
- Действительно, из [math]a \equiv b(mod \text < >m)[/math] , следует [math] a = b+mt, ak =bk +mkt [/math] , и, следовательно, [math]ak \equiv bk(mod \text < >mk)[/math] .
- 6. Обе части сравнения и модуль можно разделить на их общий делитель.
- Действительно, пусть [math]a \equiv b(mod \text < >m), a = a_1d, b=b_1d, m=m_1d[/math] , отсюда [math] a= b+mt, a_1d =b_1d +m_1dt, a_1 =b_1 +m_1t[/math] , и, следовательно, [math]a_1 \equiv b_1(mod \text < >m_1)[/math] .
- 7. Если сравнение [math]a\equiv b[/math] имеет место по нескольким модулям, то оно имеет место и по модулю равному НОК этих модулей.
- В самом деле, из [math] a \equiv b(mod \text< >m_1),\ldots,a \equiv b(mod \text< >m_k)[/math] следует, что разность [math] a-b [/math] делится на все модули [math] m_1,m_2,\ldots,m_k[/math] . Поэтому она должна делиться и на их НОК.
- 8. Если сравнение имеет место по модулю m, то оно имеет место и по модулю d, равному любому делителю числа m.
- Следует из пункта «б».
- 9. Если одна часть сравнения и модуль делятся на некоторое число, то и другая сторона сравнения должна делиться на это число.
- Следует из пункта «а».
- 10. Если [math]a \equiv b(mod \text< >m) [/math] , то [math](a,m) = (b,m) [/math] .
- Следует из пункта «а» по свойству НОДа.
Полная и приведенная система вычетов [ править ]
Числа равноостаточные(сравнимые по модулю m) образуют класс чисел по модулю m. Из такого определения следует, что всем числам класса отвечает один остаток r, и мы получим все числа класса, если в форме [math]mt + r [/math] заставим t пробегать все целые числа. Таким образом для каждого значения остатка имеется свой класс чисел.
Любое число класса называется вычетом по модулю m. Вычет получаемый при [math] t = 0[/math] , равный самому остатку r, называется наименьшим неотрицательным вычетом.
Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.
Согласно 10 свойству сравнений, числа одного класса по модулю m имеют одинаковый НОД. Особенно важны классы, содержащие числа, взаимно простые с модулем. Взяв вычет от каждого такого класса, получим приведенную систему вычетов по модулю m.
Решение линейных систем по модулю [ править ]
Примеры решения [ править ]
Пример 1.
[math] 12x \equiv 6(mod \text< >18)[/math]
Найдем НОД [math](12,18)=6 [/math]
Перейдем к новому сравнению [math] 2x \equiv 1(3) [/math]
Легко находится [math] x_0 = 2 [/math]
Тогда ответом будет [math] x_0 =2, x_1 = x_0 — \frac
Пример 2.
[math] 111x \equiv 75(mod \text< >321)[/math]
Найдем НОД [math](111,321)=3 [/math] , 75 кратно 3, значит имеем 3 решения
Перейдем к новому сравнению [math] 37x \equiv 25(107) [/math]
Воспользуемся цепными дробями, в нашем случае [math] n=4, p_
Тогда ответом будет [math] x_0 = 99, x_1 = 206, x_2 = 313 [/math] .
Источник
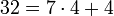
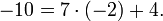
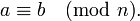
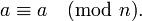
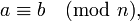 то
то 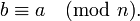
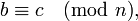 то
то 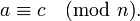
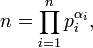
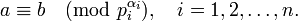

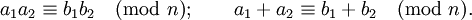
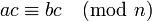 и НОД
и НОД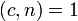 , то
, то 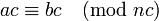 , то
, то 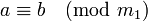 и
и 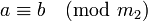 , то
, то 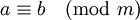 , где m = [m1,m2] .
, где m = [m1,m2] .