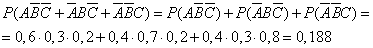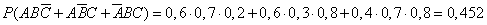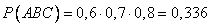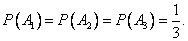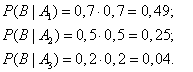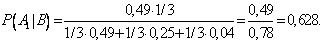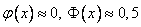Что значит благоприятный исход

Экономический словарь

См. Ситуация риска

Смотреть значение Благоприятный Исход в других словарях

Благоприятный — благоприятная, благоприятное; благоприятен, благоприятна, благоприятно. 1. Способствующий, помогающий чему-н. случай. При благоприятных обстоятельствах. Благоприятная.
Толковый словарь Ушакова

Исход — исхода, м. (книжн.). 1. Движение, выход откуда-н. (устар.). евреев из Египта. 2. Окончание, завершение, результат. Роковой исход дела. В исходе (книжн.) — к концу чего-н. В исходе.
Толковый словарь Ушакова

Благоприятный Прил. — 1. Способствующий, помогающий кому-л., чему-л. 2. Хороший, положительный, приятный. // Содержащий положительную оценку чего-л., согласие с чем-л.
Толковый словарь Ефремовой

Исход М. — 1. устар. Действие по знач. глаг.: исходить (2*1). 2. перен. Способ разрешить затруднения, возможный выход из сложных или неприятных обстоятельств. 3. Окончание, завершение чего-л. // Результат.
Толковый словарь Ефремовой

Благоприятный — -ая, -ое; -тен, -тна, -тно.
1. Способствующий, помогающий чему-л., удобный для чего-л. Б. момент, случай. Работать в благоприятных условиях. Наиболее б. для здоровья климат.
2.
Толковый словарь Кузнецова

Исход — -а; м.
1. к Исходить (2.И.; 1 зн.).
2. Способ разрешить какое-л. затруднение, выйти из сложных обстоятельств. Благополучный и. Найти и. из создавшегося положения. Единственно.
Толковый словарь Кузнецова

Определившийся Исход В Военной Медицине — оценка состояния здоровья военнослужащего после окончания лечения, по официально принятым критериям, отражающим результат лечения и пригодность выписанного пораженного.
Большой медицинский словарь

Исход — («Книга исхода») — вторая книга Пятикнижия.
Большой энциклопедический словарь

Прогноз Болезни Благоприятный — (р. bona) П. б., согласно которому ожидается полное выздоровление или доброкачественное течение болезни.
Большой медицинский словарь

Исход — — вторая книга Пятикнижия Моисеева, составная часть Ветхого Завета, о том, как древние евреи, попавшие в рабство к египетскому фараону, были выведены из Египта по воле.
Исторический словарь

Исход, Книга — -вторая книга Моисеева Пятикнижия (см.) и Библии (см.). Название книге дано 70 переводчиками (в еврейском тексте она называется первыми словами книги: «Эти имена»). Книга.
Исторический словарь

Исход Лечения — (treatment outcome) Наиболее важным вопросом в научном изучении лечения является оценка его эффективности. Трудности, возникающие при проведении таких оценочных исслед.
Психологическая энциклопедия

Определи́вшийся Исхо́д — в военной медицине — оценка состояния здоровья военнослужащего после окончания лечения, по официально принятым критериям, отражающим результат лечения и пригодность.
Медицинская энциклопедия

Исход — — вторая книга Пятикнижия Моисеева, сост. части Ветхого завета. В И. излагается библ. предание о том, как др. евреи, попавшие в рабство к егнп. фараону, были выведены из.
Философский словарь

Исход К Востоку. Предчувствия И Свершения. Утверждение Евразийцев — — сб. статей Н.С. Трубецкого, Савицкого, Флоровского, Сувчинского, вышедший в Софии в 1921 г. Вместе с изданным годом ранее соч. Трубецкого «Европа и человечество» стал первым.
Философский словарь

Красивый, Благоприятный, Годный, Удобный, Настоящий — Философский смысл термина: (О человеке): прекрасный (Гомер, Платон); добродетельный, (Платон, стоики); совестливый (Новый завет).
Философский словарь

БЛАГОПРИЯТНЫЙ — БЛАГОПРИЯТНЫЙ, -ая, -ое; -тен, -тна. Способствующий чему-н., хороший. Благоприятные условия. Б. результат. || сущ. благоприятность, -и, ж.
Толковый словарь Ожегова

ИСХОД — ИСХОД, -а, м. 1. Выход откуда-н. (устар.). Из бездны нет исхода. 2. Завершение, конец. Счастливый и. дела. В исходе (на ис- ходе) дня (вечером). Летальный м. (смерть; спец.). Ладейныйи.
Толковый словарь Ожегова

Источник

Значение словосочетания «благополучный исход»

Значение слова «благополучный&raquo

БЛАГОПОЛУ́ЧНЫЙ , —ая, —ое; —чен, —чна, —чно. Сопровождаемый успехом, удачный, Благополучный исход. Благополучная развязка. (Малый академический словарь, МАС)

Значение слова «исход&raquo

ИСХО́Д , -а, м. 1. Книжн. устар. Действие по глаг. исходить 2 (в 1 знач.). (Малый академический словарь, МАС)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: хук — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «благополучный&raquo

Ассоциации к слову «исход&raquo

Синонимы к словосочетанию «благополучный исход&raquo

Предложения со словосочетанием «благополучный исход&raquo

• При этом планировалось, что аппарат будет управляемым и маневрирующим, что повышало шансы благополучного исхода дела.

Цитаты из русской классики со словосочетанием «благополучный исход»

• За моими плечами было около девяноста процентов за благополучный исход .

Сочетаемость слова «благополучный&raquo

Сочетаемость слова «исход&raquo

Понятия, связанные со словосочетанием «благополучный исход»

Афоризмы русских писателей со словом «благополучный&raquo

• Благополучны те народы,
  Которы красотам природы
  Искусством могут подражать.

Отправить комментарий

Дополнительно

Значение слова «благополучный&raquo

БЛАГОПОЛУ́ЧНЫЙ , —ая, —ое; —чен, —чна, —чно. Сопровождаемый успехом, удачный, Благополучный исход. Благополучная развязка.

Значение слова «исход&raquo

ИСХО́Д , -а, м. 1. Книжн. устар. Действие по глаг. исходить 2 (в 1 знач.).

Предложения со словосочетанием «благополучный исход&raquo

При этом планировалось, что аппарат будет управляемым и маневрирующим, что повышало шансы благополучного исхода дела.

Операции ждать придётся довольно долго, ну и вообще… вероятность благополучного исхода невелика.

После такого наглядного опыта и слухов о всё усиливающейся пропаганде надежда на благополучный исход войны и вера в целесообразность моей миссии у меня подрывалась.

Источник

Благоприятный Исход

Словарь бизнес-терминов. Академик.ру . 2001 .

Смотреть что такое «Благоприятный Исход» в других словарях:

надеясь на благоприятный исход — нареч, кол во синонимов: 1 • наудачу (26) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

получивший благоприятный исход — прил., кол во синонимов: 1 • решившийся (67) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

благоприятный — ▲ хороший ↑ для (чего) < > неблагоприятный благоприятный положительный для чего л. (# условия). благой (# вести). утешительный (# известие). ▼ позитивный ↓ польза … Идеографический словарь русского языка

неблагоприятный исход — проигрыш. Ant. благоприятный исход, выигрыш Словарь русских синонимов. неблагоприятный исход сущ., кол во синонимов: 1 • неудовлетворительный исход … Словарь синонимов

неблагоприятный исход — Syn: проигрыш Ant: благоприятный исход, выигрыш … Тезаурус русской деловой лексики

МЕНИНГИТЫ — МЕНИНГИТЫ. Содержание: Этиология. 799 Менинтеальиый симптомокомплеке. 801 Серозные М. 805 Гнойные М. 811 Эпидемический перебро спинальйый М. . . . . 814 Туберкулезный… … Большая медицинская энциклопедия

Иллюзия контроля — Иллюзия контроля одно из когнитивных искажений, выражающееся в тенденции людей верить в то, что они каким либо образом могут влиять на события, которые на самом деле от них не зависят или зависят в гораздо меньшей степени. Эффект… … Википедия

Пищевод — I Пищевод (esophagus) отдел пищеварительного тракта, соединяющий глотку с желудком. Принимает участие в проглатывании пищи, перистальтические сокращения мышц П. обеспечивают продвижение пищи в желудок. Длина П. взрослого человека равна 23 30 см,… … Медицинская энциклопедия

МАЛЯРИЯ — МАЛЯРИЯ, от итальянского malaria испорченный воздух, перемежная, перемежающаяся, болотная лихорадка (malaria, febris intermittens, франц. paludisme). Под этим названием объединяется группа близко стоящих друг к другу родственных б ней,… … Большая медицинская энциклопедия

ПРОЛЕЖНИ — (лат. decubitus), как указывает самое название, представляют трофическое расстройство, располагающееся главным образом на крестце, ягодицах, лопатках, локтях, пятках и отличающееся гангренозными изменениями, значительным распространением по… … Большая медицинская энциклопедия

Источник

Синонимы к словосочетанию «благоприятный исход»

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: информирование — это что-то нейтральное, положительное или отрицательное?

Связанные слова и выражения

Связанные слова (по тематикам)

• Люди: участник, победитель, умирающий, пессимист, враг
• Места: один, пасть, юдоль
• Предметы: том, календарь, яд
• Действия: исход, результат, успех, стечение, обстоятельство
• Абстрактные понятия: прогноз, удача, период, предпосылка, тенденция

Ассоциации к слову «исход&raquo

Предложения со словосочетанием «благоприятный исход&raquo

• Однако в отношении правительницы полусвета, хитрой и проницательной, такое объяснение благоприятного исхода дел не представляется убедительным.

Цитаты из русской классики со словосочетанием «благоприятный исход»

• По правде сказать, Савин уже не надеялся на благоприятный исход их апелляционной жалобы и заранее был уверен, что палата утвердит приговор суда первой инстанции.

Сочетаемость слова «благоприятный&raquo

Сочетаемость слова «исход&raquo

Значение слова «благоприятный&raquo

БЛАГОПРИЯ́ТНЫЙ , —ая, —ое; —тен, —тна, —тно. 1. Способствующий, помогающий чему-л., удобный для чего-л. Благоприятный момент. Благоприятные условия. (Малый академический словарь, МАС)

Значение слова «исход&raquo

ИСХО́Д , -а, м. 1. Книжн. устар. Действие по глаг. исходить 2 (в 1 знач.). (Малый академический словарь, МАС)

Афоризмы русских писателей со словом «благоприятный&raquo

• Храбрые люди выжидают благоприятных случаев — сильные их создают.

Отправить комментарий

Дополнительно

Значение слова «благоприятный&raquo

БЛАГОПРИЯ́ТНЫЙ , —ая, —ое; —тен, —тна, —тно. 1. Способствующий, помогающий чему-л., удобный для чего-л. Благоприятный момент. Благоприятные условия.

Значение слова «исход&raquo

ИСХО́Д , -а, м. 1. Книжн. устар. Действие по глаг. исходить 2 (в 1 знач.).

Предложения со словосочетанием «благоприятный исход&raquo

Однако в отношении правительницы полусвета, хитрой и проницательной, такое объяснение благоприятного исхода дел не представляется убедительным.

Только инсайдеры располагают информацией, которая даёт им на бирже существенную вероятность благоприятного исхода сделки.

Родители были в ужасе, но продолжали цепляться за надежду на более благоприятный исход.

Источник

Теория вероятностей, формулы и примеры

О чем эта статья:

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Дискретная случайная величина — величина, которая в результате испытания может принимать определенные значения с определенной вероятностью, то есть образовывать счетное множество.

Элементы множества можно пронумеровать. Они могут быть как конечными, так и бесконечными. Например: количество выстрелов до первого попадания в цель.

Непрерывная случайная величина — это такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка. Количество возможных значений непрерывной случайной величины бесконечно.

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Вероятностное пространство — это тройка (Ω, Σ, Ρ) иногда обрамленная угловыми скобками: ⟨ , ⟩ , где

• Ω — это множество объектов, которые называют элементарными событиями, исходами или точками.
• Σ — сигма-алгебра подмножеств , называемых случайными событиями;
• Ρ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

• Вероятность достоверного события равна единице.
• Вероятность невозможного события равна нулю.
• Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

• 0 ≤ P(A) ≤ 1.

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

1. A — встреча с другом состоится, х и у — время прихода. Значит:
   0 ≤ х, у ≤ 60.
2. В прямоугольной системе координат этому условию удовлетворяют точки, которые лежат внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть:

x−y y.

Этим неравенствам удовлетворяют точки из области G — то, что выделено красным:

Тогда вероятность встречи равна отношению площадей области G и квадрата:

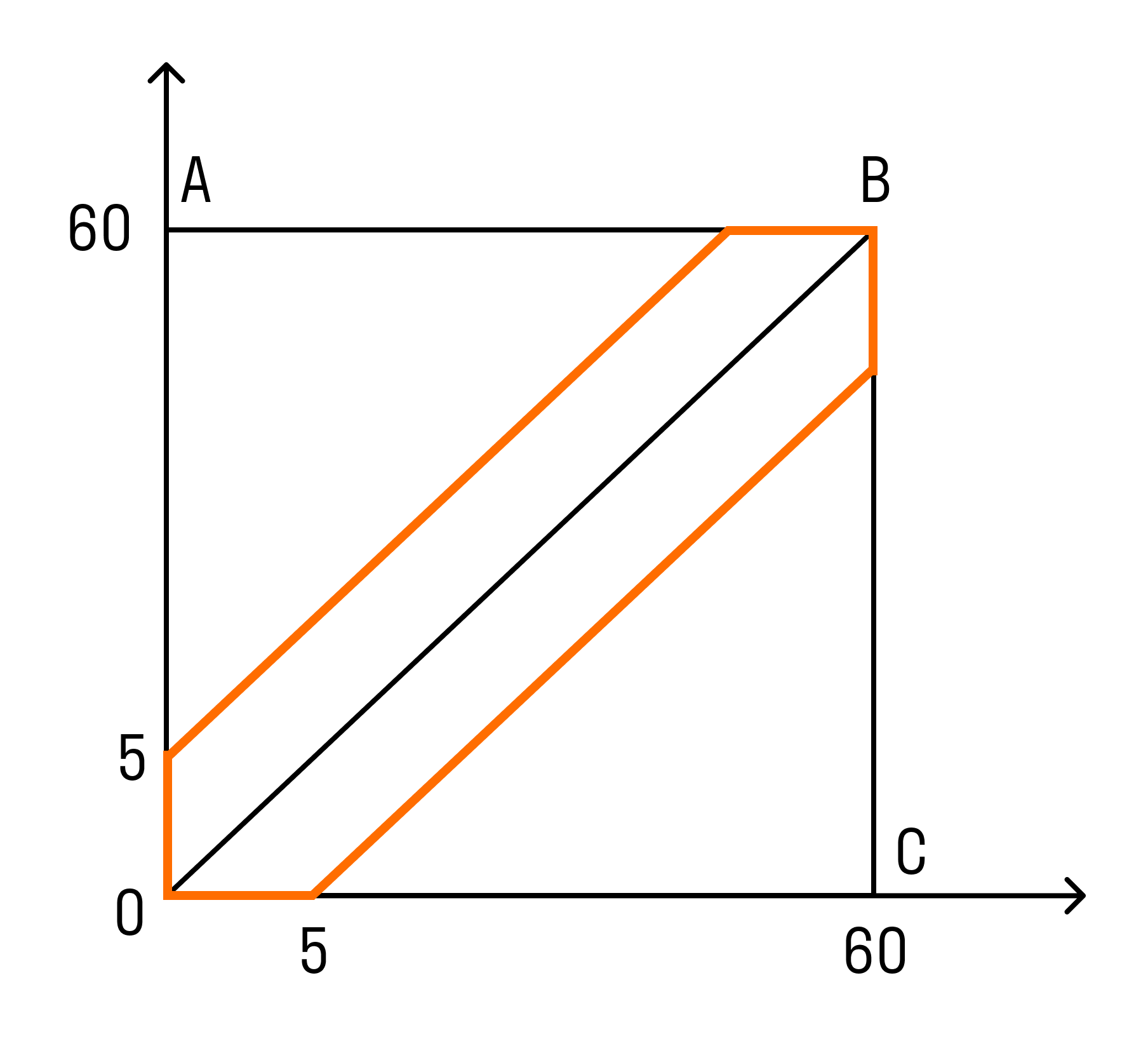
P(A)=S_G/S_OABC= 60 * 60 — 55 * 5560 * 60 = 23144 = 0,16

У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!

Сложение и умножение вероятностей

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

• P(A₁) + P(A₂) + … + P(A_n) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1. 
2. 
3. 

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

Если событие А может произойти только при выполнении одного из событий B₁, B₂, . B_n, которые образуют полную группу несовместных событий — вероятность события А вычисляется по формуле полной вероятности:

Вновь рассмотрим полную группу несовместных событий B₁, B₂, . B_n, вероятности появления которых P(B₁), P(B₂), . P(B_n). Событие А может произойти только вместе с каким-либо из событий B₁, B₂, . B_n, которые называются гипотезами. Тогда по формуле полной вероятности: если событие А произошло — это может изменить вероятности гипотез P(B₁), P(B₂), . P(B_n).

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

1. Возможны три гипотезы:
   • А1 — на линию огня вызван первый стрелок,
   • А2 — на линию огня вызван второй стрелок,
   • А3 — на линию огня вызван третий стрелок.

2. Так как вызов на линию огня любого стрелка равно возможен, то
   
3. В результате опыта наблюдалось событие В — после произведенных выстрелов мишень не поражена. Условные вероятности этого события при наших гипотезах равны:
   
4. По формуле Байеса находим вероятность гипотезы А₁ после опыта:
   

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

• Бросаем игральный кубик, где вероятности выпадения определенной цифры одинаковы в каждом броске.
• Включаем лампы с заранее заданной одинаковой вероятностью выхода из строя каждой.
• Лучник повторяет выстрелы по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Обозначим вероятность появления события А в единичном испытании буквой р, значит:

p = P(A), а вероятность противоположного события (событие А не наступило) — буквой q

q = P(¯A) = 1 — p.

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли:

P_n(k) = C_n k * p k * q n-k , где q = 1 — p.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

np — q ≤ k ≤ np + p, где q=1−p

Так как np−q = np + p−1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np), то есть когда np + p (а отсюда и np — q) нецелое число, либо два значения, когда np — q целое число.

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

1. По условию дано: n = 730, p = 1/365, g = 364/365
2. np — g = 366/365
3. np + p = 731/365
4. 366/365 ≤ m ≤ 731/365
5. m = 2

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

1. По условию дано: n = 1000, p = 0,002, λ = np = 2, k = 3.
2. Искомая вероятность после подстановки в формулу:

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью p, q = 1 — p (условия схемы Бернулли). Обозначим как и раньше, через P_n(k) вероятность ровно k появлений события А в n испытаниях.

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

• 
• при больших x верно

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник