Что значит адиабатный процесс

Адиабатный процесс, его суть и и формулы

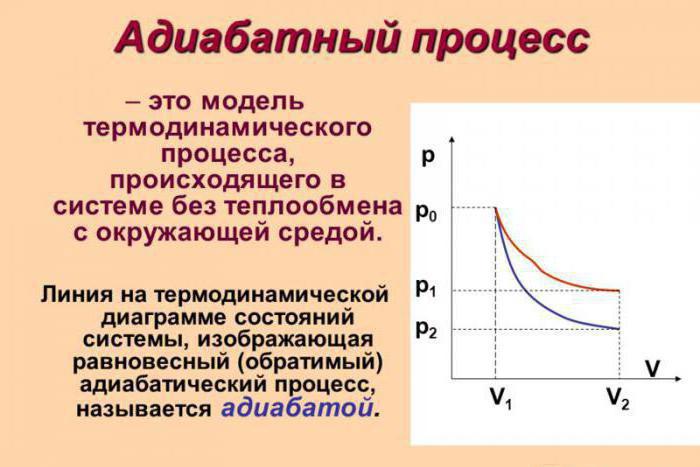
Адиабатный процесс (в некоторых источниках упоминается как адиабатический) — это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.

Связь с первым началом термодинамики

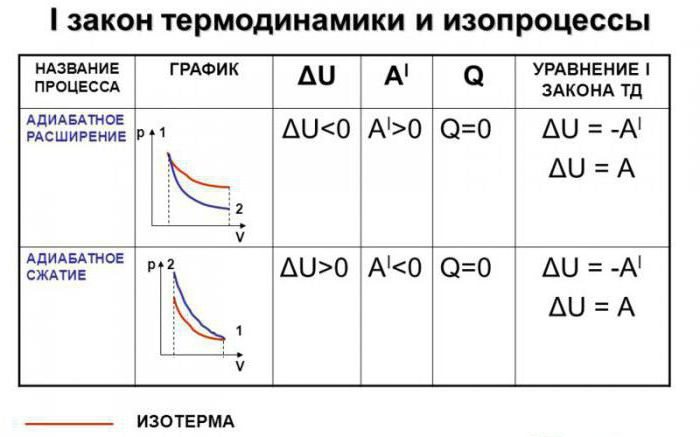
Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.

Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.

В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении. Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю. Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.

Следствие из первого начала термодинамики для адиабатического процесса

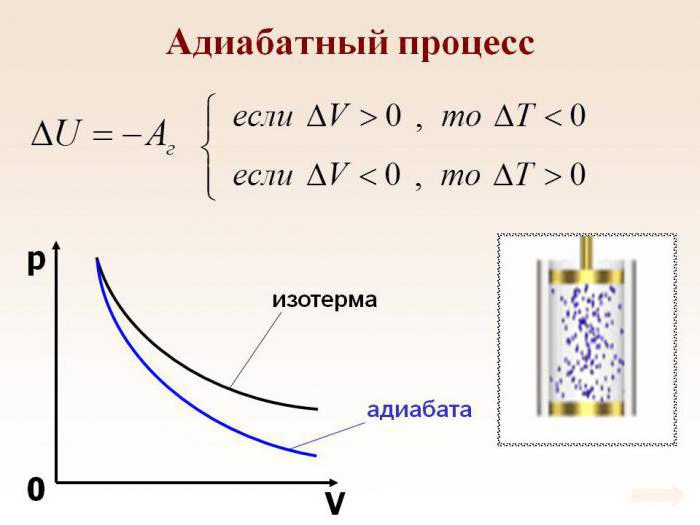
Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.

Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.

Адиабатный процесс. Формулы

Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.

Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = — (интеграл) от dU. Раскроем это выражение, получим: A = — xCv (интеграл в пределах от T1 до T2) dT.

Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = — xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).

Уравнение адиабаты

Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.

В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования. Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения. Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.

Первичное выражение

Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp — Cv)

По сути дела, первая часть задачи выполнена. Остается только довести все до ума.

Вторичное выражение. Подстановка значения

Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.

Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю. Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен. В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.

Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.

Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона. Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.

Примеры адиабатных процессов

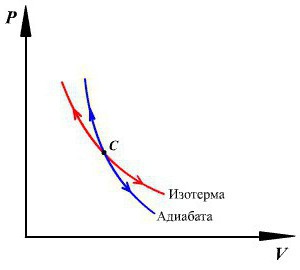
Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.

Заключение

С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике. Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов. Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.

Источник

Адиабатический процесс

Тепловые процессы
Статья является частью одноименной серии.
Адиабатический процесс
Изохорный процесс
Изобарный процесс
Изотермический процесс
Изоэнтропийный процесс
Изоэнтальпийный процесс
Политропный процесс
править
См. также «Физический портал»

Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Серьёзное исследование адиабатических процессов началось в XVIII веке [1] .

Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна [2] . Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы [3] .

Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике.

Содержание

История

Существование атмосферного давления было показано рядом экспериментов в XVII веке. Одним из первых доказательств гипотезы стали магдебургские полушария, сконструированные немецким инженером Герике. Из сферы, образованной полушариями, выкачивался воздух, после чего их было трудно разъединить в силу внешнего давления воздуха. Другой эксперимент в рамках исследования природы атмосферного давления поставил Роберт Бойль. Он состоял в том, что если запаять изогнутую стеклянную трубку с короткого конца, а в длинное колено постоянно подливать ртуть, она не поднимется до верха короткого колена, поскольку воздух в трубке, сжимаясь, будет уравновешивать давление ртути на него. К 1662 году данные опыты позволили прийти к формулировке закона Бойля — Мариотта [4] .

В 1779 году в «Пирометрии» Ламберта был описан опыт повышения и понижения температуры в приёмнике воздушного насоса при движении поршня. Впоследствии данный эффект был подтверждён Дарвином (1788) и Пикте (1798). В 1802 году Дальтон опубликовал доклад, в котором, в числе прочего, указал, что сгущение газов сопровождается выделением тепла, а разрежение — охлаждением. Рабочий оружейного завода зажёг трут в дуле духового ружья путём сжатия воздуха, о чём сообщил в 1803 году лионский физик Моле [1] .

Теоретическим обобщением накопившихся экспериментальных знаний занялся известный физик Пуассон. Так как при адиабатическом процессе температура непостоянна, то закон Бойля — Мариотта требует поправки, которую Пуассон обозначил как коэффициент k и выразил через соотношение теплоёмкостей. Экспериментально данный коэффициент определялся Вальтером и Гей-Люсcаком (эксперимент описан в 1807 году) и затем, более точно Дезормом и Клеманом в 1819 году. Практическое использование адиабатического процесса предложил С. Карно в работе «Движущая сила огня» в 1824 году [1] .

Физический смысл адиабатического процесса

Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии [5] , то адиабатический процесс в силу отсутствия теплообмена () системы со средой сводится только к последним двум процессам [6] . Поэтому, первое начало термодинамики в этом случае приобретает вид [7] [Комм 1]

где — изменение внутренней энергии тела, — работа, совершаемая системой.

Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит [8] :

Работа газа

Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок совершать работу [9] [10]

где F — сила, с которой газ действует на поршень. Перепишем уравнение:

где s — площадь поршня. Тогда работа будет равна [9] [10]

где — давление газа, — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки на которых расширение одинаково [9] .

Основное уравнение термодинамики примет вид [11] :

(1)

Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим [12] [13] .

Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид:

(1a)

где , — дифференциальное выражение для работы, — внешние параметры, которые меняются при совершении работы, — соответствующие им внутренние параметры, которые при совершении малой работы можно считать постоянными. При совершении работы путём сжатия или расширения внутренний параметр — давление. Внешний параметр — объём.

Внутренняя энергия идеального газа

Внутренняя энергия является однозначной функцией состояния системы. Поэтому применительно к адиабатическому процессу её изменение имеет тот же физический смысл, что и в общем случае. Согласно закону Джоуля, выведенному экспериментально, внутренняя энергия идеального газа не зависит от давления или объёма газа. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, [14] . Иными словами — это предельное соотношение изменения внутренней энергии и породившего его изменения температуры. При этом, по определению частной производной считается только то изменение внутренней энергии, которое порождено именно изменением температуры, а не другими сопутствующими процессами. Так как внутренняя энергия идеального газа является функцией только температуры, то

(2)

где — число молей идеального газа.

Уравнение Пуассона для идеального газа

Адиабата Пуассона

Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением [6] [15] [16]

где — его объём, — показатель адиабаты, и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

где — абсолютная температура газа. Или к виду

Поскольку всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении ) газ нагревается ( возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент .

Вывод уравнения

Согласно закону Менделеева — Клапейрона [6] справедливо соотношение

где R — универсальная газовая постоянная. Продифференцировав обе части, получаем

(3)

Если в (3) подставить из (2), а затем из (1), получим

или, введя коэффициент :

.

Это уравнение можно переписать в виде

что после интегрирования даёт уравнение

.

что и требовалось доказать.

Показатель адиабаты

Показатели адиабаты для различных газов [17] [18]
Темп.	Газ	k	Темп.	Газ	k
−181 °C	H2	1.597	20 °C	He	1.660
−76 °C		1.453	20 °C	H2O	1.330
20 °C		1.410	100 °C		1.324
100 °C		1.404	200 °C		1.310
400 °C		1.387	−180 °C	Ar	1.760
1000 °C		1.358	20 °C		1.670
2000 °C		1.318

При адиабатическом процессе показатель адиабаты равен .

Для нерелятивистского невырожденного одноатомного идеального газа [19] , для двухатомного [19] , для трёхатомного , для газов, состоящих из более сложных молекул, показатель адиабаты определяется числом степеней свободы (i) конкретной молекулы, исходя из соотношения .

Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно для низких температур, когда большую роль начинает играть межмолекулярное взаимодействие. Для его теоретического нахождения следует проводить расчёт без некоторых допущений, в частности, использованных при выводе формулы (1) и использовать формулу (1а).

Один из методов для экспериментального определения показателя был предложен в 1819 г. Клеманом и Дезормом. Стеклянный баллон вместимостью несколько литров наполняется исследуемым газом при давлении . Затем открывается кран, газ адиабатически расширяется, и давление падает до атмосферного — . Затем происходит его изохорное нагревание до температуры окружающей среды. Давление повышается до . В результате такого эксперимента k можно вычислить как [20]

Энтропия и обратимость

В общем случае для произвольной физической системы изменение состояния при адиабатическом расширении определяется производными термодинамических параметров при постоянной энтропии. Справедливы соотношения

, ,

где C_p и C_v — теплоёмкости при постоянном давлении и объёме, которые всегда положительны по своему физическому смыслу, — обозначение частной производной. Как и при определении молярной теплоёмкости, при расчёте частной производной находится изменения параметра в числителе, которое происходят только под действием изменения параметра, стоящего в знаменателе. Пусть система адиабатически расширяется, то есть . Тогда если коэффициент теплового расширения положительный, изменение температуры должно быть отрицательным. То есть, температура системы будет уменьшатся при адиабатическом расширении, если коэффициент теплового расширения положителен, и увеличиваться в противоположном случае [21] . Примером подобного процесса является эффект Джоуля — Томсона, который также является необратимым адиабатическим процессом [22] .

Необратимость адиабатических процессов связана с неравновесным переходом от начального состояния к конечному: система не следует адиабате Пуассона , поэтому точный путь системы в координатах термодинамичесих величин не может быть указан. К необратимости может привести наличие внутреннего трения в газе, которое изменит энтропию системы. Так как выделяемое при изменении энтропии тепло не покидает систему (отсутствие обмена теплом с окружающей средой может быть навязано помещением системы в термостат), меняется температура газа. Изменение энтропии необратимого процесса из состояния A в состояние B можно расчитать соединив их на диаграмме несколькими отрезками путей, соответствующих обратимым процессам. Примерами необратимых адиабатических процессов являются дросселирование и смешение двух газов, первоначально находившихся при разных температурах и давлениях внутри поделённого пополам термостата [22] [23] [24] .

Примеры

Открытие адиабатического процесса практически сразу нашло применение в дальнейших исследованиях. Создание теоретической модели цикла Карно позволило установить пределы развития реальных тепловых машин [Комм 3] . Однако, цикл Карно трудно осуществим для некоторых реальных процессов, так как входящие в его состав изотермы требуют определённой скорости теплообмена [25] . Поэтому были разработаны принципы циклов, частично сходных с циклом Карно, например, цикл Отто, цикл сжижения газа, которые были бы применимы в конкретных практических задачах.

Также, дальнейшие исследования показали, что некоторые процессы в природе, например, распространение звука в газе можно с достаточной степенью приближения описывать адиабатическим процессом и выявлять их закономерности [26] . Химическая реакция внутри объёма газа в случае отсутствия теплообмена с окружающей средой также по определению будет адиабатическим процессом. Таким процессом является, например, адиабатическое горение. Для атмосферы Земли также считается адиабатическим процесс совершения газом работы на увеличение его потенциальной энергии. Исходя из этого, можно определить адиабатический градиент температуры для атмосферы Земли [27] . Теория адиабатического процесса употребляется и для других астрономических объектов с атмосферой. В частности, для Солнца наличие макроскопических конвекционных движений теоретически определяют путём сравнения адиабатического градиента и градиента лучевого равновесия [28] .

Цикл Карно

Цикл Карно является идеальным термодинамическим циклом. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно [8] [29] .

Максимальное КПД достигается при обратимом цикле [8] . Для того, чтобы цикл был обратимым, из него должна быть исключена передача тепла при наличии разности температур. Чтобы доказать этот факт, предположим, что передача тепла при разности температур имеет место. Данная передача происходит от более горячего тела к более холодному. Если предположить процесс обратимым, то это означало бы возможность передачи тепла обратно от более холодного тела к более нагретому, что невозможно, следовательно процесс необратим [25] . Соответственно, преобразование тепла в работу может происходить только изотермически [Комм 4] . При этом обратный переход двигателя в начальную точку только путём изотермического процесса невозможен, так как в этом случае вся полученная работа будет затрачена на восстановление исходного положения. Так как выше было показано, что адиабатический процесс может быть обратимым — то этот вид адиабатического процесса подходит для использования в цикле Карно.

Всего при цикле Карно происходят два адиабатических процесса [29] :

1. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс 2→3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
2. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс 4→1). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

Цикл Отто

При идеальном цикле Отто, который приближённо воспроизведён в бензиновом двигателе внутреннего сгорания, второй и третий из четырёх тактов являются адиабатическими процессами [Комм 5] . Работа, которая совершается на выходе двигателя равна разности работ который произведёт газ над поршнем во время третьего такта (т.е рабочего хода), и работы, которую затрачивает поршень на сжатие газа во время второго такта. Так как в цикле Отто используется система принудительного зажигания смеси, то происходит сжатие газа в 7—12 раз [30] .

Рассчитаем пример процесса, происходящего в двигателе внутреннего сгорания при адиабатическом сжатии. Примем величину сжатия 10 и объём двигателя 10 −3 м 3 (1л). Перед сжатием припишем смеси околокомнатную температуру

27 °C или 300 K и нормальное атмосферное давление

100 кПа. Газ смеси будем считать идеальным. Тогда

Рассмотрим процесс сжатие газа до объёма 100 мл. Константа адиабатического сжатия остаётся при этом 6,31. Итого получаем:

что даёт решение для P:

что составляет приблизительно 24,5 атмосферы. Однако в процессе сжатия изменилось не только давление, но и температура газа, которую можно рассчитать по закону Менделеева — Клапейрона:

Теперь, подставляя объём 100 мл и вычисленное нами ранее давление получаем температуру:

Как видно из решения, такая температура, не может привести к самоподжигу топлива [Комм 6] . Выводы из расчёта справедливы и для реальных двигателей, так как в них при данной степени сжатия самоподжига не происходит [30] .

Прохождение волн в газе

Для небольших объёмов газа адиабатическим процессом, близким к обратимому, можно считать процессы в небольших объёмах газа при прохождении звуковой волны [6] .

На основании этого можно расчитать скорость звука в газах путём нахождения зависимости в малом цилиндрическом объёме газа с площадью S и длиной , где x — направление распространения волны, а — смещение точек внутри цилиндра под действием волны. Сопоставив найденное уравнение с волновым уравнением, получим [26] :

где — абсолютная температура в кельвинах; — температура в градусах Цельсия; — молярная масса. По порядку величины скорость звука в газах близка к средней скорости теплового движения молекул и в приближении постоянства показателя адиабаты пропорциональна квадратному корню из абсолютной температуры. Данные выражения являются приближённым, поскольку основываются на уравнениях, описывающих поведение идеального газа. При больших давлениях и температурах необходимо вносить соответствующие поправки, в частности, точно вычислить соотношение для невозмущённого волной газа [26] .

Сжижение газов

Пусть необходимо охладить идеальный газ путём отведения тепла в область с более высокой температурой. Тогда наименьшая затрачиваемая работа будет происходить по циклу Карно в обратном направлении (существование цикла с меньшей затрачиваемой работой противоречит второму закону термодинамики [31] ). Если получение сжиженного газа будет происходить непосредственно в рабочем теле, то идеальный цикл примет другой вид. Построим точки 0 и 1, на графике температуры-энтропии (T-S соответственно), так, чтобы они соответствовали одной температуре. Тогда в точках на участке 0-1 будет происходить конденсация газа [32] . Конденсированный газ будет удаляться из рабочего тела. В результате этого процесса переход с восстановлением газа будет невозможным [Комм 7] . Возможным же будет переход 1-2 [32] . В полученном цикле адиабатический процесс 3-0 выводит систему в точку, откуда возможна конденсация газа.

В реальном газе при наличии большого давления и низкой температуры возможна ситуация, когда значительную роль в движение молекул начинает играть межмолекулярное притяжение. В случае адиабатического расширения газа (например, в результате использования эффекта Джоуля — Томсона) из-за работы, которая тратится на преодоление межмолекулярного притяжения температура газа резко падает, часть газа конденсируется [33] . Адиабатическое дросселирование проходит с увеличением энтропии и не сразу после изотермического сжатия [32] .

Магнитное охлаждение

С помощью адиабатического размагничивания парамагнетиков можно достичь температуры в сотые доли Кельвина, а для некоторых веществ даже нанокельвинов. Метод был предложен Петером Дебаем и Уильямом Джиоком в 1926 году [34] . Парамагнитный образец для эффективного охлаждения должен иметь малую удельную теплоёмкость кристаллической решётки и большую удельную теплоёмкость магнитной подсистемы, его внутренние магнитные поля должны быть малы, а спин-решёточная связь достаточно сильной. Этим условиям удовлетворяют медь и сплав празеодима с никелем (PrNi₅) [35] .

При температуре порядка одного Кельвина спины электронов, как правило, упорядочены, в отличие от ядерных спинов I [36] . При этом связь между ядерными спинами различных атомов практически отсутствует. При магнитном охлаждении образец вначале намагничивают в сильном магнитном поле B (до нескольких Тл), которое упорядочивает его магнитную подсистему. Далее происходит адиабатическое размагничивание, которое сохраняет постоянной энтропию системы. Энтропия одного моля меди зависит от ядерных спинов I, поля B и температуры T (в Кельвинах) как

где R — газовая постоянная, b — внутреннее магнитное поле вещества, — магнетон Бора, а f(I) — некоторая функция от ядерного спина. В процессе, при котором энтропия остаётся постоянной, а магнитное поле B уменьшается, также уменьшается и температура образца T [34] [37] . Результирующая температура с учётом анизотропии фактора Ланде равна

где g и g₀ — факторы Ланде для направлений полей с напряжённостями H и H₀ соответственно [38] .

См. также

Примечания

Комментарии

1. ↑ Если в уравнении A считать работой внешних сил над системой, то уравнение будет иметь вид
2. ↑ Что можно наглядно проследить на этом рисунке, если наблюдать за любой помеченной красным молекулой
3. ↑ С. Карно показал, что двигатель с более высоким КПД позволил бы создать вечный двигатель см. Кудрявцев, 1956, с. 400-401
4. ↑ В соответствии с определением изотермический процесс происходит при постоянной температуре (см. например, Савельев, 2001, с 30). Если же процесс другой, то при постоянной температуре нагревателя/холодильника, очевидно в какой-то момент будет разность температур. Если же теплообмен происходит с телом переменной температуры, как в цикле Стирлинга, то это условие необязательно.
5. ↑ Чтобы соотвествовать циклу Отто, процесс сгорания топлива между вторым и третьим тактом должен быть быстрым по сравнению со временем такта.
6. ↑ Рабочая температура для дизельных двигателей, работающих по системе самовоспламенения, составляет 820-870K
7. ↑ Так как такой процесс будет сопровождаться передачей тепла между частями газа и, следовательно, будет необратимый (как любой процесс с передачей от более горячего тела к холодному — см. Савельев, 2001, с 106). А dS=0 для обратимого адиабатического процесса.

Источники

1. ↑ 123Кудрявцев, 1956, с. 396—399
2. ↑Савельев, 2001, с. 33-34
3. ↑Ландау, Лифшиц V, 1976, с. 55
4. ↑Кудрявцев, 1956, с. 185—186
5. ↑Савельев, 2001, с. 17
6. ↑ 1234Савельев, 2001, с. 30—32
7. ↑Сивухин, 1975, с. 54
8. ↑ 1234Савельев, 2001, с. 109—113
9. ↑ 123Савельев, 2001, с. 19—20
10. ↑ 12Ландау Л.Д., Ахиезер А.И., 1965, с. 181—182
11. ↑Ландау Л.Д., Ахиезер А.И., 1965, с. 196—198
12. ↑Савельев, 2001, с. 13
13. ↑Ландау, Лифшиц V, 1976, с. 56
14. ↑Ландау Л.Д., Ахиезер А.И., 1965, с. 185
15. ↑Ландау Л.Д., Ахиезер А.И., 1965, с. 196-198
16. ↑Ландау, Лифшиц V, 1976, с. 144
17. ↑White Frank M. Fluid Mechanics. — 4th. — McGraw-Hill, New York., 1998. — ISBN 978-0072281927
18. ↑Lange N. A. Lange’s Handbook of Chemistry. — 10th. — McGraw-Hill, New York., 1967. — P. 1524.
19. ↑ 12Адиабата // Большая советская энциклопедия.
20. ↑Сивухин, 1975, с. 78—79
21. ↑Ландау, Лифшиц V, 1976, с. 70
22. ↑ 12Глаголев К. В., Морозов А. Н.Применение термодинамических потенциалов для описания эффекта Джоуля-Томсона. Физическая термодинамика. МГТУ им. Н. Э. Баумана. Архивировано из первоисточника 1 февраля 2012.Проверено 4 января 2012.
23. ↑K. C. Pal Heat Power. — Orient Blackswan, 1990. — P. 85—88. — 480 p. — ISBN 9780861319596
24. ↑David R. Gaskell Introduction to the thermodynamics of materials. — 4th Ed. — Taylor & Francis, 2003. — P. 47. — 618 p. — ISBN 9781560329923
25. ↑ 12Савельев, 2001, с. 106
26. ↑ 123Савельев Т.4, 2001, с. 32—36
27. ↑Paul E. LyndorphWeather and Climate. — 3-е изд. — New Jersey: Rowman & Allanheld Publishers, 1985. — С. 95-97.
28. ↑Соболев В. В, Курс теоретической астрофизики. — 3-е изд. — М .: Наука, 1985. — С. 170-172. — 504 с.
29. ↑ 12Ландау Л.Д., Ахиезер А.И., 1965, с. 209
30. ↑ 12Кириллин, 2008
31. ↑Сивухин, 1975, с. 98—99
32. ↑ 123Сжижение газов // Большая советская энциклопедия.
33. ↑Адиабатный процесс // Большая советская энциклопедия.
34. ↑ 12Магнитное охлаждение — статья из Физической энциклопедии
35. ↑Anthony Kent Experimental low temperature physics. — Springer, 1993. — P. 141. — 212 p. — (Macmillan physical science). — ISBN 9781563960307
36. ↑Luke C. L., Wu Yan, Chien-Shieng Part B // Nuclear Physics. — Academic Press, 1963. — Vol. 5. — P. 187. — 886 p. — (Methods in Experimental Physics). — ISBN 9780124759459
37. ↑охлаждение/ Магнитное охлаждение — статья из Большой советской энциклопедии
38. ↑Luke C. L., Wu Yan, Chien-Shieng Part B // Nuclear Physics. — Academic Press, 1963. — Vol. 5. — P. 189. — 886 p. — (Methods in Experimental Physics). — ISBN 9780124759459

Литература

1. Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М .: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9
2. Савельев И. В. Курс общей физики:Волны. Оптика. — М .: Астрель, 2001. — Т. 4. — 256 с. — 7000 экз. — ISBN 5-17-004586-7
3. Ландау Л. Д., Ахиезер А. И., Лифшиц Е. М. Курс общей физики: Механика. Молекулярная физика. — М .: Наука, 1965.
4. Ландау Л. Д., Лифшиц Е. М. Статистическая физика Часть 1 // Теоретическая физика. — М .: Наука, 1976. — Т. V. — 584 с. — 45 000 экз.
5. Сивухин Д. В. Общий курс физики. — М .: МФТИ, 2005. — Т. I. Механика. — 560 с.
6. Сивухин Д. В. Общий курс физики. — М .: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
7. П. С. Кудрявцев История физики. — М .: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
8. В. А. Кириллин, В. В. Сычев, А. Е. ШейндлинТехническая термодинамика: учебник для вузов. — М .: Издательство МЭИ, 2008. — 496 с.

Эта статья входит в число хороших статей русскоязычного раздела Википедии.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Адиабатический процесс» в других словарях:

АДИАБАТИЧЕСКИЙ ПРОЦЕСС — (адиабатный процесс), процесс, при к ром физ. система не получает теплоты извне и не отдаёт её. А. п. протекают в системах, окружённых теплоизолирующей (адиабатной) оболочкой, но их можно реализовать и при отсутствии такой оболочки. Для этого… … Физическая энциклопедия

АДИАБАТИЧЕСКИЙ ПРОЦЕСС — АДИАБАТИЧЕСКИЙ ПРОЦЕСС, термодинамические изменения, при которых не происходит потеря или приращение тепла или массы в системе при сжатии или расширении газа и жидкости, входящих в систему. Истинный адиабатический процесс должен был бы… … Научно-технический энциклопедический словарь

адиабатический процесс — адиабатный процесс — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы адиабатный процесс EN adiabatic process … Справочник технического переводчика

АДИАБАТИЧЕСКИЙ ПРОЦЕСС — (от греч. adiabatos непереходимый), термодинамический процесс, при котором система не получает теплоты извне и не отдает ее. Экологический энциклопедический словарь. Кишинев: Главная редакция Молдавской советской энциклопедии. И.И. Дедю. 1989 … Экологический словарь

адиабатический процесс — Изменение термодинамического состояния воздушной массы, протекающее без обмена теплом с окружающей ее средой, противоположен диабатическому процессу … Словарь по географии

адиабатический процесс — (гр. adiabatos непроходимый) изменение состояния физ. тела без притока и отдачи тепла; играет важную роль в атмосфере. Новый словарь иностранных слов. by EdwART, , 2009. адиабатический процесс [от гр. непереходимый] – изменение состояния… … Словарь иностранных слов русского языка

адиабатический процесс — Смотри адиабатный (адиабатический) процесс … Энциклопедический словарь по металлургии

адиабатический процесс — adiabatinis vyksmas statusas T sritis Standartizacija ir metrologija apibrėžtis Termodinaminės sistemos būsenos kitimas, vykstąs be šilumos mainų su aplinka. atitikmenys: angl. adiabatic process vok. adiabater Prozess, m; adiabatischer Prozess,… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

адиабатический процесс — adiabatinis vyksmas statusas T sritis fizika atitikmenys: angl. adiabatic process vok. adiabatische Zustandsänderung, f; adiabatischer Prozeß, m rus. адиабатический процесс, m pranc. processus adiabatique, m; transformation adiabatique, f … Fizikos terminų žodynas

АДИАБАТИЧЕСКИЙ ПРОЦЕСС — – термодинамический процесс без теплообмена с окружающей средой … Палеомагнитология, петромагнитология и геология. Словарь-справочник.

Источник