Что значит абсолютно неупругое столкновение

Абсолютно неупругий удар

Уда́р — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.

Содержание

Физическая абстракция

Причины отказа механики
Прогиб
Коррозия
Пластическая деформация
Усталость материала
Удар
Трещина
Плавление
Износ

При ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии. Предполагается, что за время удара действием внешних сил можно пренебречь, тогда полный импульс тел при ударе сохраняется, в противном случае нужно учитывать импульс внешних сил. Часть энергии обычно уходит на нагрев тел.

Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара. Обычно рассматривают либо абсолютно упругий удар, либо вводят коэффициент сохранения энергии k, как отношение кинетической энергии после удара к кинетической энергии до удара при ударе одного тела о неподвижную стенку, сделанную из материала другого тела. Таким образом, k является характеристикой материала, из которого изготовлены тела, и (предположительно) не зависит от остальных параметров тел (формы, скорости и т. п.).

Если неизвестны потери энергии, происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначно движение тел после удара невозможно. В этом случае рассматривается зависимость возможных углов рассеяния и скоростей тел после удара от начальных условий. Например, при столкновении двух элементарных частиц рассеяние может произойти лишь в некотором диапазоне углов, определяющемся предельным углом рассеяния.

В общем случае задача о столкновении требует знания дополнительных параметров, кроме начальных скоростей.

Абсолютно упругий удар

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.

Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.

Абсолютно неупругий удар

Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

Реальный удар

При реальном ударе макроскопических тел происходит деформация соударяющихся тел и распространение по ним упругих волн, передающих взаимодействие от сталкивающихся границ по всему телу. Пусть сталкиваются одинаковые тела. Если c — скорость звука в теле, L — характерный размер каждого тела, то время удара будет порядка t = 2L / c . Множитель 2 соответствует распространению волны в прямом и обратном направлении. Соответственно, систему сталкивающихся тел можно считать замкнутой, если импульс внешних сил за время t мал по сравнению с импульсами тел. Кроме того, само время t должно быть достаточно мало, в противном случае становится проблематично оценить потери энергии на деформации за время удара (часть энергии всегда расходуется на внутреннее трение), а само описание сталкивающихся тел становится неполным из-за существенного вклада внутренних степеней свободы. Необходимо, чтобы все деформации при ударе были существенно меньше, чем размеры тел.

Источник

Упругие и неупругие соударения

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

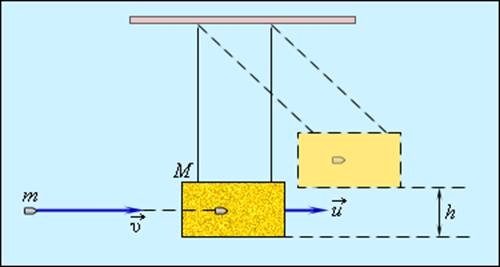
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.

Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса

При застревании пули в песке произошла потеря механической энергии:

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:

Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

При m > М) отношение

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:

где h – максимальная высота подъема маятника. Из этих соотношений следует:

Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

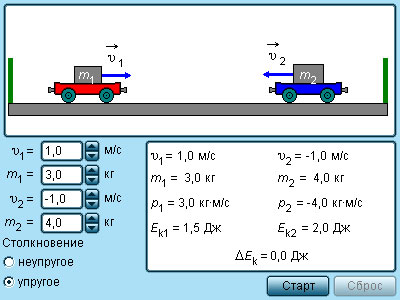
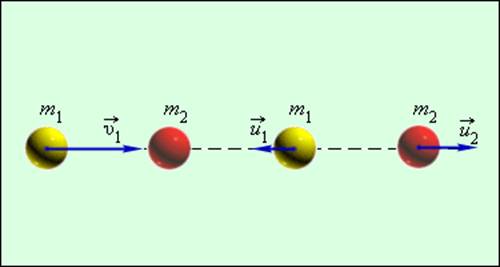
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

Абсолютно упругий центральный удар шаров

В общем случае массы m₁ и m₂ соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии

Здесь υ₁ – скорость первого шара до столкновения, скорость второго шара υ₂ = 0, u₁ и u₂ – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u₁ и u₂ шаров после столкновения:

В частном случае, когда оба шара имеют одинаковые массы (m₁ = m₂), первый шар после соударения останавливается (u₁ = 0), а второй движется со скоростью u₂ = υ₁, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ₂ ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ₂ относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ₁‘ = υ₁ – υ₂. Определив по приведенным выше формулам скорости u₁ и u₂ шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).

Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние

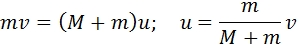
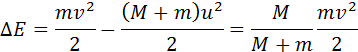
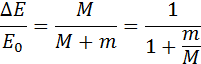
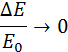
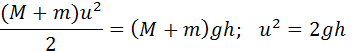
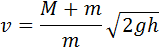
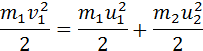
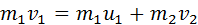
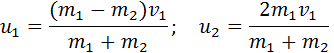
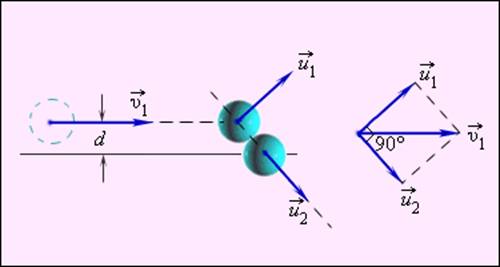
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и 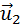после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости 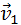налетающего шара. Если массы шаров одинаковы, то векторы скоростей и шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m₁ = m₂ = m эти законы принимают вид:

Первое из этих равенств означает, что векторы скоростей , и образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами и равен 90°.

Источник

Абсолютно упругий и абсолютно неупругий удар

Механическое взаимодействие в природе можно условно разделить на ударное и безударное.

Безударное взаимодействие – это притяжение и отталкивание.

Для ударного взаимодействия в задачах механики применяют закон сохранения импульса.

Виды ударов

В школьном курсе физики рассматривают два вида ударного взаимодействия: абсолютно упругий удар или абсолютно неупругий удар.

Если деформации тел при ударе нет, считают, что удар абсолютно упругий.

Если же деформация присутствует и после удара образуется новое тело – удар абсолютно неупругий.

Абсолютно упругий и абсолютно неупругий удары – это два крайних случая на шкале ударного взаимодействия

При ударах большинства реальных тел часть энергии всегда тратится на деформацию этих тел. Поэтому, удары большинства реальных тел лежат на шкале между двумя крайними видами ударов.

Рассмотрим движение тел вдоль одной прямой. Тела либо двигаются навстречу, либо одно тело догоняет другое.

Абсолютно неупругий удар

Суть абсолютно неупругого удара кратко можно описать так: Две капли ртути катились, ударились, слились в общую каплю ртути.

Нарисуем капли ртути до удара. Отметим на рисунке массу каждой капли. Скорости капель укажем с помощью векторов, направленных по движению каждой капли.

Нарисуем ось, для того, чтобы определить знак для импульса каждой капли.

Импульс, сонаправленный с осью, будет иметь положительный знак, направленный против оси – отрицательный.

Сложим векторы импульсов, чтобы найти общий импульс системы – вектор \(\vec>> \).

Каждый импульс запишем со своим знаком

Сделаем второй рисунок, описывающий ситуацию после абсолютно неупругого удара.

На этом рисунке укажем массу образовавшейся капли и ее скорость. Укажем стрелкой и символом \(\vec>> \), куда движется капля после удара .

Ось поможет выбрать знак для импульса капли.

На рисунке скорость сонаправлена с осью, поэтому, импульс капли после удара имеет положительный знак.

Примечание: Иногда в условии задачи не уточняется, в какую сторону будет двигаться тело после удара. В таком случае, направление движения выбираем сами (влево или вправо на рисунке). Если в ходе решения получим импульс тела, или его скорость со знаком минус, значит, тело движется в противоположную сторону от указанного нами направления. Такой выбор направления ошибкой считаться не будет. А знак минус подскажет, что импульс (и скорость) нужно развернуть в противоположную сторону.

Значит, закон сохранения импульса для абсолютно неупругого удара запишем в таком виде:

При абсолютно неупругом ударе:
— Выполняется закон сохранения импульса,
— Не выполняется закон сохранения энергии, так как часть энергии тратится на деформацию тел.

Примечание: Встречаются задачи вида: человек на льду бросил гирю в горизонтальном направлении, гиря полетела в одну сторону, а человек – в противоположную. Такие задачи решаем, применяя принципы для абсолютно неупругого удара. С той лишь разницей, что меняем местами рисунки до и после удара. Вначале тела находились вместе, после броска – разлетелись в противоположные стороны.

Абсолютно упругий удар

Кратко суть абсолютно упругого удара опишем так: Два бильярдных шара катились, без деформации ударились, и разбежались в разные стороны.

Составим рисунок для ситуации до удара. Отметим на рисунке массу каждого шара. Скорости шаров укажем с помощью векторов, направленных по движению каждого шара.

Запишем импульсы шаров до удара

Нарисуем ось, чтобы определить знаки импульсов каждого шара. Сонаправленный с осью импульс имеет знак «+», направленный против оси – знак «-».

Сложим импульсы и найдем общий импульс системы – вектор \(\vec>> \).

Каждый импульс записываем со своим знаком

На втором рисунке опишем задачу после абсолютно упругого удара.

Укажем массы шаров, их скорости нарисуем стрелками в направлении движения каждого шара. Обозначим скорости символами \(\vec>> \) и \(\vec>> \).

С помощью проведенной оси выбираем знаки импульсов шаров.

Составим выражение для общего импульса после удара.

Для замкнутой системы выполняется закон сохранения импульса

Запишем его в развернутом виде для абсолютно упругого удара:

При абсолютно упругом ударе:
— Выполняется закон сохранения импульса,
— Выполняется закон сохранения энергии.

Алгоритм решения задач на тему закон сохранения импульса

Решение большинства задач на закон сохранения импульса можно проводить по такому алгоритму:

1. Убеждаемся, что систем замкнутая. О видах систем написано тут.
2. На рисунке описываем ситуацию до удара.
3. Складываем импульсы всех тел системы до удара. Полученный вектор – это \( \vec>>\)
4. Составляем второй рисунок, на котором представляем ситуацию после удара.
5. Складываем импульсы всех тел системы после удара. Полученный вектор – это \( \vec>>\)
6. Приравниваем импульсы \( \vec>>\) до удара и \( \vec>>\) после удара

Если тела двигаются под углом друг к другу (вдоль непараллельных прямых)

При решении таких задач, нужно помнить, что, векторы \( \vec>>\) равны. Значит, когда нам известен один из векторов, автоматически становится известен и второй вектор.

Поэтому, когда нужно определить импульс тела в задачах, в которых тела не двигаются вдоль одной прямой, мы ищем тот импульс \( \vec>>\) , который нам удобнее найти. А после этого применяем тот факт, что векторы равны \( \vec>> = \vec>>\).

Источник