Что значит абсолютная погрешность округления

Приложение А. Погрешности вычислений

Абсолютная и относительная погрешности

Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.

Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:

(А.1)

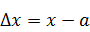
где а – приближенное значение числа х.

Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:

(А.2)

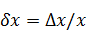
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность . В дальнейшем значение принимается в качестве абсолютной погрешности приближенного числа а. Тогда истинное значение х находится в интервале .

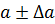
Источники погрешностей

Рассмотрим различные причины возникновения погрешностей.

Математическая модель задачи является неточной

Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).

Ошибки в исходных данных

Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.

Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.

Вычислительные ошибки (ошибки округления)

Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.

Вычислительные ошибки

Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.

Представление чисел с плавающей точкой

Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от .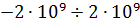

В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:

(А.3)

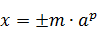
где m – мантисса, p – порядок, а – основание степени.

Мантисса записывается в нормализованной форме – с фиксированной точкой, подразумеваемой после первой значащей цифры. Нормализованной формой числа с плавающей точкой называется такая форма, в которой мантисса десятичного числа (без учёта знака) принимает значения , а мантисса двоичного числа принимает значения от .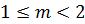

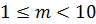
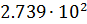
Например, число 273.9 можно представить в виде или в компьютерном представлении 2.739E+02.

В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.

Точность	Одинарная	Двойная
Размер (байты)	4	8
Наименьшее значение	1.2·10 −38	2.3·10 −308
Наибольшее значение	3.4×10 +38	1.7×10 +308
Размеры степени и мантиссы (биты)	8-23	11-52

Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой

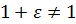
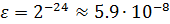
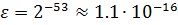
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что . Например, для числа с одинарной точностью 1 + 0.00000001 = 1. Для одинарной точности , а для двойной точности .

Погрешность округления

При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность принимается равной половине единицы последнего разряда числа. Например, значение могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом . При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.

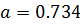
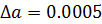
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:

Погрешность арифметических действий над приближенными числами

При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:

, (А.4)

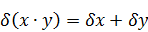
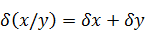
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:

(А.5)

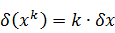
При сложении или вычитании чисел их абсолютные погрешности складываются:

(А.6)

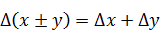
Относительная погрешность суммы положительных слагаемых вычисляется как:

. (А.7)

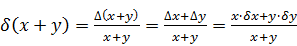
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

. (А.8)

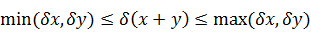
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность .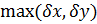

При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:

1234 + 0.005678 = 1234.00005678

или в компьютерном представлении:

1.234Е+03 + 5.678Е-03 = 1.234005678Е+03

После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.

Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 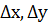результат их сложения в знаменателе может быть очень малым. Чтобы уменьшить погрешность при вычитании, необходимо строить вычислительные алгоритмы таким образом, чтобы избегать вычитания близких чисел.

Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.

Источник

Абсолютная погрешность и ее граница

Вычислительная математика. Абсолютная погрешность

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.

ЗАПИСЬ ПРИБЛИЖЕННОГО ЧИСЛА.

ВЕРНЫЕ И ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА

х – точное число

а – приближенное число

Разность х – а между точным числом х и приближенным числом а называется погрешностью приближения.

Модуль погрешности называется абсолютной погрешностью и обозначается ∆:

Погрешность и абсолютная погрешность имеют ту же размерность, что и рассматриваемая величина

Граница абсолютной погрешности ∆а – положительное число, которое больше или равно абсолютной погрешности или:

Если задана граница абсолютной погрешности ∆а, то число а есть приближенное значение числа х с точностью до ∆а и записывают

х = а ± ∆а, например: 94,5 ± 0,3

В отличие от абсолютной погрешности, граница абсолютной погрешности не определяется однозначно, поэтому на практике выбирается такое значение границы абсолютной погрешности, которое удобно для вычислений и обеспечивает максимальную точность.

Цифра приближенного числа а, записанного в виде десятичной дроби, называется верной (точной), если граница абсолютной погрешности числа не превышает (меньше или равно) единицы того разряда, в котором стоит эта цифра. В противном случае она называется сомнительной, например:

Граница погрешности 0,2 , поэтому рассмотрим

цифру 5, разряд единицы, единица разряда 1 и 0,2

Цифра 6, разряд десятые, единица разряда 0,1 и 0,2 > 0,1 (граница погрешности превышает единицу разряда), значит цифра 6 – сомнительная. Значит и цифра 3 (сотые) будет также сомнительной

2 и 5 – верные цифры, 6 и 3 – сомнительные цифры числа

Запись чисел с сохранением только верных цифр широко используется во всех математических таблицах, в справочниках (физика, астрономия, техника). При этом, по записи приближенного числа можно оценить погрешность приближения, например:

табличные данные: температура кипения золота – 2700 ºС, значит граница абсолютной погрешности 1 ºС, температура кипения йода – 182,8 ºС, значит граница абсолютной погрешности 0,1 ºС.

Записи приближенных чисел 0,3; 0,30; 0,300 – неравносильны, т.к. приближенное число 0,3 имеет погрешность не более 0,1;

приближенное число 0,30 имеет погрешность не более 0,01;

приближенное число 0,300 имеет погрешность не более 0,001.

Если целое число содержит в конце нули, не являющиеся верными цифрами, то их заменяют множителем 10 р , где р – число таких нулей.

В записи приближенных чисел принято соблюдать следующие правила:

• Оставлять в записи приближенного числа только верные цифры;
• Если в десятичной дроби последние верные цифры нули, то их надо выписать;
• Если число содержит в конце нули, не являющиеся верными цифрами, то они должны быть заменены на 10 р , где р – число нулей, которые надо заменить

Записать правильно следующие приближенные числа:

1. а = 0,075 ± 0,000005 – здесь погрешность меньше, чем 0,00001 (0,000005
2. а = 746000000 ± 5000 здесь погрешность меньше, чем 10000 (5000 р а = 74600·10 4
3. а = 0,35 ∆а = 0,00005 – здесь погрешность меньше, чем 0,0001 значит

а = 0,3500 (последние верные цифры нули)

1. а = 765000 ∆а = 5 – здесь погрешность 5
2. а = 0,3700 ∆а = 0,05 – здесь погрешность 0,05

В некоторых заданиях необходимо наоборот определить абсолютную погрешность по записи приближенного числа, например,

Указать абсолютную погрешность приближенных чисел:

1. а = 14,5 ·10, значит ∆а = 10
2. а = 34,20 т.к. последний нуль является верной цифрой, то ∆а = 0,01
3. а = 263·10 4 , значит ∆а = 10000

Число в стандартном виде записывают так:

показатель m – называется порядком числа.

Если число, записанное в виде десятичной дроби содержит все верные цифры, то все его цифры, начиная с первой слева отличной от нуля, называют значащими, например:

7,03 – три значащие цифры

4400 – четыре значащие цифры

0,000270 – три значащие цифры (нули, расположенные левее первой, отличной от нуля цифры, не считаются значащими 0,000270).

Округление числа – это замена его числом с меньшим количеством значащих цифр. При округлении числа до m значащих цифр отбрасывают все цифры, стоящие правее m-ой значащей цифры, заменяя их на нули (при сохранении разряда). При этом, если первая из отбрасываемых цифр ≥ 5, то последнюю оставшуюся цифру увеличивают на единицу,

Округлить число с заданной точностью:

• с точностью до 10 -3 (10 -3 = 0,001)

Значащие цифры – 1, 5, 7 и 8, цифра 3 – сомнительная, т.к. 0,001 > 0,0001 (единицы разряда)

1,5783 ≈ 1,578 (последняя из отбрасываемых цифр 3

Значащие цифры – 2, 3, 4, 9 и 9, цифра 7 – сомнительная

7>5, значит предыдущую увеличиваем на 1, получим

• с точностью до 10 -2 (10 -2 = 0,01)

• с точностью до 10 3 (10 3 = 1000)

159734 ≈ 160000 = 160·10 3

28,34 ≈ 0 – ни одна из цифр не является значащей 1000 > 10, т.к. задана точность 1000, а заданное число меньше, чем погрешность.

Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие)

Источник